Алгоритмы сортировки: сортировка слиянием в Golang 

Сортировка слиянием — очень популярный алгоритм сортировки. Он основан на подходе «разделяй и властвуй», т.е. в этом алгоритме вы делите массив на две равные половины, пока каждая половина не будет содержать только один элемент. После разделения массива вы начинаете рекурсивно объединять их, пока не получите отсортированный массив.

Вот пример, демонстрирующий рабочий подход к сортировке слиянием:

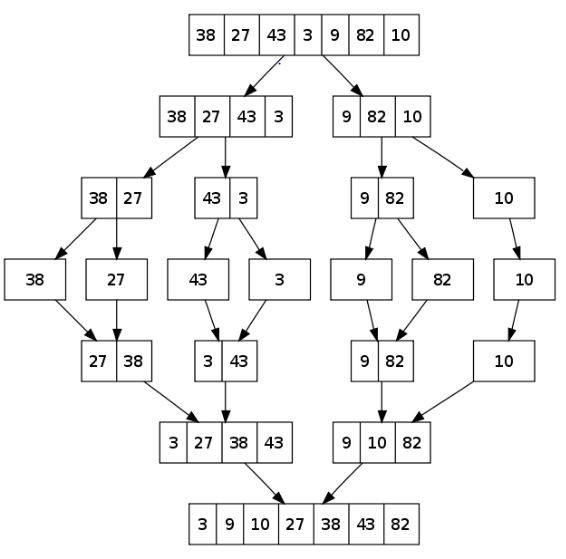
Реализация сортировки слиянием в Go

Мы пишем код для сортировки слиянием, используя рекурсию, которую мы называем сортировкой слиянием, пока каждая половина не будет состоять из одного элемента. Когда каждая половина имеет один элемент, мы вызываем операцию слияния, чтобы объединить два несортированных массива, пока не получим полный отсортированный массив. В операции слияния нам дается начальный, средний и последний индекс двух несортированных массивов, мы создаем два массива с именами левый и правый подмассивы и начинаем их объединять. Пространственная сложность операции слияния составляет O(n), так как нам требуется место для левого и правого подмассива. Временная сложность операции слияния также составляет O(n), поскольку мы запускаем цикл for до длины массива.

package main
import "fmt"
func Merge_sort(A *[]int,start int,last int){
    if start<last{
       mid :=(start+last)/2
       fmt.Printf("mid is:%d",mid)
       Merge_sort(A, start, mid)
       Merge_sort(A,mid+1,last)
       Merge(A,start,mid,last)
       PrintArr(A)
    }
}
func Merge(A *[]int,start,mid,last int){
   n1:=mid-start+1
   n2:=last-mid
   l:=make([]int,n1 )
   r:= make([]int, n2)
   for i:=0;i<n1;i++{
     l[i] = (*A)[start+i]
   }
   for j:=0;j<n2;j++{
     r[j] = (*A)[mid+1+j]
   }
   i:=0
   j:=0
   k:=start
   for i<n1 && j<n2{
     if l[i]<r[j]{
        (*A)[k] =l[i]
        i++
        k++
     }else{
        (*A)[k]=r[j]
         j++
         k++
     }
  }
  for i==n1 &&j<n2{
     (*A)[k] = r[j]
      j++
      k++
  }
  for j==n2 &&i<n1{
     (*A)[k] = l[i]
      i++
      k++
  }
}
func PrintArr(A *[] int){
    for i:=0; i<len(*A);i++{
       fmt.Printf("A[%d]:%d\n", i ,(*A)[i])
    }
}
func main(){
    A:=[]int{38,27,43,3,9,82,10}
    Merge_sort(&A, 0,(len(A)-1))
    fmt.Printf("Array after merge sort:\n")
    PrintArr(&A)
}

Сортировка слиянием — это неуместный алгоритм, поскольку он использует дополнительное пространство памяти в операции слияния для сортировки. Это алгоритм внутренней сортировки, поскольку он не меняет порядок сходных элементов. Временная сложность алгоритма сортировки слиянием составляет O(n * log (n)), поскольку операция слияния называется временем O(log (n)). Пространственная сложность сортировки слиянием составляет O (n) [(O (n) (из-за операции слияния) + O (log (n)) (из-за пространства стека, используемого для рекурсии) = O (n)].