Бинарное дерево 3.0

В моей предыдущей статье мы погрузились в мир иерархических структур данных и обсудили важность алгоритмов поиска и сортировки, а также алгоритмов обхода. Теперь в этой статье мы сосредоточимся на менее известных приложениях двоичных деревьев. Мы рассмотрим их исключительную полезность в алгоритмах криптографии и оптимизации. Криптография обеспечивает безопасную передачу и хранение информации, а двоичные деревья играют решающую роль в различных криптографических алгоритмах. Кроме того, бинарные деревья служат мощным инструментом оптимизации, помогая находить оптимальные решения в сложных задачах. Присоединяйтесь к нам, чтобы открыть для себя захватывающий мир двоичных деревьев в сфере криптографии и оптимизации.
Криптография и структуры данных безопасности
Структуры данных играют важнейшую роль в криптографии и безопасности, обеспечивая основу для безопасного хранения, обработки и защиты конфиденциальной информации. В этих областях специальные структуры данных предназначены для обеспечения конфиденциальности, целостности и подлинности данных.
Системы управления ключами используют сложные структуры данных для безопасного хранения криптографических ключей и управления ими. Деревья ключей, кольца ключей или хранилища ключей используются для организации и защиты ключей, реализации контроля доступа и механизмов шифрования для обеспечения их конфиденциальности и целостности.
Хэш-таблицы широко используются в приложениях безопасности для эффективного хранения и поиска данных. Они являются неотъемлемой частью хеширования и проверки паролей, где хешированные пароли хранятся в хеш-таблице для быстрого сравнения во время аутентификации. Хэш-таблицы также используются для быстрого поиска в списках управления доступом, таблицах маршрутизации и списках отзыва цифровых сертификатов.
Деревья Меркла, также известные как хеш-деревья, представляют собой бинарные деревья, обеспечивающие эффективную проверку целостности данных и обнаружение несанкционированного доступа. Они широко используются в криптографических протоколах, таких как технология блокчейн, для обеспечения целостности больших структур данных. Деревья Меркла используют криптографические хэш-функции для суммирования данных на разных уровнях, при этом корневой хеш представляет общую целостность структуры данных.
Безопасные многосторонние вычисления (MPC) основаны на определенных структурах данных, обеспечивающих безопасное сотрудничество между несколькими сторонами. Схемы совместного использования секретов делят конфиденциальные данные на доли, распределяемые между участниками, что позволяет выполнять вычисления без раскрытия отдельных входных данных. Искаженные каналы и методы передачи данных без ведома дополнительно защищают конфиденциальность и обеспечивают безопасность вычислений в многопользовательских настройках.
Списки контроля доступа (ACL) — это фундаментальные структуры данных в системах безопасности. Они определяют разрешения и привилегии, связанные с различными сущностями, обеспечивая детальное управление доступом. ACL определяют, кто может получить доступ к ресурсам и какие действия они могут выполнять, обеспечивая авторизованное и безопасное взаимодействие внутри системы.
В сфере инфраструктуры открытых ключей (PKI) цифровые сертификаты и цепочки сертификатов являются важными структурами данных. Цифровые сертификаты связывают открытые ключи с идентификационной информацией и цифровыми подписями, устанавливая доверие и проверяя подлинность объектов. Цепочки сертификатов, также известные как иерархии сертификатов, создают иерархическую структуру сертификатов для установления доверительных отношений. Они позволяют проверять всю цепочку доверия, обеспечивая целостность и подлинность цифровых сертификатов.
Эти структуры данных составляют основу криптографии и систем безопасности, упрощая безопасное хранение, манипулирование и контроль доступа к конфиденциальной информации. Используя эти структуры, организации могут защищать конфиденциальность данных, обеспечивать целостность данных, устанавливать доверие и обеспечивать безопасные вычисления, способствуя созданию надежных и надежных архитектур безопасности.
1. Системы и структуры управления ключами в криптографии и безопасности
Системы управления ключами являются важнейшими компонентами криптографии и безопасности, обеспечивая основу для безопасного хранения, распространения и управления криптографическими ключами. Криптографические ключи необходимы для шифрования, дешифрования, цифровых подписей и других криптографических операций. Надежная система управления ключами обеспечивает конфиденциальность, целостность и доступность криптографических ключей на протяжении всего их жизненного цикла.
Системы управления ключами обычно используют иерархическую структуру для организации и защиты криптографических ключей. Одной из часто используемых структур является дерево ключей, которое напоминает иерархическую древовидную структуру. В корне дерева находится главный ключ или ключ шифрования ключей (KEK). KEK используется для шифрования и расшифровки других ключей в системе. Дерево разветвляется на подразделы, каждый из которых служит определенной цели, такой как шифрование данных, аутентификация или безопасная связь.
Другим подходом является структура кольца для ключей, в которой ключи сгруппированы в логические блоки, называемые кольцами для ключей. Брелоки позволяют легко управлять и администрировать ключи с различными целями или уровнями доступа. Каждое кольцо для ключей может содержать несколько ключей, а средства контроля доступа могут применяться на уровне кольца для ключей, чтобы обеспечить надлежащую авторизацию для использования ключей.
Кроме того, хранилища ключей обеспечивают безопасное хранилище криптографических ключей. Хранилища ключей предлагают расширенные механизмы защиты, такие как контроль доступа, шифрование и обнаружение несанкционированного доступа для защиты ключей. Эти хранилища могут быть реализованы в виде аппаратных модулей безопасности (HSM) или программных решений. Аппаратные хранилища ключей обеспечивают дополнительную физическую безопасность за счет хранения ключей в защищенных от несанкционированного доступа аппаратных устройствах.
Системы управления ключами также включают различные функции безопасности для защиты криптографических ключей. Управление жизненным циклом ключей обеспечивает безопасное создание ключей, их периодическую ротацию и безопасное уничтожение, когда они больше не нужны. Элементы управления доступом реализованы для ограничения доступа к ключам авторизованным лицам или системам. Журналы аудита и механизмы регистрации отслеживают использование ключей и помогают обнаруживать любые подозрительные действия.
Кроме того, методы шифрования часто используются для защиты самих ключей. Ключи шифрования ключей (KEK) используются для шифрования и дешифрования других ключей, добавляя дополнительный уровень защиты. Алгоритмы упаковки ключей защищают передачу или хранение ключей, шифруя их с помощью KEK или других ключей упаковки.
В целом, системы управления ключами играют жизненно важную роль в поддержании безопасности и эффективности криптографических операций. Они обеспечивают структурированную основу для создания, хранения, распространения и защиты криптографических ключей на протяжении всего их жизненного цикла. Используя иерархические структуры, средства управления доступом, методы шифрования и безопасные механизмы хранения, системы управления ключами обеспечивают конфиденциальность, целостность и доступность криптографических ключей в криптографии и приложениях безопасности.
Вот пример реализации системы управления ключами с использованием двоичного дерева:
class KeyNode {
key: string;
left: KeyNode | null;
right: KeyNode | null;
constructor(key: string) {
this.key = key;
this.left = null;
this.right = null;
}
}
class KeyManagementSystem {
root: KeyNode | null;
constructor() {
this.root = null;
}
insert(key: string): void {
const newNode = new KeyNode(key);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
private insertNode(node: KeyNode, newNode: KeyNode): void {
if (newNode.key < node.key) {
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
search(key: string): boolean {
return this.searchNode(this.root, key);
}
private searchNode(node: KeyNode | null, key: string): boolean {
if (node === null) {
return false;
}
if (key === node.key) {
return true;
} else if (key < node.key) {
return this.searchNode(node.left, key);
} else {
return this.searchNode(node.right, key);
}
}
}В этом примере класс KeyNode представляет узел в двоичном дереве, где каждый узел содержит значение ключа. Класс KeyManagementSystem действует как система управления ключами, используя структуру двоичного дерева для хранения ключей и управления ими.
Метод insert позволяет вставлять ключи в двоичное дерево. Частный метод insertNode вызывается рекурсивно, чтобы найти подходящую позицию для вставки нового ключевого узла на основе сравнения значения ключа.
Метод search позволяет искать определенный ключ в двоичном дереве. Частный метод searchNode рекурсивно вызывается для обхода дерева и поиска соответствующего ключа.
Пример использования демонстрирует вставку ключей в систему управления ключами и поиск определенных ключей. Выводит true, если ключ найден, и false, если ключа нет в системе.
2. Деревья Меркла и их структура в криптографии и безопасности
Деревья Меркла, также известные как хэш-деревья, представляют собой фундаментальную криптографическую структуру данных, которая обеспечивает эффективную проверку целостности данных и обнаружение несанкционированного доступа. Они играют решающую роль в обеспечении надежности и безопасности данных в различных приложениях, включая технологию блокчейн, распределенные файловые системы и безопасные протоколы связи.
Деревья Меркла — это бинарные деревья, в которых каждый конечный узел представляет блок данных или хэш-значение блока данных. Древовидная структура строится путем рекурсивного хеширования пар дочерних узлов до тех пор, пока не будет получен единственный корневой хэш, известный как корень Меркла. Эта иерархическая структура позволяет эффективно проверять целостность данных даже для больших наборов данных.
Ключевая идея деревьев Меркла заключается в том, что изменения в любом блоке данных внутри дерева распространяются до корня. Это свойство обеспечивает быстрое обнаружение измененных или поврежденных блоков данных без необходимости просмотра всего набора данных. Сравнивая вычисленный корневой хэш с доверенным или общедоступным хэшем, можно эффективно проверить целостность всего набора данных.
Пожалуйста, не путайте эти два:
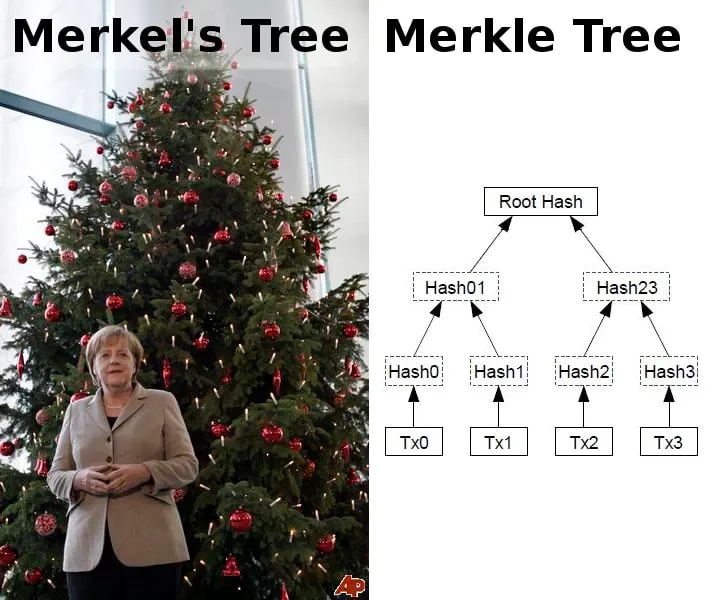
Чтобы проверить целостность определенного блока данных, участнику необходимо иметь доступ к корню Merkle и подмножеству хеш-значений, известному как путь Merkle. Путь Меркла состоит из хеш-значений от листового узла до корневого узла, включая соответствующие хэши-сестры вдоль пути. Пересчитав и сравнив вычисленные хэш-значения с предоставленным путем и корнем Меркла, можно проверить, не изменился ли блок данных или произошло какое-либо вмешательство.
Деревья Меркла предлагают несколько преимуществ в криптографических приложениях. Во-первых, они обеспечивают масштабируемый и эффективный способ проверки целостности больших наборов данных, поскольку процесс проверки требует только логарифмической временной сложности. Во-вторых, деревья Меркла обеспечивают повышенную безопасность, поскольку фальсификация даже одного блока данных приведет к другому корневому хэшу, который можно легко обнаружить во время проверки. Это свойство гарантирует, что любые несанкционированные изменения данных будут немедленно обнаружены.
Деревья Меркла находят широкое применение в различных криптографических протоколах и системах. В технологии блокчейн деревья Меркла используются для проверки целостности транзакций и блоков, что позволяет участникам эффективно проверять согласованность блокчейна, не требуя всей истории транзакций. В распределенных файловых системах деревья Меркла используются для обеспечения целостности файловых блоков, что обеспечивает эффективную проверку данных и исправление ошибок. Они также используются в протоколах защищенной связи для проверки целостности сообщений, гарантируя, что передаваемые данные останутся неизменными во время передачи.
Таким образом, деревья Меркла — это мощные структуры данных, обеспечивающие эффективную и надежную проверку целостности блоков данных. Благодаря своей иерархической структуре и распространению изменений корневого хэша они обеспечивают обнаружение несанкционированного доступа и целостность данных в различных криптографических приложениях. Используя деревья Меркла, организации могут обеспечить достоверность и надежность своих данных, укрепив основы безопасности систем блокчейна, распределенных файловых систем и безопасных протоколов связи.
Вот пример реализации дерева Меркла:
import * as CryptoJS from 'crypto-js';
class MerkleTree {
tree: string[][];
constructor(leaves: string[]) {
this.tree = [leaves];
this.buildTree();
}
buildTree(): void {
let layerIndex = 0;
while (this.tree[layerIndex].length > 1) {
this.tree.push(this.createNextLayer(this.tree[layerIndex]));
layerIndex++;
}
}
contains(hash: string): boolean {
for (let layer of this.tree) {
for (let node of layer) {
if (node === hash) {
return true;
}
}
}
return false;
}
createNextLayer(nodes: string[]): string[] {
let nextLayer: string[] = [];
let layerSize = nodes.length;
for (let i = 0; i < layerSize; i += 2) {
if (i + 1 < layerSize) {
let combined = this.combine(nodes[i], nodes[i + 1]);
nextLayer.push(this.hash(combined));
} else {
// In case of an odd number of nodes, the last node is repeated
let combined = this.combine(nodes[i], nodes[i]);
nextLayer.push(this.hash(combined));
}
}
return nextLayer;
}
combine(a: string, b: string): string {
return a + b;
}
hash(value: string): string {
return CryptoJS.SHA256(value).toString();
}
get root(): string {
return this.tree[this.tree.length - 1][0];
}
}
const leaves = ['a', 'b', 'c', 'd'].map(el => CryptoJS.SHA256(el).toString());
const merkleTree = new MerkleTree(leaves);
const aHash = CryptoJS.SHA256('a').toString();
console.assert(merkleTree.contains(aHash), 'Tree should contain hash of "a"');
const bHash = CryptoJS.SHA256('b').toString();
console.assert(merkleTree.contains(bHash), 'Tree should contain hash of "b"');
const notExistingHash = CryptoJS.SHA256('not existing').toString();
console.assert(!merkleTree.contains(notExistingHash), 'Tree should not contain hash of "not existing"');
console.assert(merkleTree.tree.length === 3, 'Tree should have 3 layers');
console.assert(merkleTree.tree[0].length === 4, 'Bottom layer should have 4 nodes');
console.assert(merkleTree.tree[1].length === 2, 'Middle layer should have 2 nodes');
console.assert(merkleTree.tree[2].length === 1, 'Top layer should have 1 node');
console.log("All tests passed!");
console.log(merkleTree.root);Этот фрагмент кода описывает реализацию двоичного дерева Меркла, фундаментальной структуры данных, используемой в криптографических системах и технологиях блокчейна. Дерево Меркла обеспечивает эффективную и безопасную проверку содержимого в больших структурах данных.
Реализация начинается с импорта библиотеки CryptoJS, предоставляющей основные криптографические функции, включая алгоритм хеширования SHA-256, используемый во всем коде.
Основная логика инкапсулирована в классе MerkleTree, который поддерживает древовидную структуру и связанные с ней методы. При создании экземпляра конструктор класса принимает массив предварительно хешированных листовых узлов. Узлы помещаются в переменную дерева и вызывается buildTree(), чтобы начать построение дерева.
Функция buildTree() работает итеративно, создавая дерево Меркла слой за слоем. Начиная с нижнего слоя (хэшированные входные значения), каждая пара значений объединяется и хэшируется для создания следующего слоя в дереве. Когда количество узлов на слое нечетное, последний узел дублируется перед этапом объединения и хеширования. Эта процедура повторяется до тех пор, пока не останется только один узел (корневой узел).
Функция contains() служит методом обхода дерева, проверяя дерево, чтобы проверить, включено ли в него конкретное хэшированное значение. В то время как функция createNextLayer() помогает операции buildTree(), принимая массив хешированных значений из текущего слоя и возвращая массив объединенных и хешированных пар для формирования следующего слоя.
Функция hash() воплощает простоту, обеспечивая прямое применение алгоритма SHA-256 к входному значению. Кроме того, включен метод получения root() для извлечения самого верхнего значения дерева, корневого хэша.
Следуя определению класса MerkleTree, экземпляр создается с использованием массива хешированных строковых значений. Впоследствии запускается несколько тестовых случаев, чтобы подтвердить правильность построения дерева и включение определенных значений в дерево. Результаты этих утверждений затем регистрируются на консоли. Наконец, распечатывается корень дерева Меркла, иллюстрирующий успешное построение дерева.
Оптимизация алгоритма
Оптимизация алгоритмов играет решающую роль в повышении производительности и эффективности алгоритмов, а бинарные деревья представляют собой общую структуру данных, к которой можно применять методы оптимизации. Двоичные деревья предлагают иерархическую структуру, которую можно использовать для улучшения таких операций, как поиск, вставка, удаление и обход. Используя различные стратегии оптимизации, мы можем оптимизировать алгоритмы, использующие бинарные деревья, чтобы сократить использование ресурсов, сократить время выполнения и улучшить масштабируемость.
Одним из ключевых аспектов оптимизации алгоритмов с помощью бинарных деревьев является обеспечение баланса дерева. Несбалансированные деревья могут привести к неэффективным операциям, особенно в случаях, когда дерево вырождается в связанный список. Такие методы, как деревья AVL или красно-черные деревья, могут использоваться для поддержания баланса двоичного дерева, гарантируя, что операции имеют оптимальную временную сложность. Балансировка дерева может значительно повысить эффективность таких операций, как поиск, вставка и удаление, за счет минимизации высоты дерева и обеспечения его относительной сбалансированности.
Другой важной областью оптимизации являются алгоритмы обхода, используемые для исследования бинарного дерева. Рекурсивный обход бинарного дерева, хотя и интуитивно понятный, может привести к снижению производительности из-за накладных расходов на вызов функций и использования стека. Методы оптимизации обхода включают использование итерационных методов вместо рекурсии, использование хвостовой рекурсии или обхода на основе цикла, а также минимизацию ненужных операций или проверок во время обхода. Эти оптимизации могут повысить эффективность алгоритмов обхода, таких как обходы по порядку, в предварительном и последующем порядке, что позволяет ускорить обработку элементов дерева.
Кэширование или мемоизация — еще один метод оптимизации, применимый к алгоритмам двоичного дерева. Идентифицируя повторяющиеся вычисления, кэширующие или мемо-таблицы могут хранить результаты дорогостоящих или часто выполняемых операций. Последующие вызовы той же операции могут затем получить кэшированный результат, избегая избыточных вычислений и значительно повышая общую производительность алгоритма. Кэширование особенно полезно в сценариях, где алгоритм двоичного дерева включает повторяющиеся вычисления, такие как динамическое программирование или определенные алгоритмы поиска.
Методы обрезки могут использоваться для удаления ненужных ветвей или поддеревьев во время обхода бинарного дерева. Тщательно анализируя требования задачи, можно определить условия, при которых можно пропустить целые поддеревья. Эта оптимизация уменьшает количество ненужных операций, что приводит к повышению производительности. Методы обрезки особенно эффективны при поиске определенных значений или алгоритмов оптимизации, таких как альфа-бета-отсечение в игровых деревьях, где большие части дерева могут быть удалены в зависимости от определенных условий.
Эффективное управление памятью имеет решающее значение при оптимизации алгоритмов, использующих бинарные деревья. Для повторного использования памяти можно использовать такие методы, как объединение объектов в пул, вместо постоянного выделения и освобождения узлов дерева. Это уменьшает фрагментацию памяти и улучшает использование памяти, что приводит к повышению общей производительности. Кроме того, можно исследовать оптимизированные по пространству представления двоичных деревьев, например, с использованием массивов или методов обработки битов, для более компактного представления древовидной структуры. Эти представления уменьшают нагрузку на память и могут повысить производительность кэша, особенно в сценариях, где использование памяти является критическим фактором.
Давайте рассмотрим некоторые практические случаи, когда эти алгоритмы могут быть необходимы.
1. GPS-навигация и бинарные деревья: повышение эффективности планирования маршрута
Системы GPS-навигации произвели революцию в способах навигации и путешествий, сделав эффективное планирование маршрута важнейшим аспектом этих систем. Двоичные деревья играют важную роль в оптимизации алгоритмов планирования маршрута, используемых в приложениях GPS-навигации, обеспечивая эффективную и точную навигацию из одного места в другое.
Планирование маршрута в GPS-навигации включает в себя поиск наиболее оптимального пути между начальной точкой и пунктом назначения с учетом различных факторов, таких как расстояние, условия движения и время в пути. Двоичные деревья обеспечивают иерархическую структуру, которую можно использовать для повышения эффективности этих алгоритмов.
Один из подходов заключается в использовании двоичного дерева поиска (BST) для хранения данных о местоположении. В BST каждый узел представляет географическое положение, а дерево организовано на основе порядка этих местоположений. Это позволяет эффективно выполнять операции поиска, чтобы найти ближайшее местоположение или местоположение с определенными атрибутами, например заправочную станцию или ресторан. Используя свойство бинарного поиска, системы GPS-навигации могут быстро находить близлежащие достопримечательности или определять следующий поворот на основе текущего местоположения пользователя.
Еще одно применение бинарных деревьев в GPS-навигации — представление самой дорожной сети. Каждый узел в бинарном дереве может представлять собой перекресток или точку дорожной сети. Затем дочерние узлы представляют возможные направления или дороги, ведущие от этого перекрестка. Эта иерархическая структура обеспечивает эффективное планирование маршрута путем обхода дерева от начальной точки до конечной с учетом доступных вариантов дорог на каждом перекрестке. Алгоритмы, такие как алгоритм Дейкстры или поиск A *, могут использоваться для поиска кратчайшего или самого быстрого пути через представление дорожной сети в виде двоичного дерева.
Эффективная навигация также требует обработки информации о дорожном движении в режиме реального времени. Двоичные деревья можно использовать для хранения и обновления данных о дорожном движении, таких как пробки на дорогах или аварии. Интегрируя эту информацию в представление дорожной сети в виде двоичного дерева, навигационные системы GPS могут динамически корректировать рекомендации по маршруту в зависимости от текущих условий движения. Это позволяет пользователям избегать перегруженных районов и выбирать альтернативные маршруты для более быстрого и эффективного перемещения.
Кроме того, бинарные деревья обеспечивают эффективное хранение и поиск картографических данных. Географические данные, включая карты, дорожные сети и достопримечательности, могут быть организованы и проиндексированы с помощью двоичных деревьев. Эта индексация обеспечивает быстрый доступ к соответствующим данным карты во время планирования маршрута и навигации.
Таким образом, навигационные системы GPS используют бинарные деревья для повышения эффективности алгоритмов планирования маршрута. Используя бинарные деревья поиска для данных о местоположении, представляя дорожные сети в виде бинарных деревьев, интегрируя информацию о трафике в реальном времени и организуя картографические данные с помощью индексации бинарного дерева, навигационные системы GPS могут обеспечивать точную и эффективную навигацию. Эти оптимизации гарантируют, что пользователи смогут находить наиболее оптимальные маршруты, экономить время и принимать обоснованные решения при перемещении из одного места в другое.
class TreeNode {
locationName: string;
distance: number;
left: TreeNode | null;
right: TreeNode | null;
constructor(locationName: string, distance: number) {
this.locationName = locationName;
this.distance = distance;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
root: TreeNode | null;
constructor() {
this.root = null;
}
insert(locationName: string, distance: number): void {
let newNode = new TreeNode(locationName, distance);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
insertNode(node: TreeNode, newNode: TreeNode): void {
if (newNode.distance < node.distance) {
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
findClosestLocation(distance: number): TreeNode | null {
let current = this.root;
let closest = this.root;
while(current !== null) {
if (Math.abs(current.distance - distance) < Math.abs(closest.distance - distance)) {
closest = current;
}
current = distance < current.distance ? current.left : current.right;
}
return closest;
}
}
let locationsTree = new BinarySearchTree();
locationsTree.insert('A', 10);
locationsTree.insert('B', 20);
locationsTree.insert('C', 15);
locationsTree.insert('D', 25);
let closestLocation = locationsTree.findClosestLocation(16);
if (closestLocation !== null) {
console.log(closestLocation.locationName);
}2. Оптимизация сети: максимальная эффективность и производительность
Оптимизация сети является важной областью компьютерных сетей, которая направлена на максимальное повышение эффективности и производительности сетей. Он включает в себя различные методы и подходы для улучшения потока данных, уменьшения задержки, минимизации перегрузки и оптимизации использования ресурсов.
Одним из ключевых аспектов оптимизации сети является управление трафиком. Это включает в себя стратегическое управление сетевым трафиком для достижения оптимальной производительности и распределения ресурсов. Такие методы, как формирование трафика, приоритизация и балансировка нагрузки, используются для обеспечения плавного потока данных, предотвращения узких мест и оптимизации использования полосы пропускания.
Оптимизация маршрутизации — еще одна важная область оптимизации сети. Он включает в себя поиск наиболее эффективных путей для передачи данных в сети. Алгоритмы оптимизации, такие как алгоритмы кратчайшего пути или протоколы маршрутизации, такие как OSPF или BGP, используются для определения наилучших маршрутов на основе таких факторов, как доступная пропускная способность, задержка канала и перегрузка сети. Оптимизируя маршрутизацию, сети могут свести к минимуму задержки, уменьшить потерю пакетов и повысить общую производительность.

Оптимизация качества обслуживания (QoS) является ключевым аспектом оптимизации сети. Он включает в себя определение приоритетов и распределение сетевых ресурсов на основе конкретных требований различных приложений или служб. Оптимизация QoS гарантирует, что критически важные приложения получат необходимую полосу пропускания и сетевые ресурсы, что повышает их производительность и удобство работы пользователей.
Оптимизация сетевых протоколов направлена на оптимизацию протоколов, используемых в сетевой связи. Такие методы, как оптимизация TCP, при которой протокол TCP точно настраивается для снижения накладных расходов и повышения эффективности, могут значительно повысить производительность сети. Кроме того, можно использовать методы сжатия протокола, чтобы свести к минимуму размер пакетов данных, передаваемых по сети, уменьшить задержку и повысить общую пропускную способность.
Оптимизация проектирования сети играет жизненно важную роль в обеспечении эффективной работы сети. Он включает в себя проектирование сетевых архитектур и топологий, которые минимизируют расстояние между узлами, уменьшают задержку и улучшают общую связность. Тщательно планируя структуру сети, организации могут оптимизировать поток данных, свести к минимуму узкие места и обеспечить эффективную связь между сетевыми устройствами.
Таким образом, сетевая оптимизация — это многогранный подход к повышению эффективности и производительности компьютерных сетей. С помощью управления трафиком, оптимизации маршрутизации, оптимизации QoS, оптимизации сетевых протоколов и оптимизации проектирования сети организации могут оптимизировать поток данных, сократить задержки, улучшить использование ресурсов и повысить общую производительность сети. Используя эти методы, предприятия могут повысить производительность, снизить затраты и обеспечить удобство работы пользователей в своих сетях.
Заключение
В заключение отметим, что двоичное дерево представляет собой структуру данных первостепенной важности в области компьютерных наук, предлагающую множество практических приложений. В этом исследовании мы обнаружили множество сценариев, в которых они могут быть плодотворно применены, тем самым подтвердив их незаменимость. Я надеюсь, что, освещая различные типы и области применения бинарных деревьев, я пролил свет на глубину и сложность, присущие этим мощным структурам.
Их масштабируемость, эффективность и способность упростить сложные вычислительные задачи делают бинарные деревья незаменимыми инструментами для любого ученого-компьютерщика. Хотя на первый взгляд они могут показаться пугающими, при твердом понимании и постоянной практике их потенциал можно использовать для решения даже самых сложных проблем.
Мир Binary Trees огромен, увлекателен и постоянно развивается. По мере того, как мы продолжаем разрабатывать более совершенные алгоритмы и структуры данных, мы можем ожидать, что применение и полезность двоичных деревьев будут становиться все более разнообразными. Имея эту основу понимания, интересно представить будущие инновации, которые содержит эта область.
Целью этой статьи было демистифицировать бинарные деревья, и я надеюсь, что это исследование пробудило ваше любопытство и побудило вас глубже погрузиться в мир структур данных и алгоритмов. Благодаря знаниям и пониманию мы можем раскрыть весь потенциал этих структур, формируя наш цифровой мир все более сложным и динамичным образом.