Как выполнить суммирование Эйнштейна в Python

В Python концепция суммирования Эйнштейна помогает нам упростить вычисления массивов. Она оказывает большую помощь при решении матриц, особенно при вычислении их векторного произведения, скалярного произведения, суммы диагоналей и т.д. В этой статье давайте рассмотрим эту концепцию и поймем функцию numpy.einsum().
Понимание суммирования Эйнштейна
Суммирование Эйнштейна — это то, что помогает нам работать с массивами и тензорами. Это помогает нам упростить такие выражения, как матрицы, тензоры и суммирование векторов.
Есть три жизненно важных правила, касающихся этой конвекции, которые следует учитывать:
- Когда индекс повторяется, он суммируется автоматически, без необходимости записи символа суммирования.
- Каждый индекс может повторяться только дважды в любом термине.
- Каждый термин должен иметь одинаковые неповторяющиеся индексы.
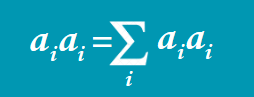
Я вижу, вы немного озадачены, читая теорию. Я согласен, что от Эйнштейна у нас постоянно болит голова, но не волнуйтесь: вы увидите, как это уравнение работает как волшебство в наших задачах с кодом. Давайте обсудим функцию Numpy, а затем перейдем к нескольким интересным примерам.
Функция numpy.einsum()
Функция numpy.einsum() выполняет суммирование Эйнштейна по предоставленным входным данным. Эта функция упрощает умножение матриц многомерных массивов. Давайте обсудим это подробно.
Синтаксис:
numpy.einsum(subscripts, *operands)Параметры:
Вот что означает каждый параметр в данном синтаксисе:
- subscripts: это строка, которая используется для указания операции.
- operands: это набор массивов, с которыми вы хотите работать.
Возвращаемое значение:
Этот метод возвращает соглашение Эйнштейна о суммировании для массивов операндов в соответствии с предоставленными индексами.
Работа numpy.einsum()
Давайте разберемся с работой функции numpy.einsum() на примере. Предположим, что есть два массива A и B и нам нужно их перемножить.
import numpy as np
A = np.array([[4, 2], [2, 4]])
B = np.array([[3, 6], [6, 3]])
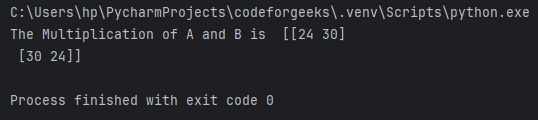
result = np.einsum('ij,jk->ik', A, B)
print("The Multiplication of A and B is ",result)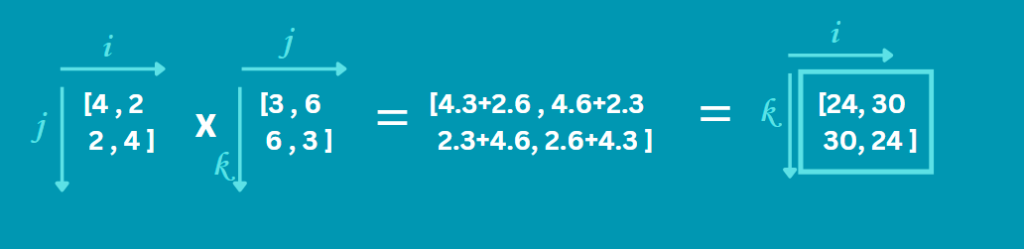
В строке ij,jk->ik ij представляет оси массива A, где i — для строк, а j — для столбцов. jk представляют собой оси массива B, где j — для строк, а k — для столбцов. Мы видим, что j повторяется, а это значит, что строки A умножаются на столбцы B, а поскольку j не включается в выходные данные, это означает, что полученное произведение суммируется. И вывод будет в виде 2D-массива, т.е. ik. Вот как мы получаем матричное умножение двух массивов, и результат ясно это подтверждает:
Практические примеры использования numpy.einsum()
Теперь, когда мы знаем, что einsum помогает нам с легкостью находить умножение матриц, это не единственное, в чем нам помогает einsum, его можно использовать по-разному. Все, что включает в себя комбинации осей умножения и суммирования, можно записать с помощью einsum. Давайте посмотрим, как это сделать.
Пример 1:
Мы можем узнать поэлементное умножение двух входных данных массива. Вот как нам в этом помогает einsum.
import numpy as np
A = np.array([4, 4, 4])
B = np.array([2 ,2 ,2])
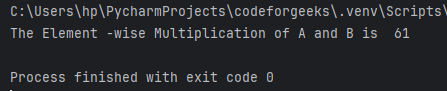
result = np.einsum('i,i->i', A, B)
print("The Element -wise Multiplication of A and B is ", result)В данном случае i,i->i означает, что мы берем элементы индекса i (строки) из массива A. Аналогичным образом мы берем элементы из массива B таким же образом, поскольку он также помечен как i. Затем мы умножаем соответствующие элементы вместе, чтобы получить результат.

Пример 2:
Если нам нужно вычислить скалярное произведение, мы можем использовать einsum следующим образом:
import numpy as np
A = np.array([4, 3, 2])
B = np.array([6 ,7 ,8])
result = np.einsum('i,i->', A, B)
print("The Dot product of A and B is ", result)Здесь i,i-> означает, что как из массива A, так и из массива B мы берем элементы строки, помеченные как i, и умножаем соответствующие элементы вместе. Но вместо того, чтобы сохранять каждый отдельный результат, просто суммируйте их. Таким образом, мы получаем скалярное произведение.
Пример 3:
Einsum также можно использовать для нахождения суммы главной диагонали. Вот код, в котором мы находим сумму диагональных элементов, используя einsum:
import numpy as np
A = np.array([[4, 1, 1],
[2, 4, 2],
[5, 5, 4]])
result = np.einsum('ii', A)
print("The sum of diagonal elements of A is ", result)В этом коде ii означает, что мы выбираем и суммируем только те элементы, которые имеют одинаковые индексы как для строк, так и для столбцов, что представляет собой не что иное, как диагональные элементы, следовательно, функция возвращает сумму всех диагональных элементов.

Заключение
Я надеюсь, что эта статья прояснит ваше представление о суммировании Эйнштейна в Python. Функция numpy.einsum() упрощает вычисления с массивами и тензорами, упрощая выполнение таких операций, как умножение матриц, скалярное произведение и диагональные суммы. Имея практические примеры, теперь вы можете использовать эту функцию для ускорения численных вычислений.