Линейная алгебра: LU-разложение с Python

В этой статье будет представлен способ решения линейной системы с использованием LU-декомпозиции.
LU Разложение
Декомпозиция Нижний-верхний (LU) - это способ разложить матрицу на множители как произведение нижней треугольной матрицы и верхней треугольной матрицы. Это можно рассматривать как матричную форму исключения Гаусса и является лучшим способом реализации исключения Гаусса, особенно для задачи с повторяющимся числом уравнений с одной и той же левой частью, т.е. для решения уравнения Ax = b с тем же A и разными значениями b.
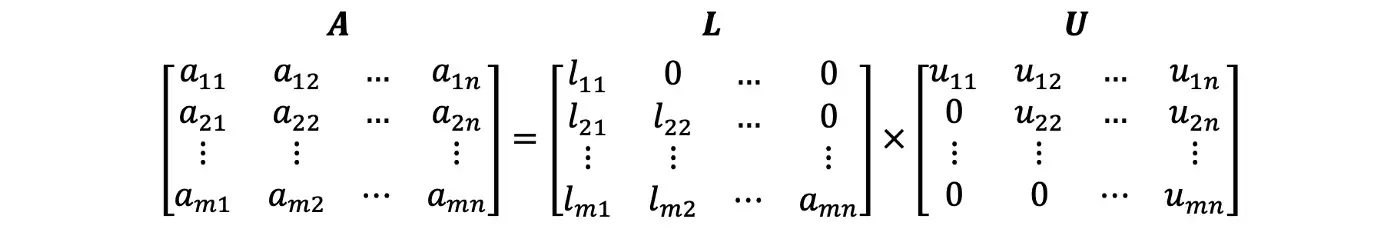
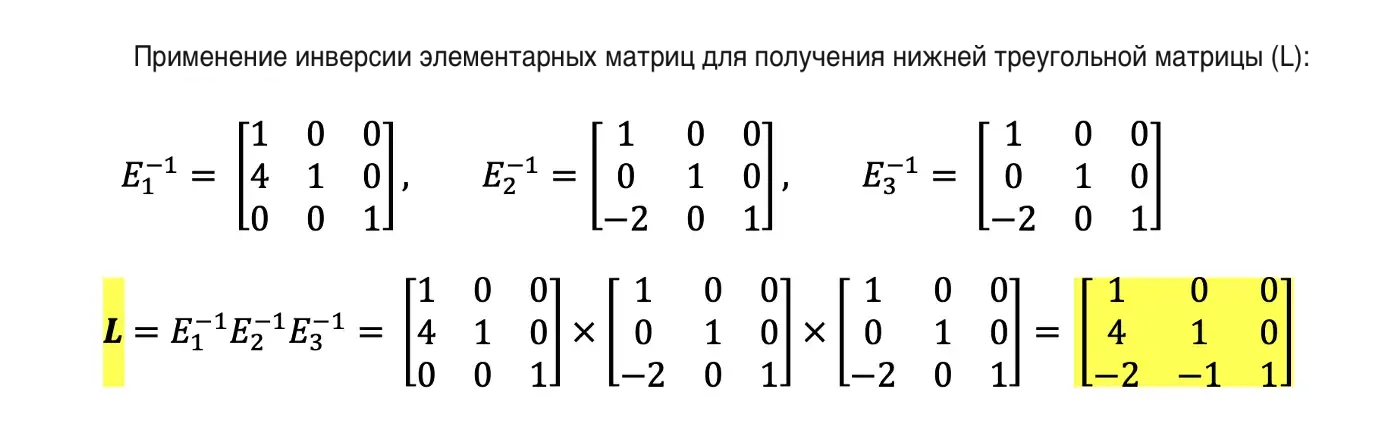
Матрица А может быть разложена на произведение нижней и верхней треугольных матриц с использованием элементарных матриц. Вы можете обратиться к предыдущей статье о трех различных элементарных матрицах: замена, масштабирование и поворотная матрица.

Теперь давайте рассмотрим, как решить линейную систему с помощью LU-декомпозиции.
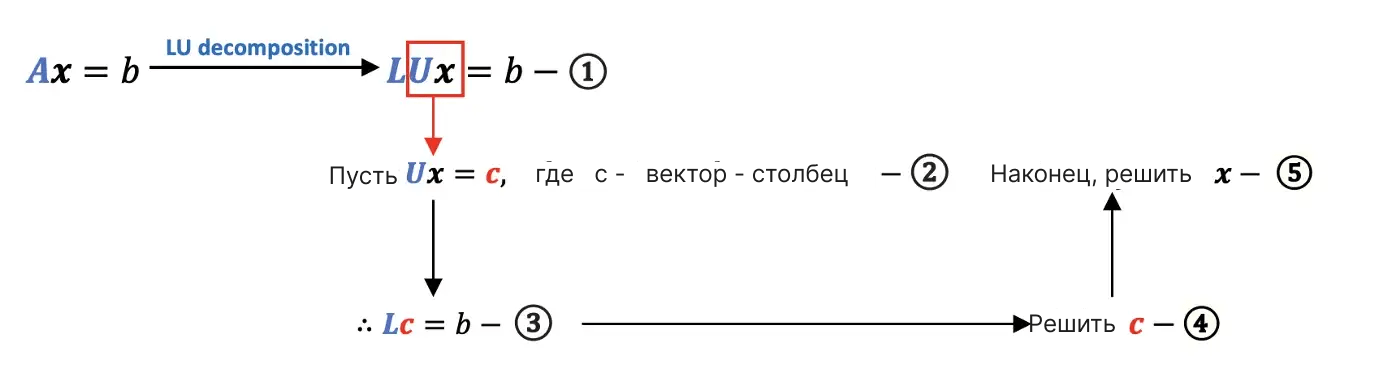
Пример использования LU-декомпозиции для решения линейной системы:
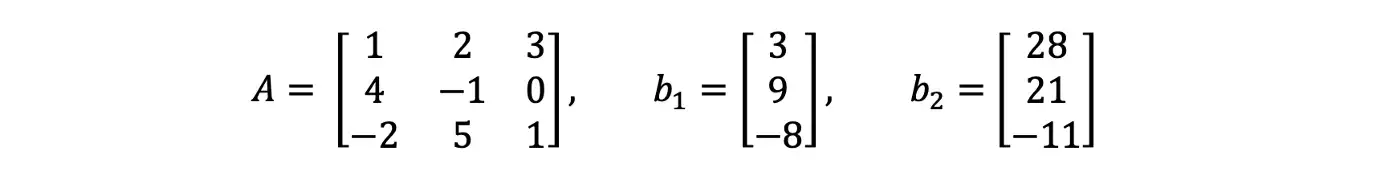
Шаг 1, 2, 3: Разложите матрицу A на матрицы L и U

Шаг 4: Используя Lc₁ = b₁ и Lc₂ = b₂, решите c₁ и c₂!
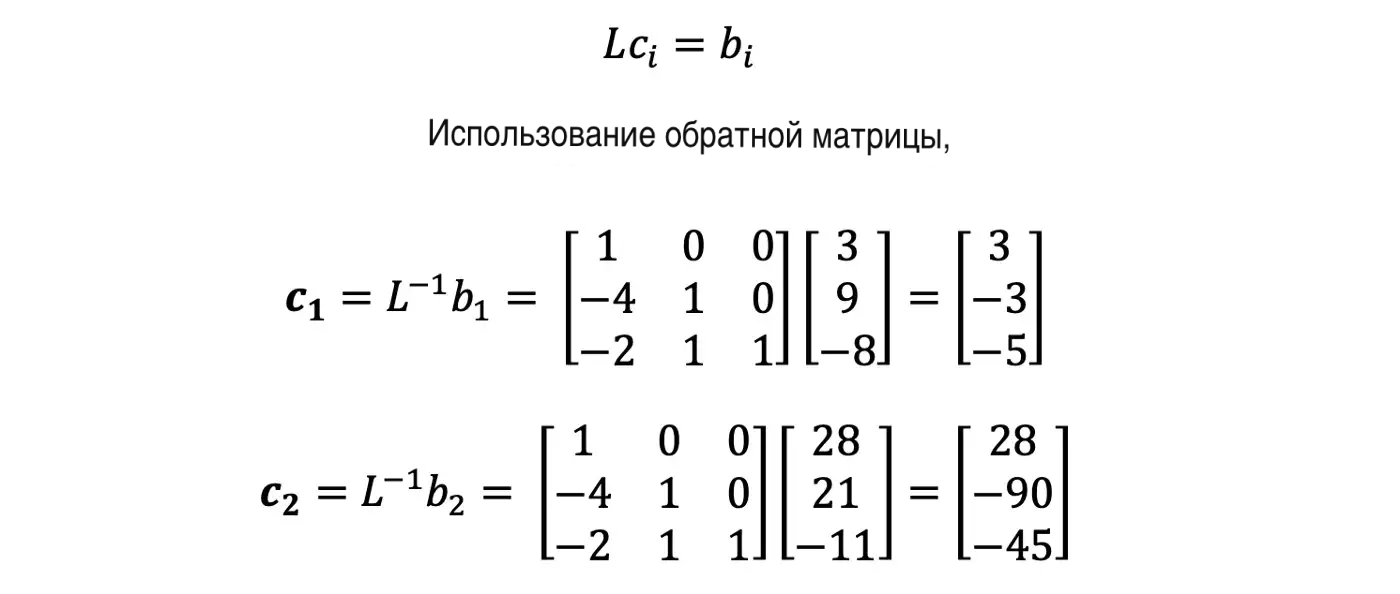
Шаг 5: Используя Ux₁ = c₁ и Ux₂ = c₂, решите x₁ и x₂!

Получив матрицы L и U, мы можем легко решить линейную систему с повторяющейся левой частью, как упоминалось выше.
import numpy as np
A = np.array([[1, 2, 3],
[4, -1, 0],
[-2, 5, 1]])
E1 = np.array([[1, 0, 0],
[-4, 1, 0],
[0, 0, 1]])
E2 = np.array([[1, 0, 0],
[0, 1, 0],
[2, 0, 1]])
E3 = np.array([[1, 0, 0],
[0, 1, 0],
[0, 1, 1]])
E1_inverse = np.linalg.inv(E1)
E2_inverse = np.linalg.inv(E2)
E3_inverse = np.linalg.inv(E3)
U = E3.dot(E2).dot(E1).dot(A)
L = E1_inverse.dot(E2_inverse).dot(E3_inverse)
print("\nStep 1 & 2: Upper traingular matrix of A using elementary matrices:")
print(U)
print("\nStep 1 & 3: Lower traingular matrix of A using inverse elementary matrices:")
print(L)
U_inverse = np.linalg.inv(U)
L_inverse = np.linalg.inv(L)
b1 = np.array([[3],
[9],
[-8]]) # column vector
c1 = L_inverse.dot(b1)
x1 = U_inverse.dot(c1)
print("\nStep 4a: Solve c1 given same left hand side matrix A but different right hand side b1:")
print(c1)
print("\nStep 5b: Solution x1 given same left hand side matrix A but different right hand side b1:")
print(x1)
b2 = np.array([[28],
[22],
[-11]]) # column vector
c2 = L_inverse.dot(b2)
x2 = U_inverse.dot(c2)
print("\nStep 4a: Solve c2 given same left hand side matrix A but different right hand side b2:")
print(c2)
print("\nStep 5b: Solution x2 given same left hand side matrix A but different right hand side b2:")
print(x2)
Резюме
Разложение LU используется для решения линейных систем и нахождения обратных матриц. Говорят, что это лучший метод решения линейной системы с повторяющейся левой частью. В этом посте вы узнаете, как решить линейную систему, используя разложение LU вместе с некоторыми кодами.