Полное руководство для начинающих по нотации Big O

Поскольку в программировании могут быть тысячи способов решения проблемы, как вы скажете, какой из них «лучший», или скажем, что есть функция, которая внедряется двумя разными способами, один с циклами, другой с помощью рекурсии, какой из этих способов должно быть использование в функции? Вот тут-то и появляется Big O — система, позволяющая выяснить, какой алгоритм требует больше времени для запуска и понимания. Алгоритм, который занимает меньше времени и менее сложен для понимания, выиграет.

Big O использует числа, чтобы сказать, какой алгоритм превосходен, а какой нужно переделать.

Зачем использовать Big O?

Причина даже использования Big O заключается не только в собеседованиях, но и при наличии больших наборов данных, поскольку в этот момент важна производительность. Поскольку данных много, алгоритмы, которым требуется час для сортировки или поиска в большом наборе данных, не так продуктивны, как алгоритм, которому для выполнения той же задачи требуются секунды.

Big O дает точный словарь, чтобы говорить о том, как работает наш алгоритм. Более того, это может помочь в обсуждении компромиссов между различными подходами и провести плодотворную дискуссию между разработчиками и инженерами о том, какой алгоритм будет работать лучше.

Big O также может помочь определить, какие части алгоритма неэффективны, и может помочь нам найти болевые точки в наших приложениях.

Что значит «лучше» или «лучший»?

Скажем, у нас есть функция, которая суммирует 'n':

function addUpTo(n) {
  let total = 0
  for (let index = 1; index <= n; index++) {
    total += index
  }
  return total
}

или же

function addUpTo(n) {
  return (n * (n + 1)) / 2
}

Какой из них будет считаться лучше, потому что один из них:

• Быстрее?
• Меньше памяти?
• Читабельнее?

Все это обоснованные опасения, как мы узнаем, какие из них лучше в целом?

В идеальном алгоритме должны быть учтены все три проблемы; однако в большинстве случаев скорость считается лучше, чем алгоритм с меньшим объемом памяти. К сожалению, удобочитаемость обычно упускается из виду чаще всего.

Сложность времени

Итак, давайте рассмотрим наиболее значительную скорость уступки или обычно называемую временной сложностью — это то, как мы анализируем время выполнения алгоритма по мере увеличения размера входных данных.

Сроки операции

Одним из способов проверки скорости является использование функций таймера, которые измеряют, как долго выполнялась служба. Измеряя производительность перед запуском функции, затем измеряя возврат после, затем вычитая разницу, чтобы показать, насколько быстро функция завершилась.

Как показано ниже для нашего addUpTo примера:

function addUpTo(n) {
  let total = 0
  for (let index = 1; index <= n; index++) {
    total += index
  }
  return total
}

let t1 = performance.now()

console.log(addUpTo(1000000))

let t2 = performance.now()

// Will be slower then the single line version of `addUpTo`
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)

или же

function addUpTo(n) {
  return (n * (n + 1)) / 2
}

let t1 = performance.now()

console.log(addUpTo(1000000))

let t2 = performance.now()

// Will be faster then the for loop version of `addUpTo`

console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)

Вручную замерять время не так практично. В долгосрочной перспективе, поскольку есть накладные расходы на его настройку, то как бы вы сообщали результаты в процентах или секундах.

Кроме того, есть проблема со временем в целом. Поскольку разные машины могут записывать разное время, поскольку каждая машина может быть настроена по-разному, поэтому результаты могут быть совершенно разными. Даже одно и то же устройство может иметь разные результаты. Для быстрых алгоритмов измерения скорости могут быть недостаточно точными.

Простые операции

Другим способом, помимо подсчета времени, является подсчет количества простых операций, которые компьютер должен выполнить, чтобы устранить проблему различных настроек компьютера, поскольку простые операции совпадают в функции. Итак, что считать простыми операциями. Это могут быть математические операции, такие как знаки плюс (+), минус (-), умножение (*) или деление (/). Вот ссылка на все простые операции. Однако было бы лучше, если бы вы не считали каждую операцию, а думали, где в функции происходит наибольшее влияние на память.

function addUpTo(n) {
  // Here there is only 3 operations (*, + and /)
  return (n * (n + 1)) / 2
}

function addUpTo(n) {
  let total = 0
  for (let index = 1; index <= n; index++) {
    // Here + is n additions since n is controlling the number of times the loop is going around i.e. n = 20 then it is 20 
operations Furthermore, = is a assignment operation so it can be count as well so with the example above the number of operations is 40
    total += index
  }
  return total
}

Подсчет простых операций может быть сложным, поэтому похоже, что количество простых операций будет больше в одной функциональной версии по сравнению с другой функциональной версией. Можно с уверенностью сказать, что тот, у которого наименьшее количество операций, может быть быстрее.

Правильное введение в Big O

Вот еще раз обзор, Big O Notation — это способ формализовать нечеткий счет, он позволяет нам формально говорить о том, как время выполнения алгоритма растет по мере роста входных данных. Кроме того, мы не заботимся о деталях, а только о том, каковы тенденции по мере роста входных данных. Большой O — это всегда максимум, с которым может справиться функция, прежде чем она начнет ломаться.

Определение

• f(n) = означает функцию с входом n

Мы говорим, что алгоритм равен O(f(n)), если количество простых операций, которые должен выполнить компьютер, в конечном счете меньше постоянного времени f(n) при увеличении n.

• f(n) может быть линейным (f(n) = n). Это означает, что время выполнения также масштабируется с таким представлением с n
• f(n) может быть квадратичным (f(n) = n²). Это означает, что время выполнения может быть возведено в квадрат, поэтому представляет собой n²
• f(n) может быть постоянным (f(n) = 1). Это означает, что время выполнения не влияет на время выполнения, поэтому оно совпадает по времени, поэтому представляет собой 1
• f(n) может быть чем-то совершенно другим.

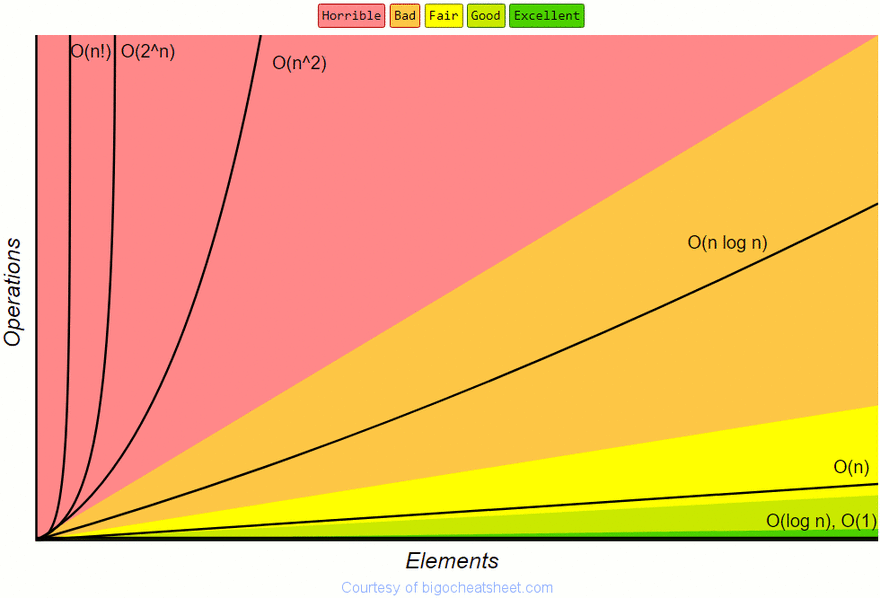
Вот график, показывающий рост операций и их влияние на алгоритм:

Пример того, что пытается сказать определение:

// Always 3 operations or O(1) since the number of operations does not grow
function addUpTo(n) {
  return (n * (n + 1)) / 2
}
// Number of operations is (eventually) bounded by a multple of n (say, 10n) or O(n) since the operations is bound by n
function addUpTo(n) {
  let total = 0
  for (let index = 1; index <= n; index++) {
    total += index
  }
  return total
}
function printAllPairs(n) {
  // The Big O For this function is O(n²) since the operations is bound by n twice
  for (let index = 1; index <= n; index++) {
    for (let innerIndex = 1; innerIndex <= n; innerIndex++) {
      console.log(index, innerIndex)
    }
  }
}

Упрощение выражений Big O

При определении временной сложности алгоритма существует критическое эмпирическое правило для значимых выражений O. Эти правила являются следствием определения нотации Big O. Таким образом, константы не имеют значения, поэтому O(2 n), т. е. 2 цикла For, имеют два O(n), поэтому функция равна O(n), поскольку функция будет медленной, несмотря ни на что. То же самое касается O(500), поскольку 500 означает количество операций в функции, поскольку количество операций не имеет значения, если операций не n, поэтому мы используем O(1), чтобы показать, что время выполнения совпадает.

Другой пример: O(13n²) может быть O(n²), поскольку 13 операций не имеют значения. O(n²) — самая слабая часть функции.

Чтобы еще больше упростить этот вопрос, вы должны посмотреть на тренды и увидеть, какое выражение является самым слабым из всех. Вы также можете использовать математику при сравнении выражений. Другой пример: O(n² + 5n + 8) будет равно O(n²), так как если n равно 10, то n² будет равно 100, 5*n будет равно 50, а 8 будет равно 8. Таким образом, поскольку n² имеет больше операций, чем два других, это самая слабая часть функции.

Эмпирические правила

1. Анализ сложности с помощью Big O может оказаться сложным, но есть эмпирические правила, которые могут помочь; однако эти правила не ВСЕГДА будут работать. Тем не менее, они являются важной отправной точкой.
2. Арифметические операции постоянны, так как большинство компьютеров могут выполнять эти операции примерно за время, необходимое для выполнения 2 + 2 операций на большинстве компьютеров.
3. Присвоение переменной также является постоянным, поэтому присваивание значения переменной в памяти должно происходить примерно в одно и то же время для всех машин.
4. Доступ к элементам в массиве (по индексу) или объекту (по ключу) является постоянным.
5. В цикле сложность равна длине цикла, умноженной на сложность всего, что происходит внутри цикла; это зависит от того, что такое петля. Если происходит больше циклов или других операций, это может увеличить время завершения цикла.

Вспомогательная космическая сложность (менее интенсивное использование памяти)

Сколько дополнительной памяти нам нужно выделить, чтобы запустить код в нашем алгоритме? Это вопрос, на который пытается ответить космическая сложность. Чем меньше памяти занимает алгоритм, тем меньше ваша программа используется для его запуска на компьютере пользователя. Таким образом, вы экономите деньги своих клиентов, поскольку вам не нужно обновлять их компьютеры для запуска вашего приложения.

Однако первая пространственная сложность — это и пространство, занимаемое входными данными, и переменные внутри алгоритма. Тем не менее, мы рассмотрим алгоритмы, которые не включают пространство, занимаемое входными данными, называемое сложностью вспомогательного пространства. Мы собираемся сосредоточиться на том, что происходит внутри алгоритма, а не на занимаемом пространстве ввода. Тем не менее, с этого момента я буду называть это космической сложностью.

Эмпирические правила

1. Эти правила предназначены для использования космической сложности.
2. Большинство примитивов (булевы значения, числа, нуль) представляют собой постоянное пространство, поскольку они требуют для обновления одного и того же объема пространства.
3. Для строк требуется O(n) пробела (где n — длина строки), поскольку строки составляют массив символов, поэтому количество символов в строке равно n.
4. Ссылочные типы обычно имеют значение O(n), где n — длина (для массивов) или количество ключей (для объектов), поскольку они состоят из примитивов, а диапазон равен n.

Например:

function sum(array) {
  let total = 0
  // For Space Complexity the Big O is O(1) since there is only two places where memory is being alloweded and is not in a loop so no n
  for (let index = 0; index < array.length; index++) {
    total = array[index]
  }
  return total
}

function double(array) {
  let newArr = []
  // For Space Complexity the Big O is O(n) since there is newArr is adding n elments in memoary so the amount of memoary can run out at Infintiy
  for (let index = 0; index < array.length; index++) {
    newArr.push(2 * array[index])
  }
  return newArr
}

Логарифмический

Ну, они не так распространены, как другие нотации Big O, O(1), O(n), O(n²), иногда они представляют собой выражения Big O, включающие более сложные математические выражения, которые являются выражением O(log n)

Логи — это обратные выражения, например, log²(8) = 3 → 2³ = 8 или log²(значение) = экспонента → 2^экспонента = значение, поэтому вы можете перемещать экспоненту и получать те же результаты, что и при умножении и делении. Журналы требуют базы, чтобы использовать их для получения дополнительной информации о логарифмическом просмотре по этой ссылке.

Поэтому, когда вы видите журнал в нотации Big O, это то же самое, что и log².

Чтобы упростить log², подумайте об этом, используя последовательное значение 2. Если n всегда равно двум, то это отличный кандидат на O(log n).

Клифф отмечает

Логарифм числа грубо измеряет, сколько раз вы можете разделить это число на два, прежде чем вы получите значение, меньшее или равное единице.

Например, 8/2 = 4/2 = 2/2 = 1 или log(8) = 3, так как 8 — это основание, а 3 — это количество логарифмических делений до достижения 0.

Какое значение имеет логарифмическая сложность

O(log n) является вторым лучшим выражением, которое следует за O(1), так как оно не так много, как O(1). В той же лопасти есть O(n log n), что является вторым худшим выражением для получения. Конкретные алгоритмы поиска имеют логарифмическую временную сложность, эффективные алгоритмы сортировки включают логарифмы, а рекурсия иногда требует логарифмического пространственного комплекса, поскольку они могут занимать n пространства.

Анализ производительности массива и объектов

Объект

Поскольку объекты являются типом структуры данных, поскольку они представляют собой ключ/значение, неупорядоченный список. Мы можем использовать нотацию Big O для объектов, чтобы делать, когда вы их используете.

Большой O объектов

Вот основы того, как объект работает, что вы можете сделать и как быстро это займет.

• Insertion: О(1)
• Removal: О(1)
• Searching: O(n)
• Access: O(1)

Поскольку объекты представляют собой бросок поиска в неупорядоченном списке, это означает, что JavaScript должен будет генерировать каждое значение до тех пор, пока не будет найдено такое же количество ключей. Для объектов, как правило, мы будем углубляться, когда доберемся до хеш-таблицы.

Большое О методов объектов

• Object.keys: O(n) — нужно бросить каждый ключ, чтобы получить ключ
• Object.values: O(n) — необходимо выбросить каждый ключ, чтобы получить его значение
• Object.entries: O(n) — необходимо выбросить каждый ключ, чтобы получить и ключ, и значение.
• hasOwnProperty: O(1) — Поскольку у hasOwnProperty есть аргумент, указывающий, какой ключ искать, и возвращать значение этого ключа.

Множество

Поскольку массивы являются типом структуры данных, поскольку они представляют собой ключ/значение, упорядоченный список. Мы можем использовать нотацию Big O для массивов, когда вы их используете.

Большое O массивов

Вот основы того, как работает массив, что вы можете сделать и как быстро это займет.

• Insertion: это зависит
• Removal: зависит
• Searching: O(n)
• Access: O(1) — поскольку массив связан с каждым элементом в памяти, JavaScript знает, в какой части памяти находится этот элемент, и получает данные из этой части памяти.

При вставке или удалении элементов для массива, если вы добавляете или удаляете элементы в конце массива, то это O(1) в любом другом месте это O(n), поскольку массив должен переиндексировать каждый элемент после нового элемента.

Большое О операций с массивами

• push: O(1) — добавляет в конец массива
• pop: O(1) - Удаляет конец массива
• shift: O(n) - Удаляет в начало массива
• unshift: O(n) — добавляет начало массива
• concat: O(n) — поскольку этот метод объединяет два или более массивов, размер этих массивов неизвестен n
• slice: O(n) — поскольку slice возвращает часть копии массива, поскольку неизвестно, насколько велика эта часть.
• splice: O(n) — поскольку splice добавляет или удаляет элементы из середины массива, поэтому неизвестно, сколько элементов будет затронуто этой функцией.
• sort: O(n*log n) - на данный момент это слишком сложно, посмотрите раздел сортировки
• forEach/map/filter/reduce/etc.: O(n): необходимо просмотреть каждый элемент массива.