Понимание нотации Big O через призму JavaScript

Если вы когда-нибудь задумывались о том, чтобы устроиться на работу в качестве разработчика, вы, вероятно, в какой-то момент натолкнулись на это интервью Google и задались вопросом: «О чем, черт возьми, они говорят?». В этой статье мы рассмотрим, что они имеют ввиду, разбрасывая такие термины, как «квадратичный» и «n log n».
В некоторых из этих примеров я буду ссылаться на эти два массива, один с 5 элементами и другой с 50. Я также собираюсь использовать удобный JavaScript Performance API для измерения разницы во времени выполнения.
const smArr = [5, 3, 2, 35, 2];
const bigArr = [5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2, 5, 3, 2, 35, 2];
Что такое Big O Notation?
Обозначение Big O - это просто способ представления общего роста вычислительной сложности задачи по мере увеличения набора данных. Несмотря на то, что существуют другие обозначения, обозначение O обычно используется наиболее часто, поскольку оно ориентировано на сценарий наихудшего случая, который легче оценить и обдумать. В худшем случае означает, что для выполнения задачи требуется больше всего операций; если вы решите кубик рубика за одну секунду, вы не сможете сказать, что вы лучший, если на это ушел всего один ход.
Когда вы узнаете больше об алгоритмах, вы увидите, что эти выражения часто используются, потому что написание кода при понимании этой взаимосвязи может быть разницей между почти мгновенной операцией или занятием минут и тратой, иногда огромных денег на внешние процессоры, такие как Firebase.
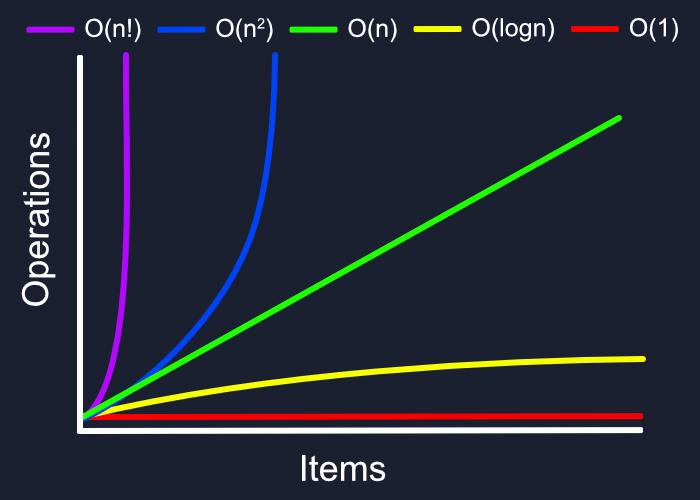
По мере того, как вы узнаете больше о нотации Big O, вы, вероятно, увидите много разных и лучших вариантов этого графа. Мы хотим сохранить нашу сложность как можно более низкой и прямой, в идеале избегая чего-либо выше O(n).
O(1)
Это идеальный вариант, независимо от того, сколько будет операций, будь то один или миллион, количество времени, которое нужно выполнить, останется неизменным. Большинство операций, которые выполняют одну операцию, являются O(1). Проход по массиву, получение элемента по определенному индексу, добавление дочернего элемента и т.д. Займет одинаковое количество времени независимо от длины массива.
const a1 = performance.now();
smArr.push(27);
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // Less than 1 Millisecond
const b1 = performance.now();
bigArr.push(27);
const b2 = performance.now();
console.log(`Time: ${b2 - b1}`); // Less than 1 Millisecond
O(n)
По умолчанию все циклы являются примером линейного роста, потому что существует взаимно-однозначное соотношение между размером данных и временем до завершения.
const a1 = performance.now();
smArr.forEach(item => console.log(item));
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // 3 Milliseconds
const b1 = performance.now();
bigArr.forEach(item => console.log(item));
const b2 = performance.now();
console.log(`Time: ${b2 - b1}`); // 13 Milliseconds
O(N^2)
Экспоненциальный рост - это ловушка, в которую мы все попали хотя бы раз. Нужно найти подходящую пару для каждого элемента в массиве? Помещение цикла в цикл - это отличный способ превратить массив из 1000 элементов при поиске в миллион операций, который заморозит ваш браузер. Всегда лучше выполнять 2000 операций над двумя отдельными циклами, чем миллион с двумя вложенными циклами.
const a1 = performance.now();
smArr.forEach(() => {
arr2.forEach(item => console.log(item));
});
const a2 = performance.now();
console.log(`Time: ${a2 - a1}`); // 8 Milliseconds
const b1 = performance.now();
bigArr.forEach(() => {
arr2.forEach(item => console.log(item));
});
const b2 = performance.now();
console.log(`Time: ${b2 - b1}`); // 307 Milliseconds
O(log n)
Лучшая аналогия, которую я слышал, чтобы понять логарифмический рост, это представить себе слово «нотация» в словаре. Вы не можете искать одну запись за другой, вместо этого вы найдете раздел «N», затем, возможно, страницу «OPQ», а затем выполните поиск по списку в алфавитном порядке, пока не найдете совпадение.
При таком подходе «разделяй и властвуй» количество времени, чтобы найти что-то, все равно будет меняться в зависимости от размера словаря, но ни в коем случае не близко к значению O(n). Поскольку поиск по более конкретным разделам происходит постепенно, не просматривая большую часть данных, поиск по тысяче элементов может занять менее 10 операций, в то время как миллион может занять менее 20, что принесет вам максимальную выгоду.
В этом примере мы можем сделать простую быструю сортировку.
const sort = arr => {
if (arr.length < 2) return arr;
let pivot = arr[0];
let left = [];
let right = [];
for (let i = 1, total = arr.length; i < total; i++) {
if (arr[i] < pivot) left.push(arr[i]);
else right.push(arr[i]);
};
return [
...sort(left),
pivot,
...sort(right)
];
};
sort(smArr); // 0 Milliseconds
sort(bigArr); // 1 Millisecond
O(n!)
Наконец, одна из худших возможностей - факториальный рост. Примером из учебника является проблема коммивояжера. Если у вас есть несколько городов разного расстояния, как найти кратчайший из возможных маршрутов, который проходит между ними и возвращается к начальной точке? Метод грубой силы должен был бы проверить расстояние между каждой возможной конфигурацией между каждым городом, которое было бы факториальным и быстро выходило из-под контроля.
Поскольку эта проблема очень быстро усложняется, мы продемонстрируем эту сложность с помощью короткой рекурсивной функции. Эта функция умножит число на собственную функцию, взяв в себя минус единицу. Каждая цифра в нашем факториале будет выполнять свою собственную функцию, пока не достигнет 0, при этом каждый рекурсивный слой добавляет свой продукт к нашему исходному номеру. Таким образом, 3 умножается на 2, что запускает умножаемую на 1 функцию, которая запускает ее снова и останавливается на 0, возвращая 6.
const factorial = n => {
let num = n;
if (n === 0) return 1
for (let i = 0; i < n; i++) {
num = n * factorial(n - 1);
};
return num;
};
factorial(1); // 2 Milliseconds
factorial(5); // 3 Milliseconds
factorial(10); // 85 Milliseconds
factorial(12); // 11,942 Milliseconds
Вместо этого я намеревался показывать factorial(15), но все, что выше 12, было слишком ресурсоемкое для выполнения, и это приводило к краху страницы, доказывая, почему именно этого следует избегать.
Заключительные мысли
Поддержание вашего кода как можно более быстрым может показаться очевидной проблемой, но я уверен, что почти каждый разработчик создал двойной или даже тройной вложенный цикл хотя бы один раз, потому что «он просто работает».