Построение глубокой нейронной сети с нуля с использованием Python
Эта статья посвящена созданию глубокой нейронной сети с нуля без использования таких библиотек, как Tensorflow, keras или Pytorch и т. д. Она состоит из двух разделов. В первой части мы увидим, что такое глубокая нейронная сеть, как она может учиться на данных, математику, стоящую за ней, а во второй части мы поговорим о ее создании с нуля с использованием Python.
Если вы знакомы с концепциями нейронной сети, не стесняйтесь пропустить первую часть и сразу перейти к разделу «Построение сети для идентификации рукописных цифр».
Что такое глубокая нейронная сеть?
Прежде чем мы фактически перейдем к искусственному нейрону и нейронной сети, давайте посмотрим, как функционирует наша биологическая нейронная сеть.
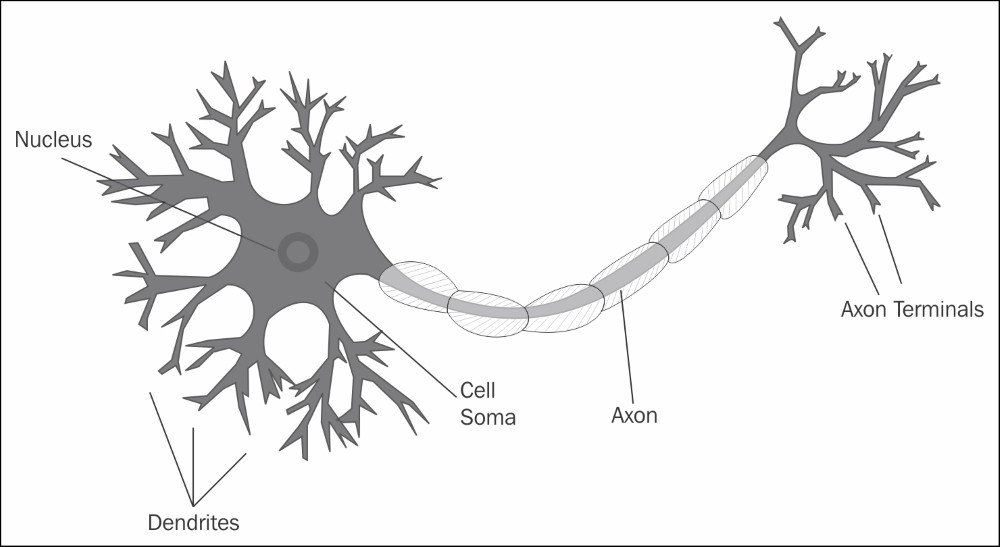
Биологическая нейронная сеть - это сеть взаимосвязанных нейронов. Каждый нейрон имеет так называемые дендриты, которые собирают информацию из окружающей среды. Информация поступает в нейрон в виде электрических / химических сигналов. Как только нейрон получает сигнал, он обрабатывает сигнал и, если он достигает определенного порога, излучает выходной сигнал через аксон, который подключен к следующему нейрону. Следующий нейрон после получения сигнала делает то же самое, и процесс продолжается.
Искусственная нейронная сеть (ANN) смутно вдохновлена биологической нейронной сетью. Это набор связанных искусственных нейронов. Как и биологический нейрон, искусственный нейрон также принимает входные данные от одного нейрона, выполняет некоторые вычисления и передает сигнал другому нейрону, который к нему подключен.
Глубокая нейронная сеть (DNN) - это искусственная нейронная сеть с несколькими уровнями между входным и выходным уровнями. Каждый нейрон в одном слое соединяется со всеми нейронами следующего слоя. Один или несколько слоев между входным и выходным слоями называются скрытыми слоями.
Каждое соединение, которое соединяет нейрон из одного слоя с нейроном в предыдущем слое, имеет так называемый вес w, который говорит о том, насколько чувствительна активация нашего текущего нейрона к активации нейрона в предыдущем слое. Каждый нейрон в данном слое имеет нечто, называемое смещением b. Если вы знакомы с линейной регрессией, член смещения действует как перехватчик «c» в y = mx + c. Если сумма (mx) не пересекает порог, но нейрон должен активироваться, смещение будет скорректировано, чтобы понизить порог этого нейрона, чтобы заставить его сработать.
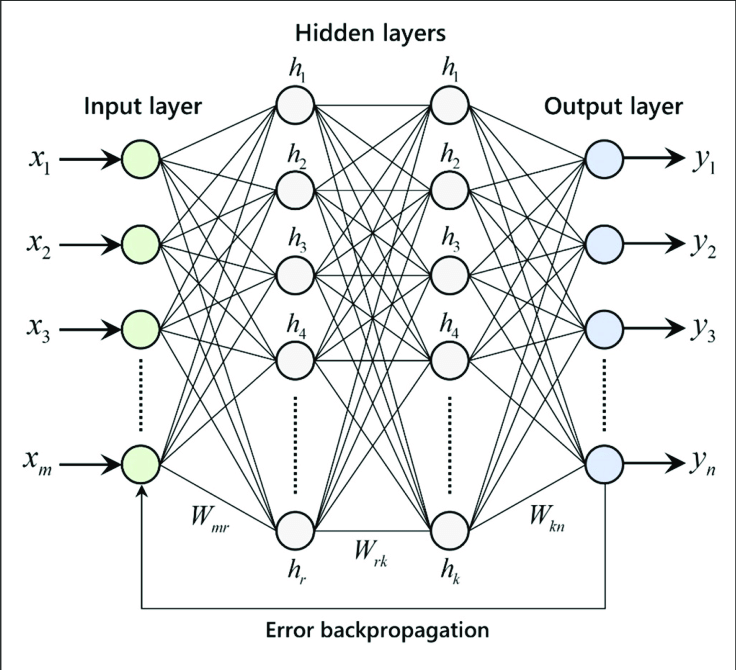
Вся сеть выглядит очень сложной, верно! Но это не так. Думайте об этом как о гигантской функции y = f (x), где x - ваш вход, y - выход. Затем внутри функции f (x) она вызывает цепочку функций, в которой вывод одной функции передается другой. Эти внутренние функции - не что иное, как скрытые слои.
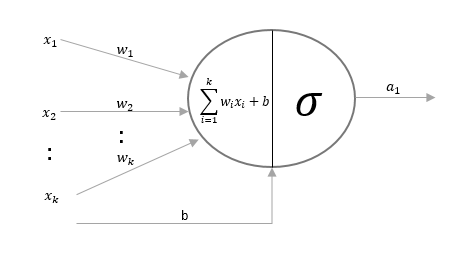
Теперь давайте увеличим масштаб до одного искусственного нейрона. Искусственный нейрон состоит из двух частей. В первой части он берет входные данные из предыдущего слоя, соответствующие веса, смещения, а затем выполняет линейное преобразование этих данных. Линейное преобразование - это не что иное, как сумма взвешенных входных данных и смещения.
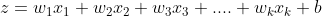
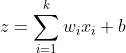
Во второй части он преобразует это линейное преобразование в нелинейное преобразование, используя функцию активации, такую как сигмоид, и испускает выходной сигнал функции активации. Есть и другие различные функции активации, такие как ReLu, но в этом посте мы используем сигмоид. Из-за этой комбинации линейных и нелинейных преобразований вместе с несколькими уровнями глубокая нейронная сеть становится настолько мощной, что она может обрабатывать любые сложные данные.
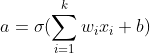
Сигмоидная функция принимает взвешенную сумму и преобразует значение от 0 до 1. Она преобразует -infinity в 0 и + infinity в 1. Значение между 0 и 1 представляет силу активации конкретного нейрона.
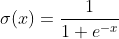
Активацию нейрона на данном слое можно записать следующим образом:
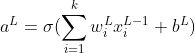
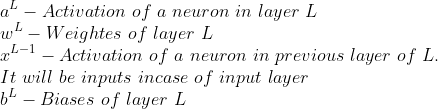
В типичной нейронной сети у нас будет более одного нейрона в данном слое. Вышеупомянутое уравнение может быть представлено в виде матрицы, включающей все нейроны.

Обучение глубокой нейронной сети
Глубокая нейронная сеть сама будет учиться на предоставленных данных и будет использоваться для прогнозирования невидимых данных. Но что мы подразумеваем под обучением на основе данных?
Как мы уже обсуждали, DNN имеет набор весов и смещений на каждом уровне. Активация нейрона зависит от соответствующих весов и смещений. Таким образом, обучение на основе данных означает определение наилучших весов и смещений сети. Но как нам найти веса и смещения?
Чтобы найти веса и смещения, глубокая нейронная сеть делает следующее:
- Присваивает весам и смещениям некоторые случайные значения
- Запускает обучающие данные (которые имеют входные и фактические выходы) в сети, используя эти случайно назначенные веса и смещения. Во время этого выходные данные функции активации в одном слое будут передаваться в качестве входных данных на следующий уровень, пока мы не получим выходные данные из выходного слоя. Этот процесс называется прямым распространением.
- Первоначальный вывод из сети всегда будет ужасным, поскольку мы использовали случайные веса и смещения. Мы вычисляем ошибку (разницу между предсказанием сети и фактическим выходом), используя какую-то функцию стоимости или ошибки. В этом посте мы собираемся использовать сумму квадратов ошибок.
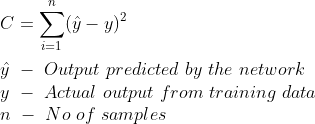
4. Поскольку все нейроны в сети внесли свой вклад в ошибку, указанную выше, пропорция ошибки (градиент ошибки) будет передана обратно из выходного слоя во все слои, за исключением входного, чтобы можно было регулировать веса и смещения. Этот процесс распространения ошибки для корректировки весов и смещений называется обратным распространением.
Поскольку функция стоимости является функцией весов и смещений, градиент ошибки будет вычисляться с использованием частных производных функции стоимости по весам и смещениям.
Чтобы лучше понять, давайте возьмем простую сеть с одним входным слоем, одним скрытым слоем и одним выходным слоем. После первого прохода прямого распространения у нас будет ошибка. Теперь нам нужно передать пропорцию ошибки всем нейронам во всех слоях.
Сначала давайте вычислим градиент ошибки для небольшого изменения весов и смещений на выходном слое. Для простоты запишем функцию активации как функцию функции.
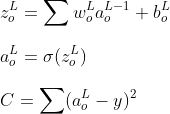
Пришло время обновить многомерное исчисление в средней школе / колледже и найти частные производные функции стоимости C как по весу, так и по смещению. Используя правило цепи, частную производную от C и b можно записать следующим образом.
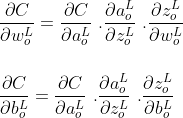
Частные производные каждого компонента в приведенном выше уравнении равны
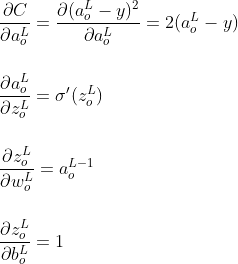
Подставляя указанные выше значения частных производных в уравнение правила цепи, градиенты ошибок на выходном слое относительно весов и смещений равны
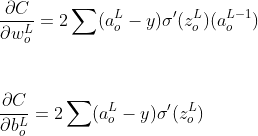
Теперь давайте посчитаем для скрытого слоя
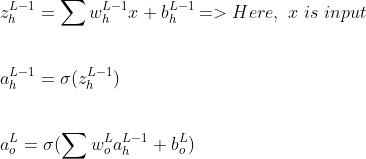
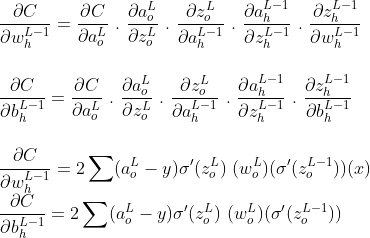
Примечание. Хотя L и L-1 представляют выходной слой и скрытый слой соответственно, я использовал суб-нотацию «o» для вывода и «h» для скрытого слоя, чтобы быть более четким.
Точно так же мы можем вычислить градиент ошибки на всех скрытых слоях, если у нас их больше одного. Поскольку у нас есть только один скрытый слой, обратное распространение здесь останавливается.
5. Вышеупомянутое прямое и обратное распространение будет выполняться итеративно, а веса и смещения будут корректироваться до тех пор, пока мы не найдем оптимальные значения. Вместо того, чтобы делать это как подход грубой силы, мы будем использовать алгоритм градиентного спуска.
Градиентный спуск
Градиентный спуск является итеративным методом оптимизации, который может найти минимум в виде функции. Он используется, когда поиск оптимальных значений параметров функции затруднен алгебраически.
Интуиция: представьте себе человека, стоящего на обрыве долины. Человек хочет добраться до дна долины, но не знает, в каком направлении он спустится. Он делает один шаг, выбирает следующую позицию на основе текущей позиции. Если он сделал шаг вниз, он продолжит движение в том же направлении, в противном случае он изменит свое направление. Он делает большие шаги, когда склон долины крутой, и, достигая дна долины, он делает шаги меньшего размера. Наконец останавливается, когда достигает дна долины.
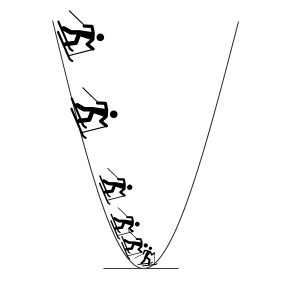
Наша цель здесь - найти оптимальные значения весов и смещений, при которых функция стоимости будет минимальной. Следующие шаги используются в алгоритме градиентного спуска.
- Назначьте случайные значения для весов w и смещений b и постоянное значение для скорости обучения
- Обновите веса и смещения, используя градиент (мы рассчитали с использованием частных производных) и скорость обучения.
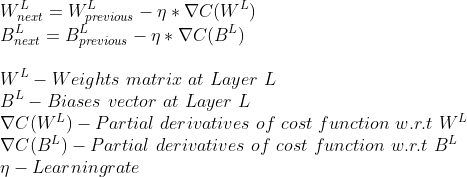
3. Повторяйте шаг 2, пока не найдем минимальное значение или не достигнем максимального количества итераций.
Резюме обучения
Подведем итог всему процессу обучения, написав псевдокод для сети, которая имеет 1-входной, 1-скрытый и 1-выходной уровни.
initialize_weights_and_biases():
output_w = initialize_random_w
output_b = initialize_random_b
hidden_w = initialize_random_w
hidden_b = initialize_random_b
train(x_train, y_train, no_of_iterations, learning_rate):
# 1. initialize network weights and biases
initialize_weights_and_biases()
for iteration in range(no_of_iterations): #Run gradient descent algorithm no_of_iterations times
#initialize delta of weights and biases
wo_delta = initialize_random_w_delta
bo_delta = initialize_random_b_delta
wh_delta = initialize_random_w_delta
wh_delta = initialize_random_b_delta
for x, y in zip (x_train, x_train): #Iterate through each sample in the training data
# 2.forward propagation
z_h = hidden_w * x + hidden_b
a_h = sigmoid(z_h )
z_o = output_w * a+ output_b
predicted = sigmoid(z_o)
# 3.find the error
error = (predicted - y)
# 4.Back propagate the error
delta = 2 error * sigmoid_prime(z_o)
wo_delta+= delta * a_h
bo_delta+= delta
wh_delta+= delta * output_w * sigmoid_prime(z_h) * x
bh_delta+= delta * output_w * sigmoid_prime(z_h)
# 5. after 1 pass of all the inputs, update the network weights
output_w = output_w - learning_rate * wo_delta
output_b = output_b - learning_rate * bo_delta
hidden_w = hidden_w - learning_rate * wh_delta
hidden_b = hidden_b - learning_rate * bh_deltaПрогноз
После обучения нейронной сети у нас будут оптимальные значения весов и смещений на каждом слое. Прогнозирование - это не что иное, как выполнение одного прохода прямого распространения для тестовых данных.
Создание сети для распознавания рукописных цифр
Хватит теории, давайте запачкаем руки, написав программу на Python для построения глубокой нейронной сети. Мы собираемся использовать набор данных mnist и построить сеть, распознающую рукописные цифры, программу hello world Deep Neural Network.
Данные mnist состоят из сканированных рукописных изображений размером 28 x 28 пикселей.

Мы снова рассмотрим создание сети с 1 входным слоем, 1 скрытым слоем и 1 выходным слоем.
Следующая программа представляет собой версию псевдокода для Python, о которой мы говорили выше. Единственная разница в том, что мы ввели пакетную обработку, потому что mnist data содержит 60000 строк данных. Загрузка всех 60000 строк в память для каждой итерации уничтожит память.
def sigmoid(z):
return 1.0/(1.0 + np.exp(-z))
def sigmoid_prime(z):
return sigmoid(z)*(1-sigmoid(z))
def vectorized_result(j):
e = np.zeros((10, 1))
e[j] = 1.0
return e
class NeuralNetwork:
def __init__(self, layers):
self.h_biases = np.random.randn(layers[1],1)
self.o_biases = np.random.randn(layers[2],1)
self.h_weights = np.random.randn(layers[1],layers[0])
self.o_weights = np.random.randn(layers[2],layers[1])
def forward_propagation(self, x):
a = sigmoid(np.dot(self.h_weights, x) + self.h_biases)
output = sigmoid(np.dot(self.o_weights, a) + self.o_biases)
return output
def update_mini_batch(self, batch, l_rate):
o_b = np.zeros(self.o_biases.shape)
h_b = np.zeros(self.h_biases.shape)
o_w = np.zeros(self.o_weights.shape)
h_w = np.zeros(self.h_weights.shape)
for x, y in batch:
o_del_b, h_del_b, o_del_w, h_del_w = self.backprop(x,y)
o_b = o_b + o_del_b
h_b = h_b + h_del_b
o_w = o_w + o_del_w
h_w = h_w + h_del_w
self.o_weights = self.o_weights - (l_rate/len(batch))*o_w
self.h_weights = self.h_weights - (l_rate/len(batch))*h_w
self.o_biases = self.o_biases - (l_rate/len(batch))*o_b
self.h_biases = self.h_biases - (l_rate/len(batch))*h_b
def backprop(self, x, y):
z_h = np.dot(self.h_weights, x) + self.h_biases
a_h = sigmoid(z_h)
z_o = np.dot(self.o_weights, a_h) + self.o_biases
predicted = sigmoid(z_o)
delta = (predicted - y) * sigmoid_prime(z_o)
o_del_b = delta
o_del_w = np.dot(delta, a_h.transpose())
delta = np.dot(self.o_weights.transpose(), delta) * sigmoid_prime(z_h)
h_del_b = delta
h_del_w = np.dot(delta, x.transpose())
return (o_del_b, h_del_b, o_del_w, h_del_w)
def fit(self, train_data, epochs, mini_batch_size, learning_rate):
n = len(train_data)
for i in range(epochs):
random.shuffle(train_data)
batches = [train_data[j:j+mini_batch_size] for j in range(0,n, mini_batch_size)]
for batch in batches:
self.update_mini_batch(batch, learning_rate)
print("epoch {} completed".format(i))
def accuracy(self, test_data):
test_results = [(np.argmax(self.forward_propagation(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)__init__ инициализирует веса и смещения случайным образом для выходных и скрытых слоев.
forward_propagation выполняет прямое распространение для данного ввода
update_mini_batch выполняет прямое и обратное распространение для каждой записи в данном пакете. Мы делаем сумму дельты ошибок, потому что мы используем сумму квадратов ошибок, а частная производная - это сумма градиента ошибок всех выборок.
o_del_b, h_del_b, o_del_w, h_del_w = self.backprop(x,y)
o_b = o_b + o_del_b
h_b = h_b + h_del_b
o_w = o_w + o_del_w
h_w = h_w + h_del_wПосле каждого пакетного запуска он будет обновлять веса и смещения сети.
self.o_weights = self.o_weights — (l_rate/len(batch))*o_w
self.h_weights = self.h_weights — (l_rate/len(batch))*h_w
self.o_biases = self.o_biases — (l_rate/len(batch))*o_b
self.h_biases = self.h_biases — (l_rate/len(batch))*h_bbackprop распространяет градиент ошибки обратно на все слои, кроме входного. Это сердце нейронной сети. Как мы обсуждали ранее, мы будем вычислять частные производные функции ошибок по весам и смещениям на каждом уровне. В коде мы использовали метод .transpose (), чтобы он соответствовал правилу умножения матриц ( AXB возможен, только если A является матрицей mXn, а B - матрицей nXp. Матрица результата будет mXp).
delta = (predicted - y) * sigmoid_prime(z_o)
o_del_b = delta
o_del_w = np.dot(delta, a_h.transpose())
delta = np.dot(self.o_weights.transpose(), delta) * sigmoid_prime(z_h)
h_del_b = delta
h_del_w = np.dot(delta, x.transpose())Метод fit обучает сеть. Он принимает входные данные, перемешивает их в случайном порядке, разбивает данные на пакеты. Вызывает функцию update_mini_batch для каждого пакета.
Чтобы прочитать данные mnist, мы собираемся использовать fetch_openml из пакета sklearn.datasets. Мы будем использовать sklearn, чтобы разделить данные для обучения и тестирования.
X, y = fetch_openml('mnist_784', return_X_y=True)
y = y.astype(int)
X = (X/255).astype('float32')
X = [np.reshape(x, (784, 1)) for x in X]
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2, random_state=7)
y_train = [vectorized_result(i) for i in y_train]Данные mnist содержат оцифрованные изображения рукописных цифр, поэтому они будут иметь значения от 0 до 255. Чтобы нормализовать данные, разделите входные данные на 255, чтобы распределение изображений было между 0 и 1.
X = (X/255).astype('float32')Поскольку каждое изображение имеет размер 28 x 28 пикселей и глубокая нейронная сеть ожидает ввода в векторном формате, ввод преобразуется в форму (784,1), потому что 28 * 28 = 784.
X = [np.reshape(x, (784, 1)) for x in X]Сеть, которую мы собираемся построить, имеет 10 нейронов в выходном слое, поскольку нам нужно идентифицировать цифры от 0 до 9. Если сеть идентифицирует данную цифру как 3, то выходной нейрон, предназначенный для 3, будет иметь значение 1 а все остальные нейроны будут иметь значение 0.
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0]Поскольку набор данных mnist имеет значение y в виде цифры, нам нужно векторизовать его так, чтобы он был в форме, упомянутой выше.
def vectorized_result(j):
e = np.zeros((10, 1))
e[j] = 1.0
return e
y_train = [vectorized_result(i) for i in y_train]Давайте создадим сетевой объект, указав количество нейронов на каждом слое, и обучим сеть с помощью данных обучения.
network = NeuralNetwork([784, 100, 10])
train_data = list(zip(X_train, y_train))
network.fit(train_data, 30, 10, 3.0)Здесь у нас есть сеть с входным слоем из 784 нейронов, скрытым слоем из 100 нейронов (почему 100 нейронов? Это выбор, мы можем использовать любое количество нейронов и посмотреть, как ведет себя сеть) и выходной слой из 10 нейронов.
network.fit(train_data, 30, 10, 3.0)Приведенный выше оператор разбивает входные данные на 10 пакетов и выполняет 30 итераций со скоростью обучения 3. Число итераций, пакет и скорость обучения являются гиперпараметрами сети. Нам нужно выполнить настройку гиперпараметров, чтобы найти лучшую комбинацию.
Точность
Чтобы определить точность модели по сравнению с тестовыми данными, для каждых данных, выполняющих прямое распространение, получите максимальное значение. Если значение соответствует критерию y, это правильный прогноз модели. Сумма правильных прогнозов по общему количеству тестовых данных дает точность

Для построенной нами сети точность тестирования составляет 96,59%, что очень хорошо.
Полная программа доступна в моем репозитории git