Предсказать, есть ли у пациента диабет, с помощью линейного дискриминантного анализа (LDA) за 6 шагов по шкале R
В этой статье мы будем использовать Линейный дискриминантный анализ (LDA) для решения задачи классификации. В то время как логистическая регрессия использует Логит-модель для определения условной вероятности (вероятности события A при условии, что событие B уже произошло), LDA использует теорему Байеса для определения условной вероятности (Условная вероятность - это вероятность события, которое произойдет, учитывая, что другое событие уже произошло раньше). LDA берет среднее значение каждой ковариаты при нормальном распределении в каждом классе K и находит вероятность по следующей формуле. (Мы не будем заострять на этом внимание, наша цель - увидеть его использование с R)

Мы также рассмотрим практические примеры LDA с языком R программирования. Мы будем использовать набор данных о диабете, чтобы предсказать, есть ли у пациента диабет или нет, на основе заданных переменных.
Набор данных диабета
Наш набор данных состоит из ковариат и переменной ответа. Переменная ответа, которая является результатом, показывает, болен ли пациент диабетом или нет. Мы будем использовать этот набор данных, чтобы разделить его на обучающие и тестовые подмножества для разработки нашей модели LDA и прогнозирования наличия у пациента диабета. В конце мы запустим матрицу неточностей, чтобы увидеть точность нашей модели. Пойдем шаг за шагом.
Шаг 1. Знайте свой набор данных
Знакомство с набором данных очень важно, если вы не хотите впоследствии подвергаться критике из-за вводящего в заблуждение анализа.
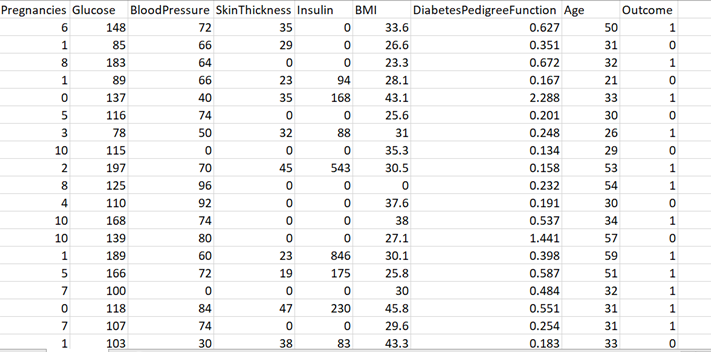
Шаг 2. Поэкспериментируйте с набором данных
Преобразуйте числовое значение в факториал
data = data %>% mutate(Outcome = factor(Outcome, levels=c(0,1),labels=c("no","yes")))
Давайте сделаем просто простой столбчатый график нашей переменной ответа
data %>% ggplot(aes(Outcome))+
geom_bar(fill='blue')
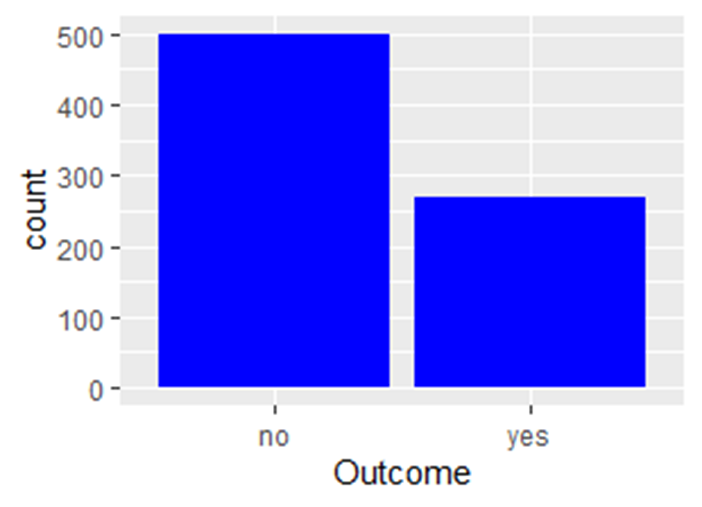
Шаг 3. Разделите набор данных на обучающие и тестовые подмножества.
# Прогнозирование: давайте сначала добавим идентификационный номер для пациентов
data = data %>% mutate(id = row_number())
# Затем разделите набор данных на обучающие и тестовые данные.
set.seed(11, sample.kind=”Rejection”)
tr_index = sample(1:nrow(data),0.7*nrow(data), replace=FALSE)
train=data[tr_index,]
test=data[-tr_index,]
Шаг 4: Создайте свою модель с библиотекой MASS
library(MASS)
LDA = lda(Outcome~.,data=train)
LDA
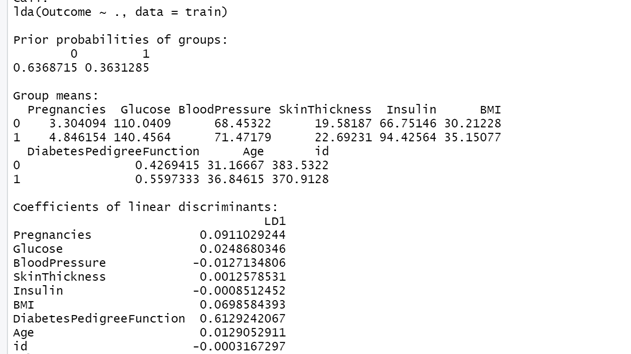
- Prior: R принимает гипотезу вероятности, прежде чем мы приступим к ее анализу.
- Group означает: Каково среднее значение для каждой переменной
- Coefficients of Linear Discriminants: это дискриминантная функция, которую мы находим для модели.
Шаг 5: прогноз
lda_pred = predict(LDA, newdata = test)
names(lda_pred)
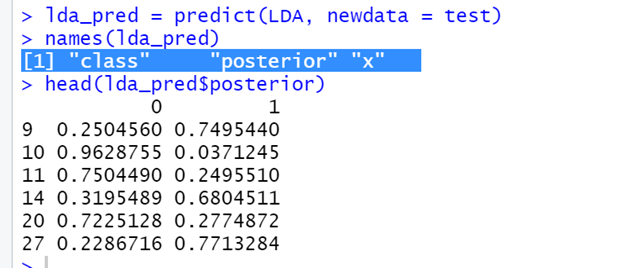
- Здесь у нас 3 имени.
- Posterior - это проблема после LDA
- Class - это классификация, которая будет полезна для прогноза
- Если вы посмотрите ниже, вероятность для каждого класса дана в соответствующей группе.
Шаг 6. Подтвердите свою модель с помощью матрицы неточностей.
perf_indexes = function(cm){
sensitivity = cm[2,2] / (cm[1,2] + cm[2,2])
specificity = cm[1,1] / (cm[1,1] + cm[2,1])
accuracy = sum(diag(cm)) / sum(cm)
return(c(sens=sensitivity,spec=specificity,acc=accuracy))
}
perf_indexes(table(lda_pred$class, test$Outcome))

Всякий раз, когда вы хотите понять, хорошо ли работает ваша модель, вы должны использовать матрицу неточностей. В матрице неточностей у вас есть:
- sensitivity - чувствительность (истинно положительный показатель): TP / P
- specificity - специфичность (истинно отрицательный показатель): TN / N
- accuracy - точность (процент правильно классифицированных наблюдений): (TN + TP) / (N + P)