Что такое кодирование Хаффмана?

Алгоритм кодирования Хаффмана является строительным блоком многих алгоритмов сжатия, таких как DEFLATE, который используется форматом изображений PNG и GZIP.
Почему это должно меня беспокоить?
Вы когда-нибудь хотели знать:
- Как что-то сжать без потери данных?
- Почему одни вещи сжимаются лучше, чем другие?
- Как работает GZIP?
Предположим, мы хотим сжать строку (кодирование Хаффмана можно использовать с любыми данными, но строки являются хорошими примерами).
Неизбежно, что некоторые символы будут появляться в тексте для сжатия чаще, чем другие. Кодирование Хаффмана использует этот факт и кодирует текст так, чтобы наиболее часто используемые символы занимали меньше места, чем менее распространенные.
Кодирование строки
Давайте воспользуемся кодировкой Хаффмана, чтобы сжать (частичную) цитату Йоды; «do or do not».

«do or do not» - это 12 символов. В ней есть несколько повторяющихся символов, поэтому он должен хорошо сжиматься.
В качестве аргумента мы предположим, что для хранения каждого символа требуется 8 бит (кодирование символов - это совсем другая тема). Это предложение обойдется нам в 96 бит, но мы можем добиться большего с помощью кодирования Хаффмана!
Начнем с построения древовидной структуры. Наиболее распространенные символы в наших данных будут ближе к корню дерева, в то время как узлы, наиболее удаленные от корня, представляют менее распространенные символы.
Вот дерево Хаффмана для строки «do or do not»:
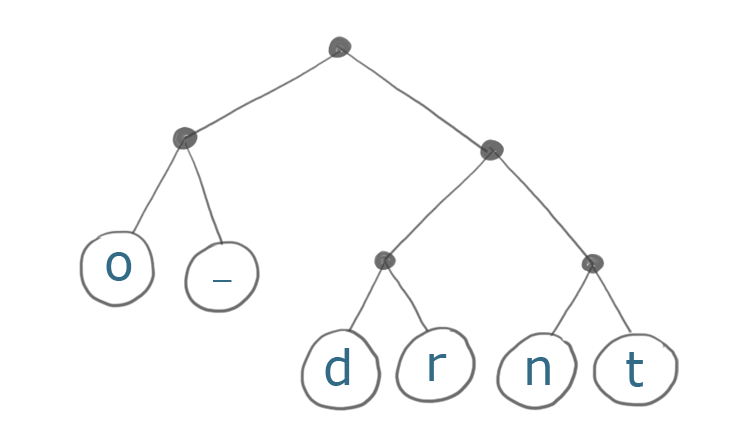
Наиболее распространенные символы в нашей строке - это «о» (4 раза) и пробелы (3 раза). Обратите внимание, что путь к этим символам находится всего в двух шагах от корня по сравнению с тремя для наименее распространенного символа ('t').
Теперь вместо сохранения самого символа мы можем сохранить путь к нему.
Мы начинаем с корневого узла и продвигаемся вниз по дереву к символу, который хотим закодировать. Мы будем хранить 0, если пойдем по левому пути, и 1, если пойдем по правому.
Вот как мы будем кодировать первый символ d, используя это дерево:
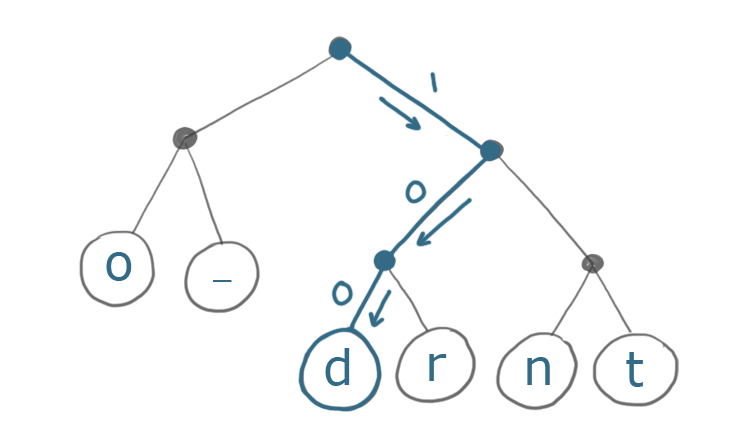
Конечный результат 100 - 3 бита вместо 8. Это существенное улучшение!
Вся закодированная строка выглядит так:

Это 29 бит вместо 96 без потери данных. Круто!
Расшифровка нашей строки
Чтобы декодировать наш текст, мы просто следуем за каждым 0 (левая ветвь) или 1 (правая ветвь), пока не дойдем до символа. Мы записываем этот символ, а затем снова начинаем сверху:
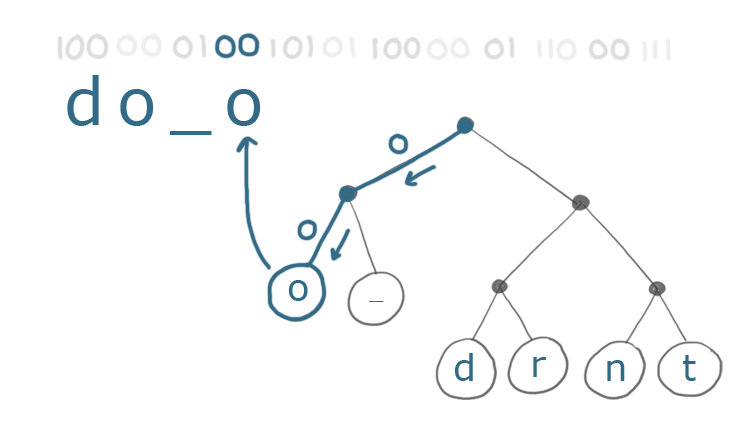
Отправка закодированного текста
Но подождите ... когда мы отправляем закодированный текст кому-то другому, разве им тоже не нужно дерево? Да! Другой стороне нужно такое же дерево Хаффмана для правильного декодирования текста.
Самый простой, но наименее эффективный способ - просто отправить дерево вместе со сжатым текстом.
Мы также могли бы сначала договориться о дереве, и оба использовали бы это дерево при кодировании или декодировании любой строки. Это работает нормально, когда мы можем заранее предсказать распределение символов и можем построить относительно эффективное дерево, не видя сначала конкретной вещи, которую мы кодируем (как, например, с английским текстом).
Другой вариант-отправить ровно столько информации, чтобы другая сторона могла построить то же дерево, что и мы (именно так работает GZIP). Например, мы могли бы отправить общее количество раз, когда встречается каждый символ. Однако мы должны быть осторожны; существует более одного возможного дерева Хаффмана для одного и того же блока текста, поэтому мы должны убедиться, что мы оба строим дерево точно таким же образом.