Идеальная, с бесконечной точностью, игровая физика на Python (серия 2)

Это вторая из нескольких статей, показывающих вам, как запрограммировать идеальный физический движок на Python. Это крошечный шаг в нашем грандиозном стремлении превратить всю физику, математику и даже философию в программирование. Благодаря этому проекту мы откроем для себя сюрпризы, углубим наше понимание и повеселимся. Весь код доступен на GitHub.

В серии 1 мы разработали высший уровень идеального физического движка. Затем мы применили его к колыбели Ньютона, кругу, вписанному в треугольник, а также к теннисному мячу и баскетбольному мячу.

Здесь, в серии 2, мы применим движок к чему-то более сложному: бильярдному брейку.

Представьте, что биток разбрасывает треугольник бильярдных шаров. Если бы — немного позже перерыва — вы могли изменить направление каждого шара, образовали бы они неподвижный треугольник и выплюнули бы биток? Другими словами, есть ли в нашей вселенной кнопка отмены?

Приблизительный физический движок с бабочками

В то время неудача приписывается эффекту бабочки. Эффект бабочки говорит о том, что очень небольшие различия (или приближения) в начальных условиях могут привести к большим различиям позже.

Идеальный физический движок без бабочек

Наш новый физический движок позволяет избежать эффекта бабочки. Он точно знает каждое время, положение и скорость. Он использует такие выражения, как 175–9*sqrt(3)/2. Итак, мы должны иметь возможность перевернуть бильярд, верно? Давайте посмотрим.

Это все еще не работает. Треугольник снова формируется заново, но снова он не остается вместе. Однако, как программисты, мы не впадаем в уныние, мы занимаемся отладкой. В этом случае мы должны отладить мир.

Мы начнем с запуска симуляции событие за событием:

Удивляет ли вас отсутствие симметрии? Как программисты, мы знаем наш следующий шаг отладки: создайте минимально воспроизводимый пример. Другими словами, найдите небольшой пример, который показывает ту же проблему.

Рассмотрим этот мир с тремя кругами. Мы запускаем его дважды.

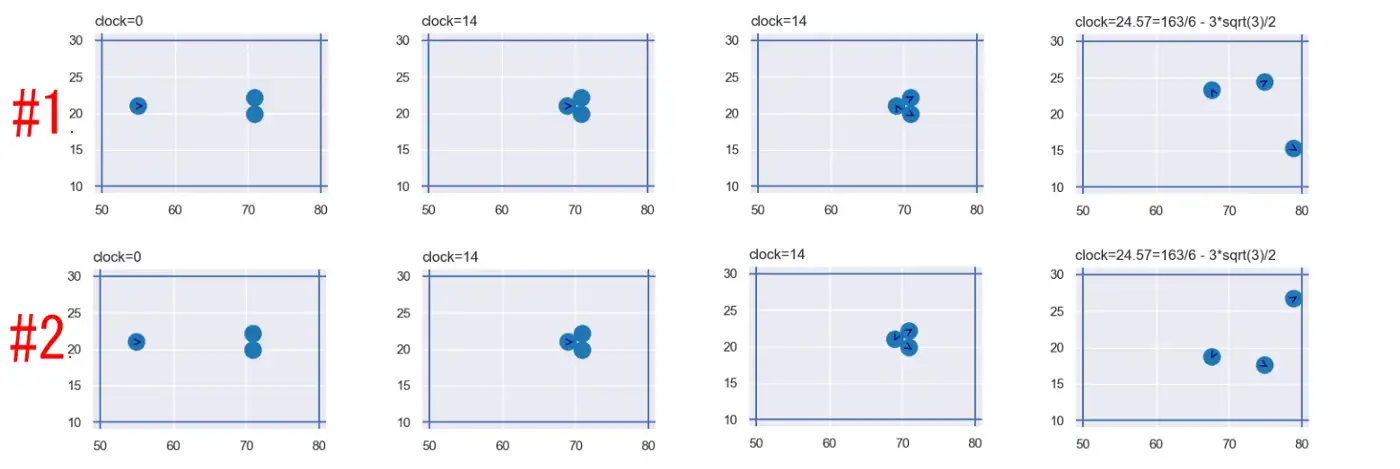
В 3-м фрейме посмотрите на стрелки скорости битков. Стрелки указывают в разных направлениях. Миры разошлись.

Мы можем проследить причину до второго кадра. При clock=14 биток попадает в два других шара. Но в какой мяч он попадает мгновенно первым? Тот, в кого он попадет первым, получит больше энергии, нарушая симметрию.

Почему бы не поддерживать симметрию, распределяя энергию поровну? Ну, потому что …

• Мы обсудили три варианта: максимальная энергия мяча 1, максимальная энергия мяча 2 или равная энергия. Однако в целом симулятор сталкивается с бесконечным континуумом вариантов. Он мог делить энергию между двумя шарами в любой пропорции, сохраняя при этом энергию и импульс. Что делает «равный» особенным?
• В этом случае «равное» может быть оправдано симметрией. Однако в общем случае симметрии не будет. Рассмотрим это асимметричное столкновение между тремя движущимися кругами. Таким образом, симметрия не дает ответа.
  

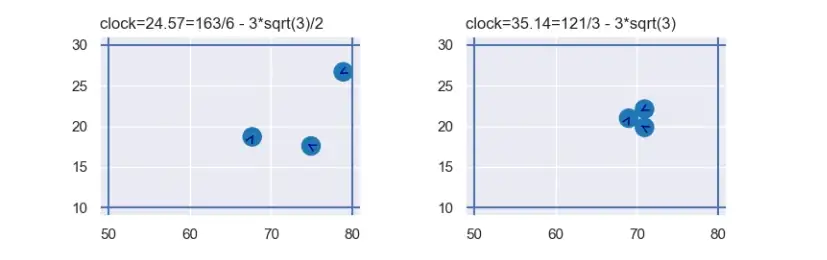
Таким образом, множественные столкновения могут привести к бесконечному количеству возможных результатов, и мы не можем полагаться на симметрию. Что мы можем сделать? Я не думаю, что существует какой-либо «справедливый» способ выбора из бесконечного числа возможных исходов. (Для получения дополнительной информации см. этот комментарий Physics Stack Exchange Сэмми Гербила. Он приходит к такому же выводу и включает ссылки. Также см. это обсуждение 2003 года в группе Google sci.physics.research.)

Если сомневаетесь, сделайте что-нибудь простое. У меня симулятор обрабатывает несколько столкновений как список попарных столкновений. Затем он обрабатывает каждую пару в случайном порядке. Например, когда три окружности — A, B, C — сталкиваются, у нас есть до трех пар столкновений — AB, BC, AC — которые можно упорядочить 3, то есть 6 способами.

Даже этот простой подход приводит к большому количеству возможных результатов. В полном мире бильярда с 15 треугольными шарами движок часто видит столкновения с 5-7 парами (таким образом, от 120 до 5040 исходов). Он также видит одно столкновение с 18 парами (итак, 18! или 6 402 373 705 728 000 исходов).

Проблема столкновения частиц

Это наводит на новый вопрос. Могли бы вы перевернуть бильярдный брейк, если бы вам очень-очень повезло? Считается, что ответ всегда «да», но, как это доказать. Однако для мира с тремя треугольными шарами можно пробовать различные случайные исходники. Семнадцатый исходник сработал, создав это видео:

и это обычное видео:

Таким образом, даже при идеальной физике с бесконечной точностью мир не является детерминированным, если только нам не очень-очень повезло. Этот результат не зависит от эффекта бабочки (небольшие различия приводят к большим различиям) или квантовой неопределенности. Скорее, это зависит от бесконечного числа способов, которыми три или более сталкивающихся объекта могут обмениваться энергией и импульсом, при этом подчиняясь законам ньютоновской физики.

Теперь мы можем ответить на вопрос об обратимости: обратим ли совершенный мир с бесконечной точностью? Мы видели, что на практике ответ «нет».

Удивительно, но физики отвечают «да». Как? Скрытно используя другое определение «обратимости». Насколько я могу судить, говорят, что система «обратима», если есть хоть какой-то шанс вернуться в свое предыдущее состояние, даже если этот шанс равен одному из 6 402 373 705 728 000 или если выбрать одну точку на бесконечном континууме.

Знают ли философы науки об этих проблемах? Процитируем Стэнфордскую философскую энциклопедию:

Подводим итоги

Мир практически необратим! С нашим совершенным физическим движком мы ответили на философский вопрос.

В серии 1 мы разработали высший уровень идеального физического движка и применили его к таким мирам, как теннисный мяч и баскетбольный мяч.

В серии 2, мы начали с попытки заставить бильярдные шары преобразоваться в неподвижный треугольник, а затем выплюнуть биток. Мы можем объяснить эту неудачу эффектом бабочки. Он снова потерпел неудачу с нашим новым совершенным физическим движком. Используя наши навыки отладки, мы обнаружили, что проблема заключается в недетерминированности множественных столкновений. Только в очень простых мирах и при большой удаче мы когда-либо видим обратимость.

Далее, в серии 3, мы увидим, как заставить компьютер создать две функции Python, лежащие в основе движка.