Как использовать технику Sliding Window — пример алгоритма и решение

Недавно я практиковался в кодировании задач, связанных со структурами данных и алгоритмами, готовясь к смене работы.
Во время этого процесса я столкнулся с техникой скользящего окна. Этот алгоритм показался мне очень интересным, поэтому я хотел поделиться своими знаниями с сообществом.
Это руководство будет полезно для вас, если вы готовитесь к собеседованиям по конкурсному программированию. Итак, начнем.
Что такое техника скользящего окна?
Метод скользящего окна — это алгоритмический подход, используемый в информатике и обработке сигналов. Он включает в себя выбор подмножества фиксированного размера или «окна» из большего набора данных и поэтапное перемещение этого окна по набору данных.
Окно перемещается по данным, обычно по одному элементу за раз, и на каждом этапе выполняет некоторую операцию над элементами внутри окна.
Вы растеряны? Позвольте мне подробно описать эту технику на примере.
Пример скользящего окна
Предположим, вы занимаетесь соревновательным программированием и столкнулись со следующей проблемой:
«Найдите максимальную сумму подмассива размера k с временной сложностью O(N).
Array = [1, 2, 6, 2, 4, 1], k = 3"Если вы не знакомы с концепцией временной сложности, вот краткое определение:
В теоретической информатике временная сложность — это вычислительная сложность, которая описывает количество компьютерного времени, необходимое для запуска алгоритма.
И вот курс, если вы хотите узнать больше.
Вернемся к нашей проблеме. По сути, нам нужно найти подмассив размером 3, сумма которого является максимальной (наибольшее число). Вот наглядное представление того, как мы можем решить эту проблему:
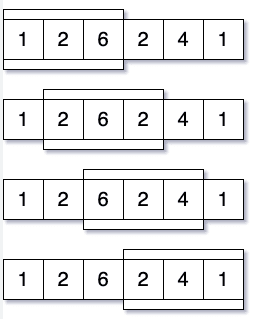
Ручное решение
Давайте решим это вручную. Из изображения выше давайте найдем сумму каждого из подмассивов размера 3.
- Сумма первого подмассива = 1 + 2 + 6 = 9
- Сумма второго подмассива = 2 + 6 + 2 = 10
- Сумма третьего подмассива = 6 + 2 + 4 = 12
- Сумма 4-го подмассива = 2 + 4 + 1 = 7
Максимальное (самое большое) число среди 9, 10, 12 и 7 равно 12 – или третьему подмассиву. Это наше решение.
Решение кода
Хорошо, давайте наденем обувь программирования и попробуем решить эту проблему с помощью кода.
Вот мое решение проблемы:
function findMaxSumOfSequence(listOfItems: number[], sequenceLength: number) {
if (listOfItems.length < sequenceLength) {
return null;
}
let maxSum = -Infinity;
for (let i = 0; i <= listOfItems.length - sequenceLength; i++) {
let sum = 0;
for (let j = i; j < i + sequenceLength; j++) {
sum += listOfItems[j];
}
maxSum = Math.max(maxSum, sum);
}
return maxSum;
}
const input = [1, 2, 6, 2, 4, 1],
windowSize = 3;
console.log(
`Maximum sum of a sub-array of window size ${windowSize} is ${findMaxSumOfSequence(
input,
windowSize
)}`
);Вот краткий обзор приведенного выше кода.
Я определяю входной массив и размер окна внизу и вызываю метод findMaxSumOfSequence с этими параметрами.
Сначала я проверяю, превышает ли размер входного массива размер окна, иначе расчет невозможен, поэтому возвращаю ноль.
Я предполагаю, что максимальная сумма равна минус бесконечности.
Я перебираю массив и для каждого элемента массива перебираю следующие k элементов, нахожу их сумму и присваиваю текущую сумму окна переменной максимальной суммы, если текущая сумма окна больше существующей максимальной суммы. Наконец, верните максимальную сумму.
Попробуем запустить код

Вот так. Мы получили правильный ответ.
Но на этом проблема не заканчивается. Если внимательно посмотреть на проблему, то нам придется найти решение с временной сложностью O(N).
Итак, вы можете задаться вопросом, какова временная сложность приведенного выше решения. Что ж, временная сложность приведенного выше решения равна O(N*k). Это означает, что мы повторяем k раз для каждого элемента массива (вложенный цикл for).
Временная сложность O(N) в основном означает, что вам нужно найти максимальное значение, перебирая заданный массив только один раз.
Использование техники скользящего окна
Как решить эту проблему за одну итерацию? Здесь в игру вступает техника раздвижных окон. Давайте еще раз посмотрим на графическое представление нашего решения:

Здесь вы можете заметить, что окно скользит по массиву. Первоначально он охватывает индексы 0, 1 и 2 в первом подмассиве. Для следующего подмассива он сдвигается на одну позицию вправо, удаляя 0-й индекс слева и добавляя 3-й индекс справа. Итак, теперь он охватывает 1, 2 и 3 во втором подмассиве... и так далее.
Для подмассивов расчет происходит следующим образом:
- 1-й подмассив = 1 + 2 + 6 = 9
- 2-й подмассив = 9 (сумма 1-го подмассива) – 1 + 2 = 10
Давайте посмотрим на это внимательно. Мы находим, что сумма 1-го подмассива равна 9. Чтобы вычислить сумму 2-го подмассива, мы вычитаем выходящее число (1 в 0-м индексе) и добавляем входящее число (2 в 3-м индексе).
- 3-й подмассив = 10 (сумма 2-го подмассива) – 2 + 4 = 12
- 4-й подмассив = 12 (сумма 3-го подмассива) – 6 + 1 = 7
Это техника скользящего окна. Следуя этому методу, мы сможем найти сумму максимального подмассива за одну итерацию.
Как реализовать скользящее окно в коде
Хорошо, давайте снова наденем обувь для кодирования и попробуем реализовать это.
function findMaxSumOfSequence(listOfItems: number[], sequenceLength: number) {
if (listOfItems.length < sequenceLength) {
return null;
}
let start = 0,
end = 0,
maxSum = 0,
windowSum = 0;
while (end < sequenceLength) {
windowSum += listOfItems[end];
end++;
maxSum = windowSum;
}
while (start + sequenceLength < listOfItems.length) {
windowSum = windowSum - listOfItems[start] + listOfItems[end];
maxSum = Math.max(windowSum, maxSum);
start++;
end++;
}
return maxSum;
}
const input = [1, 2, 6, 2, 4, 1],
windowSize = 3;
console.log(
`Maximum sum of a sub-array of window size ${windowSize} is ${findMaxSumOfSequence(
input,
windowSize
)}`
);Давайте попробуем разобраться в приведенном выше коде. Я внес некоторые изменения в метод findMaxSumOfSequence. Я ввел начальные и конечные переменные, которые описывают оконный блок.
В этой реализации у нас есть два цикла, но они не вложены. Это потому, что в первом цикле нам нужно найти сумму первого окна. Второй цикл вычитает и добавляет элементы из результата первого цикла.
В приведенном выше примере первый цикл будет перебирать первые k элементов (3), то есть 1, 2 и 6. Я вычисляю сумму и сохраняю ее в переменных maxSum и windowSum.
В следующем цикле я перебираю каждый элемент массива. Для каждого элемента я вычитаю предыдущее число, добавляю следующее число и обновляю результат в переменной windowSum. Я сравниваю переменные windowSum и maxSum и обновляю переменную maxSum, если windowSum больше. Затем я перемещаю окно в следующий подмассив, увеличивая начальную и конечную переменные. Наконец, я возвращаю максимальную сумму.
Вот вывод приведенного выше кода:

С помощью этой реализации мы удовлетворили требование задачи, пройдя по массиву только один раз и найдя максимальную сумму подмассива (с временной сложностью O(N)).
Применение техники скользящего окна
Техника скользящего окна универсальна и находит применение в различных областях.
Манипуляции с массивами и строками. При обработке массивов или строк скользящее окно можно использовать для эффективного выполнения таких операций, как поиск подмассивов или подстрок, удовлетворяющих определенным условиям.
Сжатие данных. Алгоритмы сжатия скользящего окна, такие как LZ77 и его варианты, используют окно для поиска повторяющихся шаблонов во входных данных и заменяют их ссылками на предыдущие вхождения.
Обработка изображений. При обработке изображений скользящее окно можно использовать для таких задач, как извлечение признаков, обнаружение объектов или сегментация изображения.
Обработка сигналов. Данные временных рядов можно анализировать с использованием скользящего окна для выявления локальных закономерностей, тенденций или аномалий.
Сетевые протоколы. Протоколы скользящего окна используются в компьютерных сетях для надежной и эффективной передачи данных. Отправитель и получатель поддерживают окно допустимых порядковых номеров для управления потоком данных.
Заключение
Надеюсь, после просмотра этих примеров у вас теперь есть четкое представление о том, как работает техника скользящего окна. Я бы порекомендовал вам попробовать решить некоторые другие задачи с помощью этой техники, чтобы ознакомиться с ней. Попытка найти минимальную сумму подмассива размера k самостоятельно, используя этот метод, будет полезным упражнением.
Как я упоминал ранее, я активно пытаюсь сменить работу. Если у вас есть хорошая вакансия в вашей организации, направьте меня.
Надеюсь, вам понравилось читать эту статью. Если вы хотите узнать больше о методах прохождения собеседований по конкурентному программированию, подпишитесь на мою рассылку, посетив мой сайт, где также есть сводный список всех моих блогов.