Масштабируемые Graph преобразователи для миллионов узлов

В последнее время создание моделей Transformer для обработки графоструктурированных данных вызвало широкий интерес в сообществе исследователей машинного обучения. Одна из критических проблем связана с квадратичной сложностью глобального внимания, которая мешает трансформерам масштабироваться до больших графов. В этом блоге будет кратко представлена ​​недавняя работа над NeurIPS22:

В этой работе предлагается масштабируемый graph Transformers для графов классификации больших узлов, где количество узлов может варьироваться от тысяч до миллионов (или даже больше). Ключевой модуль представляет собой передачу сообщений на основе ядра Gumbel-Softmax, которая обеспечивает распространение функций по всем парам со сложностью O(N) (N для #nodes).

Нижеследующее содержание подытожит основную идею и результаты данной работы.

Graph Transformers против Graph Neural Networks

В отличие от graph neural networks (GNN), которые прибегают к передаче сообщений по фиксированной топологии входного графа, graph Transformers могут более гибко агрегировать глобальную информацию со всех узлов посредством адаптивной топологии на каждом уровне распространения. В частности, графовые трансформеры имеют ряд преимуществ:

• Работа с несовершенными структурами. Для графовых данных с гетерофильностью, дальней зависимостью и ложными краями GNN часто показывает недостаточную мощность из-за своих схем агрегации локальных признаков. Тем не менее, Transformers привлекают внимание всего мира, объединяя информацию со всех узлов на одном уровне, что позволяет преодолеть ограничения входных структур.
• Избегайте чрезмерного раздавливания. GNN могут экспоненциально терять информацию при агрегировании информации в вектор фиксированной длины, в то время как graph Transformers используют глобальное внимательное агрегирование, которое может адаптивно обслуживать доминирующие узлы, которые являются информативными для задач прогнозирования целевого узла.
  
• Гибкость для задач No-Graph. Помимо задач с графами, существует множество задач, в которых отсутствует структура графа. Например, классификация изображений и текста (каждое изображение можно рассматривать как узел, но нет соединяющего их графа) и моделирование физики (каждая частица является узлом, но нет явно наблюдаемого графа). Хотя общепринятой практикой является использование k-NN поверх входных признаков для построения графа подобия для передачи сообщений, такой искусственно созданный граф часто не зависит от последующих задач прогнозирования и может привести к неоптимальной производительности. Transformers решает эту проблему, позволяя автоматически изучать адаптивные структуры графов для передачи сообщений.
  

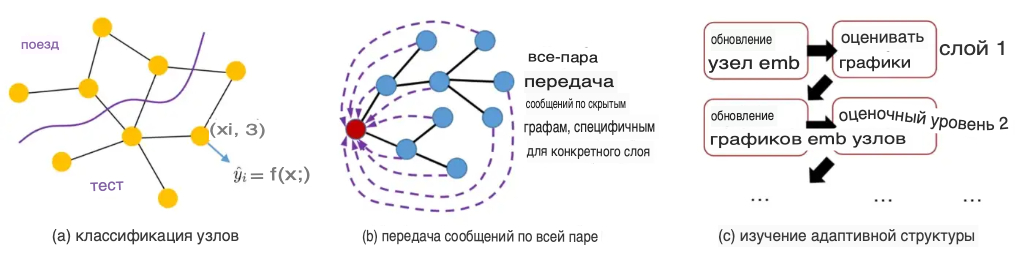
Проблемы построения Transformers на Large Graphs

Несколько проблем делают нетривиальной задачу построения трансформеров на больших графах, особенно тех, которые содержат более тысячи узлов.

• Квадратичная сложность для глобального внимания: вычисление внимания для агрегации всех пар функций требует сложности O(N²), что является недопустимым для больших графов, где N может быть произвольно большим, например, от тысяч до миллионов. Конкретно говоря, обычный графический процессор с 16 ГБ памяти не сможет обеспечить такое глобальное внимание ко всем узлам, если N больше 10 КБ.
• Аккомпанемент разреженности графа: Реальные графы часто бывают разреженными по сравнению с внимательным графом (мы можем рассматривать матрицу внимания как взвешенную матрицу смежности графа), которые плотно соединяют все пары узлов. Проблема в том, что когда N становится большим, распространение признаков по такому плотному графу может вызвать то, что мы называем проблемой чрезмерной нормализации, что означает, что информация из разных узлов разбавляется другими. Вероятное средство для разреживания обучаемых структур перед распространением.
  

Ядро передачи сообщений на основе Gumbel-Softmax

Наша работа NodeFormer сочетает случайную карту признаков и Gumbel-Softmax в качестве единой модели для решения вышеупомянутых проблем. В частности, Gumbel-Softmax впервые используется для замены исходной агрегации внимательных функций на основе Softmax:

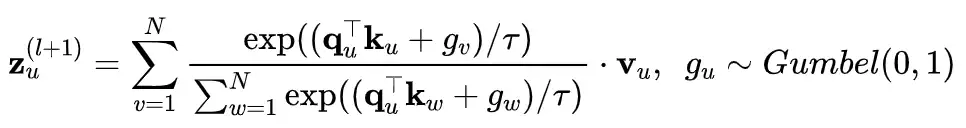
Приведенное выше уравнение определяет вычисление для узла u, которое требует O(N), а для вычисления представлений для N узлов требуется сложность O(N²), поскольку необходимо независимо вычислять оценки внимания для всех пар. Чтобы решить эту трудность, мы прибегаем к основной идее в Performer и применяем карту случайных признаков (RFM) для аппроксимации Gumbel-Softmax (первоначальное внедрение RFM в Performer направлено на аппроксимацию детерминированного внимания Softmax, и здесь мы расширяем такую ​​технику в Gumbel-Softmax со стохастическим шумом).

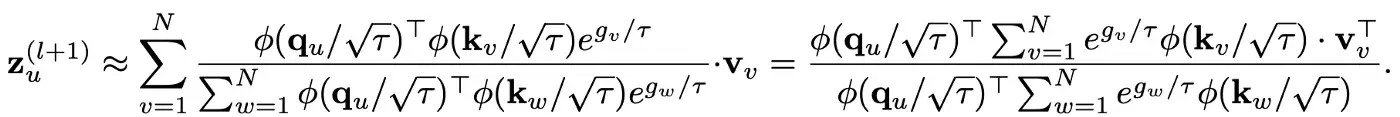
Важно отметить, что в новом вычислении, то есть в правой части приведенного выше уравнения, два члена суммирования (по N узлам) являются общими для всех узлов и могут быть вычислены только один раз в одном слое. Следовательно, это приводит к сложности O(N) для обновления N узлов на одном уровне.

Как использовать входные графы

Еще один важный вопрос заключается в том, как использовать входные структуры (если они доступны), поскольку описанная выше передача сообщений по всем парам игнорирует входной граф. Мы дополнительно предлагаем две простые стратегии:

1. Добавление реляционного смещения: мы дополнительно предполагаем обучаемый скалярный термин, который добавляется к оценке внимания между узлами u и v, если во входном графе между ними есть ребро.
2. Потеря регуляризации Edge: используйте оценку внимания для края (u, v) в качестве предполагаемой вероятности и определите потерю оценки максимального правдоподобия (MLE) для всех наблюдаемых краев. Интуитивно понятно, что этот дизайн максимизирует вес внимания для наблюдаемых краев.
   

Но важность (или, скажем, информативность) входного графа различается для разных наборов данных. Таким образом, на практике необходимо настроить вес (как гиперпараметр), который определяет, сколько внимания уделяется входным графам. На следующем рисунке показан общий поток данных NodeFormer.

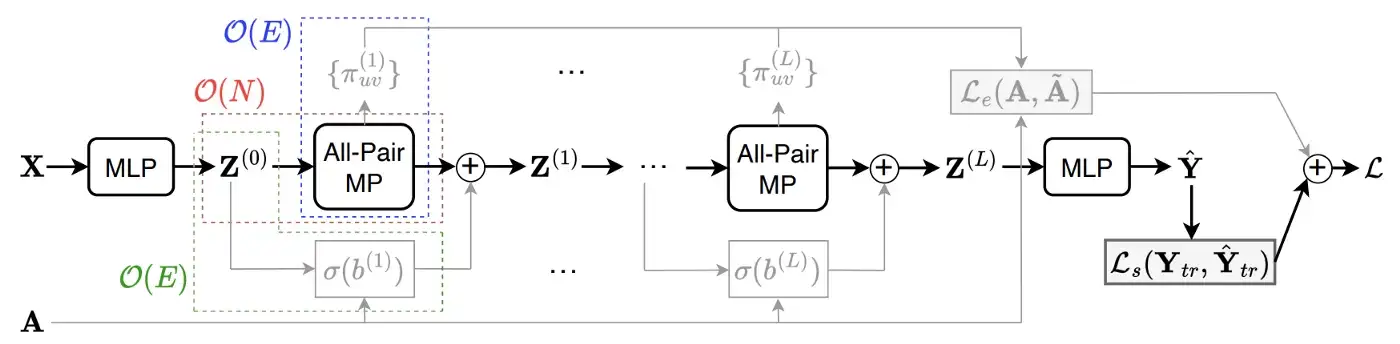
Результаты эксперимента

Мы применяем NodeFormer для задач классификации узлов и достигаем очень конкурентоспособных результатов на восьми наборах данных по сравнению с обычными GNN и современными моделями обучения структуры графа LDS и IDGL.

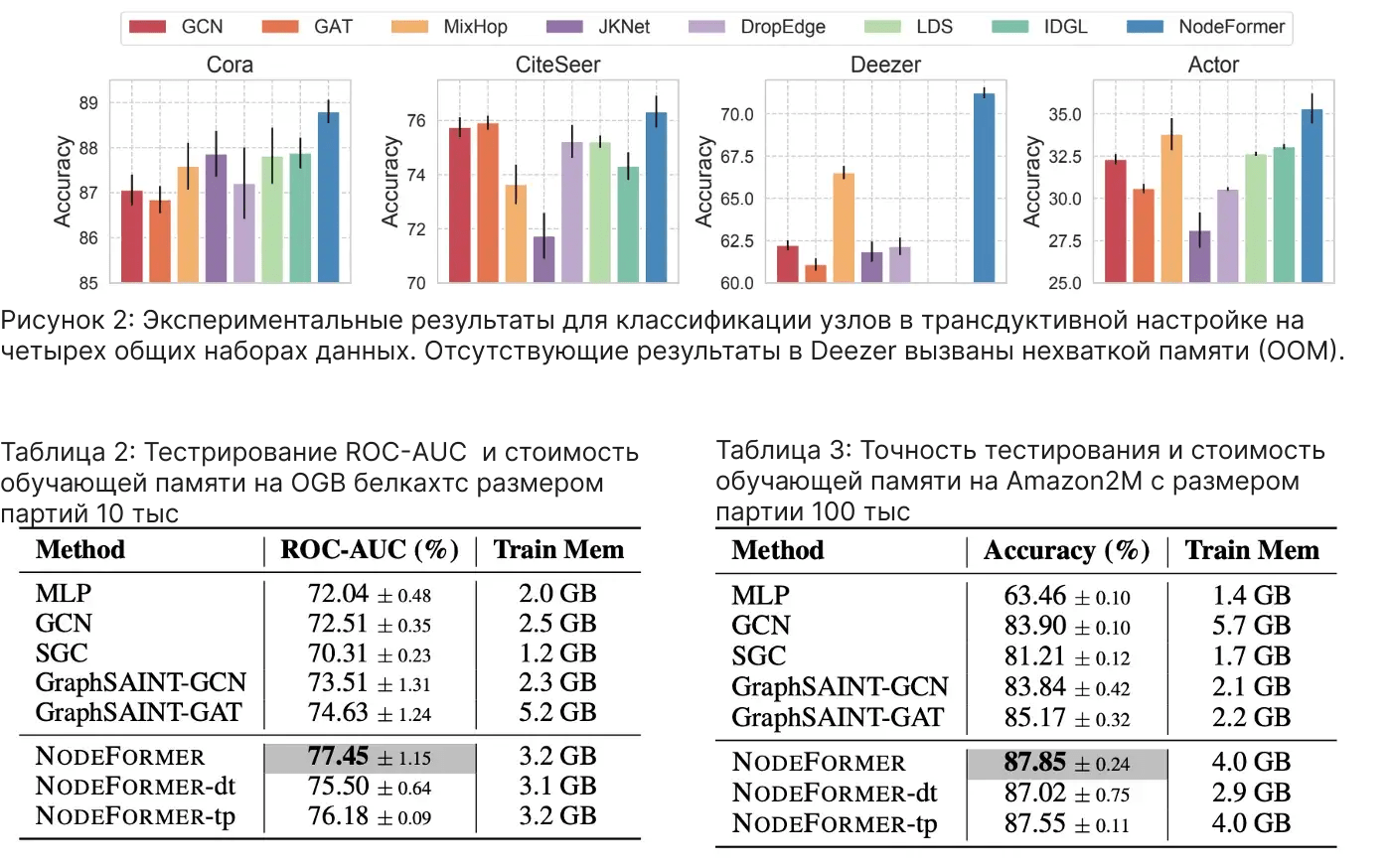
Помимо классификации узлов, мы также рассматриваем задачи классификации изображений и текста, в которых отсутствуют входные графы. Мы используем k-NN с разными значениями k (5, 10, 15, 20) для построения графа, а также рассматриваем возможность отказа от использования входного графа для NodeFormer. Интересно, что последний случай не приводит к явному падению производительности, а иногда может повысить производительность.

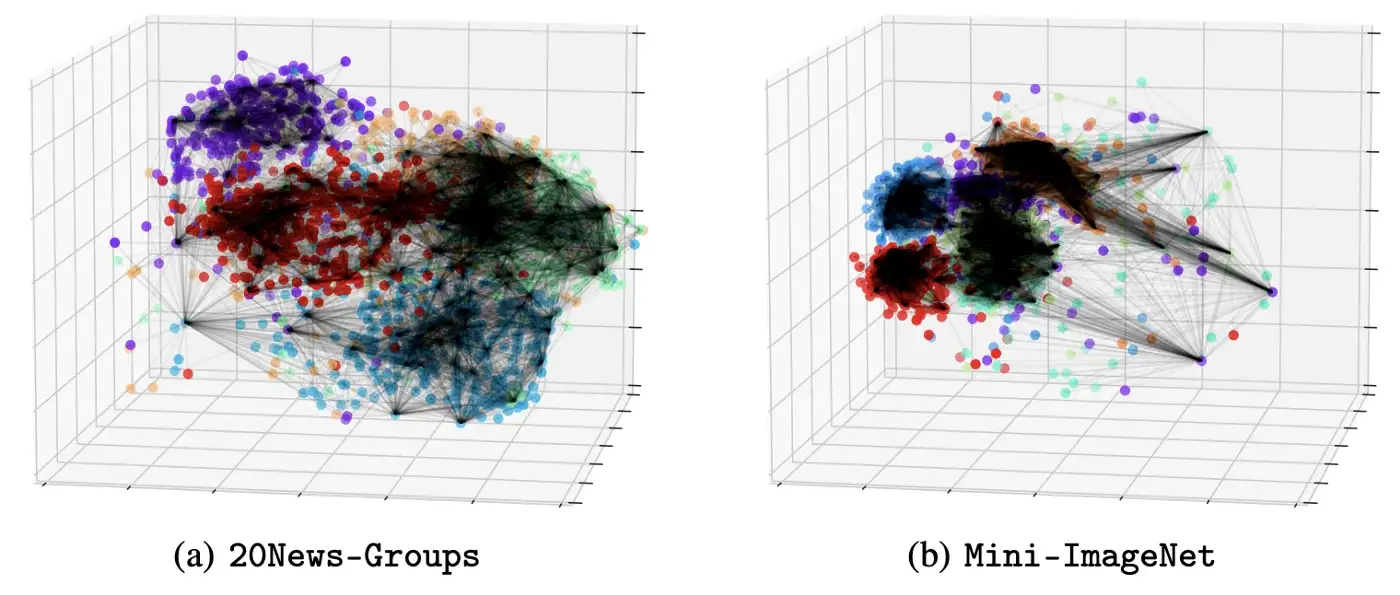
Здесь мы выделяем некоторые преимущества NodeFormer:

• Емкость: NodeFormer адаптивно изучает структуру графа за счет разреженного внимания на каждом уровне и потенциально собирает информацию со всех узлов.
• Масштабируемость: NodeFormer обеспечивает сложность O(N) и мини-пакетное обучение разделов. На практике он успешно масштабируется до больших графов с миллионами узлов, используя всего 4 ГБ памяти.
  
• Эффективность: обучение NodeFormer может быть эффективным сквозным способом с оптимизацией на основе градиента. Например, обучение и оценка Cora в 1000 эпох занимает всего 1–2 минуты.
  
• Гибкость: NodeFormer гибок для индуктивного обучения и обработки случаев отсутствия графа.
  

В этом блоге представлены новые преобразователи графов, которые успешно масштабируются до больших графов и демонстрируют многообещающую производительность по сравнению с обычными GNN. Модели в стиле Transformer обладают некоторыми неотъемлемыми преимуществами, которые могут преодолеть ограничения GNN в отношении обработки зависимости дальнего действия, гетерофилии, чрезмерного сжатия, графического шума и полного отсутствия графов. Несмотря на это, создание мощных преобразователей графов, которые могут служить моделью представления графов следующего поколения, все еще остается открытой и недостаточно изученной проблемой, и мы надеемся, что эта работа может пролить свет на это направление.