Моделирование времени ожидания Starbucks с использованием цепей Маркова с помощью Python

Можно с легкостью сказать, что нас окружает большое количество людей для которых кофе - это религия. Они пьют кофе, чтобы пообщаться, пьют кофе для того, чтобы проснуться утром, пьют кофе после обеда и ужина, перед сном. Когда вы давно не видели друг друга, вы говорите: "Выпьем по чашечке кофе".
А существуют люди с другим подходом к напитку. Они пьют кофе по пути на работу, пьют кофе, когда работают, пока смотрят фильм. И в итоге у них уходит много времени на один стаканчик кофе. А ведь существуют различные виды кофе!
Если вы зайдете в Starbucks, вы увидите, может быть, сотню возможных вариантов кофе, которые вы можете получить. Это может быть черный, это может быть маккиато, это может быть латте, это может быть фраппучино, это может быть много других вещей, названия которых вы ни разу и не слышали.
Есть несколько очень простых в приготовлении чашек кофе, а есть более сложные, для приготовления которых требуется больше времени. Допустим, вы стоите в очереди за кофе в Starbucks. Если перед вами 3 человека, и все они заказывают черный кофе, вам, вероятно, придется подождать около 3 минут, прежде чем получить свой заказ.
Тем не менее, если они закажут «дополнительный карамельный макиато со взбитыми сливками, посыпкой и корицей с соевым молоком»… ну, это может удвоить время ожидания или, по крайней мере, вам придется подождать пару лишних минут.
Итак, вопрос: «Сколько времени мне нужно ждать, прежде чем я получу свой кофе?»
Конечно, мы понятия не имеем, что собираются заказывать другие люди, так что это вероятностная задача (или стохастический процесс).
Выполнимый подход состоит в том, чтобы построить цепь Маркова. В частности, нам понадобится Time-Dependent Markov Chain.
Теоретическое введение
Давайте начнем с теоретического ознакомления с проблемой и ее правильного решения. Начнем с самого простого случая. Мы заходим в Starbucks и должны заказать кофе. Скажем с математической точки зрения, мы можем находиться в одном из этих трех состояний.
Первое состояние (O) - это состояние, в котором мы заказываем кофе. Второе (M) - это то, где мы заказали уже кофе и ждем, когда его принесут. Это потому, что они готовят чашку кофе. Затепм вы получаете кофе и переходите в состояние ухода (L). Это означает, что ваш кофе готов и вы готовы к работе.

Каковы возможные переходы:
- Переход от заказа к изготовлению (От О до М);
- Переход от М к М (продолжать ждать);
- Переход от М к L.
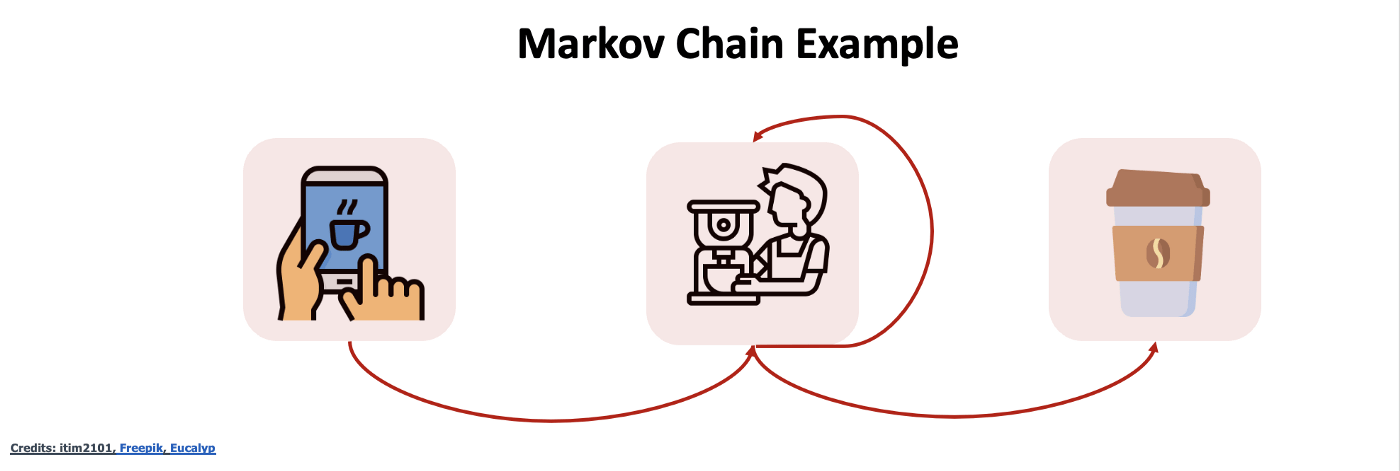
Цепи Маркова
Предположение о цепях Маркова заключается в следующем:
«Вероятность оказаться в следующем состоянии зависит только от вашего текущего состояния»
Например:
Вероятность нахождения в состоянии выхода на временном шаге t = 5 зависит только от того факта, что вы находитесь в состоянии выхода на временном шаге t = 4.
Давайте оформим это:

В приведенных выше значениях мы имеем, что вероятность нахождения в момент времени t в пространстве s_t (O, M, L) зависит только о состояния, в котором мы находимся в момент времени t-1.
В нашем конкретном эксперименте нам нужно помнить, что эта вероятность также должна зависеть от времени. Это так, потому что, если я подождал 5 минут, вероятность уйти в следующую минуту выше, чем вероятность уйти, если бы я ждал всего 1 минуту.
Это означает, что:

Так выглядит та концепция, о которой мы говорили ранее.
Теперь рассмотрим пример, при котором в Starbucks будем не только мы, но и другие клиенты. Усложним эту настройку. Но то, что вы видите выше, является отправной точкой для всех наших действий.
Пример «Один клиент — один напиток»
Приведем самый простой из возможных примеров. Мы знаем какой напиток заказать и мы единственные в кофейне.
Допустим, мы хотим карамельный макиато. Все рецепты предполагают, что это займет 5 минут. Допустим на заказ и оплату уходит 30 секунд. Таким образом, общее время ожидания составит 5 мин 30 сек. Но пойдем дальше. Допустим, 5 минут - это среднее время начала. Давайте также предположим, что мы могли бы приготовить наш кофе за 4 мин или за 6.
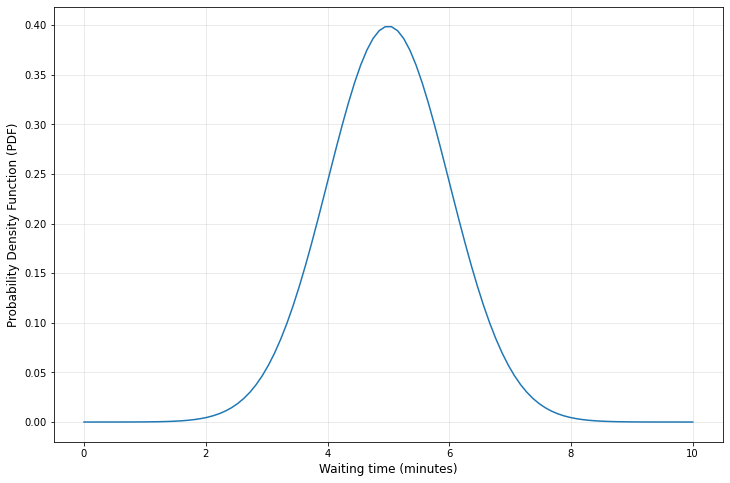
Теперь предположим, что наша временная отметка составляет 30 секунд (0,5 минуты). К сожалению, через 30 секунд у нас будет наш карамельный макиато. Через 8 минут, к сожалению, мы все еще будем ждать.
Практическая реализация
Давайте реализуем наш проект, начнем с импорта некоторых библиотек:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy import signal
import sklearn
import seaborn as snsОпределим наши состояния:
customer_state = ['Ordering the coffee','Waiting for your coffee','Leaving']
states = {'O':customer_state[0],'M':customer_state[1],'L':customer_state[2]}Теперь запустим весь процесс описанный выше. И мы сделаем это с помощью функции:
mu, sigma = 5,1
def one_drink_one_cust():
start = states['O']
print(start+'\n')
ordering_time = 0.5
first_state = states['M']
print(first_state+'\n')
waiting_time = 0
k = 0
while k == 0:
p = stats.norm.cdf(waiting_time, loc=mu, scale=sigma)
k = np.random.choice([0,1],p = [1-p,p])
waiting_time = waiting_time+0.5
if k == 0:
print('Coffee is brewing... \n')
print('Your coffee is ready! \n')
print(states['L']+'\n')
print('Waiting time is = %.2f'%(waiting_time))
return waiting_timeЭто один из примеров:
Ordering the coffee
Waiting for your coffee
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Your coffee is ready!
Leaving
Waiting time is = 3.50
3.5Пример «Один клиент - несколько наименований напитков»
Теперь увеличим сложность модели и сделаем ее более реалистичной. Допустим, мы не знаем, что именно захочет конкретный клиент. Это намного реалистичнее, потому что в Starbucks более 150 наименований напитков, и для них может потребоваться разное время ожидания.
Теперь цепь Маркова выглядит следующим образом:
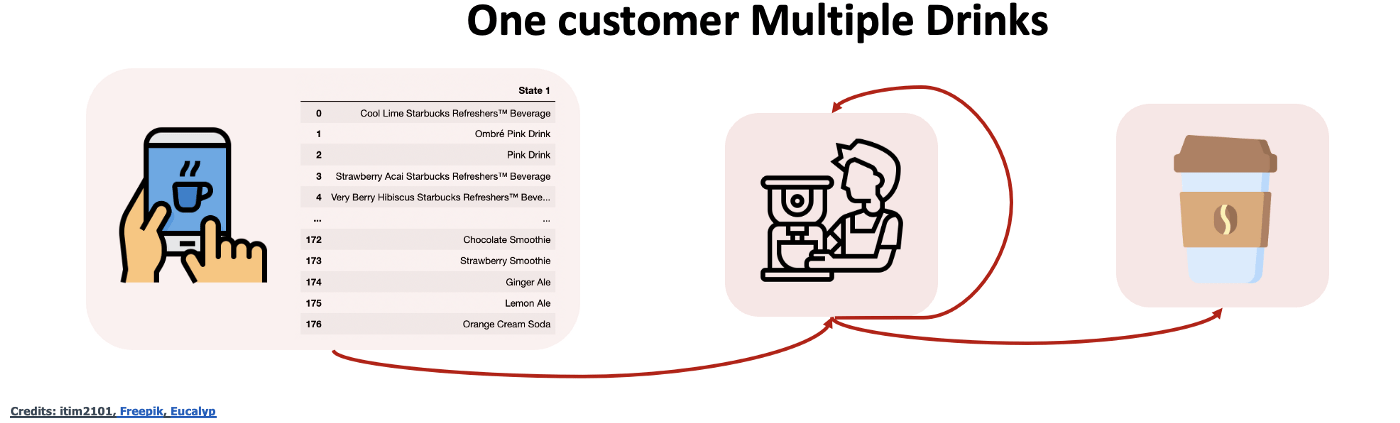
Отличие в предыдущим в том, что у нас есть распределение вероятностей, которое мы назовем:
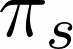
В частности, это распределение вероятностей по всем возможным напиткам, которые мы можем получить, и назовем:
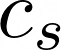
Например:

Так что мы можем сказать:

Практическая реализация
Из этого набора данных Kaggle (CC0: Public Domain) мы можем импортировать все напитки Starbucks:
pd.read_csv('starbucks-menu-nutrition-drinks.csv')| Unnamed: 0 | Calories | Fat (g) | Carb. (g) | Fiber (g) | Protein | Sodium | |
| 0 | Cool Lime Starbucks Refreshers™ Beverage | 45 | 0 | 11 | 0 | 0 | 10 |
| 1 | Ombré Pink Drink | - | - | - | - | - | - |
| 2 | Pink Drink | - | - | - | - | - | - |
| 3 | Strawberry Acai Starbucks Refreshers™ Beverage | 80 | 0 | 18 | 1 | 0 | 10 |
| 4 | Very Berry Hibiscus Starbucks Refreshers™ Beve... | 60 | 0 | 14 | 1 | 0 | 10 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 172 | Chocolate Smoothie | 320 | 5 | 53 | 8 | 20 | 170 |
| 173 | Strawberry Smoothie | 300 | 2 | 60 | 7 | 16 | 130 |
| 174 | Ginger Ale | - | - | - | - | - | - |
| 175 | Lemon Ale | - | - | - | - | - | - |
| 176 | Orange Cream Soda | - | - | - | - | - | - |
Другие столбцы нам не нужны. Сейчас мы не знаем, какой напиток самый популярный, поэтому просто сделаем фейковую раздачу для наших целей:
kind_of_coffee = np.array(pd.read_csv('starbucks-menu-nutrition-drinks.csv')['Unnamed: 0'])
p_start = []
for i in range(len(kind_of_coffee)):
p_start.append(np.random.choice(np.arange(50,100)))
p_start = np.array(np.array(list(np.array(p_start)/sum(p_start))))Итак, мы извлекаем значения от 50 до 100, затем нормализуем их, используя сумму, чтобы у нас был вектор вероятности.
coffe_picked = []
for i in range(10000):
coffe_picked.append(np.random.choice(range(0,len(kind_of_coffee)),p=p_start))
sns.displot(coffe_picked)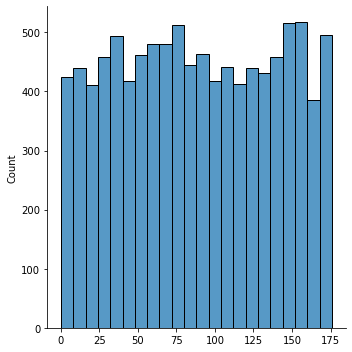
У нас теперь есть распределение вероятностей, и что же следует далее? Это распределение вероятностей сделает для нас заказ: мы просто сделаем выборку из распределения. Тогда мы должны предположить, что каждый кофе требует разного времени для приготовления.
Сейчас разница не так уж и велика. Допустим, это займет в среднем 3 минуты для «самого простого» кофе (предположим, это будет американо) и 6 минут (в среднем) для самого сложного кофе, который нужно приготовить (и в нашем случае, карамельный макиато со взбитыми сливками с посыпкой и корицей с соевым молоком).
Также мы поиграем с различными отклонениями (от 0,1 до 1).
coffee_data = pd.DataFrame(kind_of_coffee,columns=['State 1'])
mu_list = []
var_list = []
for i in range(len(coffee_data)):
mu_list.append(np.random.choice(np.linspace(3,6,1000)))
var_list.append(np.random.choice(np.linspace(0.1,1.5,1000)))
coffee_data[r'$\mu$']=mu_list
coffee_data[r'$\sigma$']=var_list
coffee_data[r'$p$'] = p_start
coffee_data.head()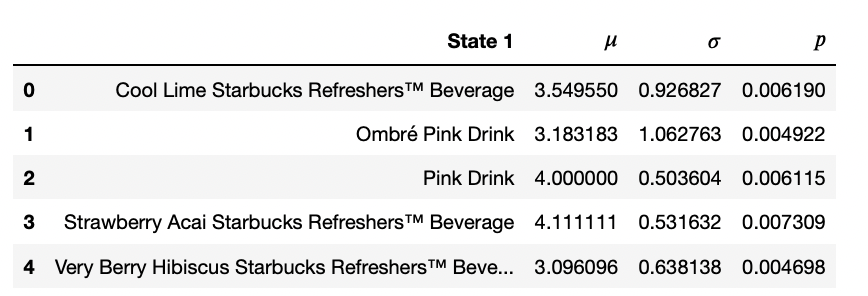
Как мы видели ранее, у нас есть среднее значение, которое может варьироваться от 3 до 6, так, что у вас может быть среднее время ожидания, которое может составлять от 3 до 6 минут, и бывает, что иногда бывает, что у вас больше неопределенности, чем в других случаях. Например, у вас самая большая дисперсия, когда вы пьете кофе «А».
Реализуем следующую ситуацию:
def random_drink_one_cust():
start = states['O']
print(start+'\n')
ordering_time = 0.5
first_state = states['M']
chosen_i = np.random.choice(range(0,len(kind_of_coffee)),p=p_start)
print('Ordering coffee %s'%(kind_of_coffee[chosen_i]))
print(first_state+'\n')
mu_i, var_i = coffee_data[r'$\mu$'].loc[chosen_i], coffee_data[r'$\sigma$'].loc[chosen_i]
waiting_time = 0
k = 0
while k == 0:
p = stats.norm.cdf(waiting_time, loc=mu_i, scale=var_i)
k = np.random.choice([0,1],p = [1-p,p])
waiting_time = waiting_time+0.5
if k == 0:
print('Coffee is brewing... \n')
print('Your coffee is ready! \n')
print(states['L']+'\n')
print('Waiting time is = %.2f'%(waiting_time))
return waiting_time
random_drink_one_cust()Ordering the coffee
Ordering coffee Teavana® Shaken Iced Black Tea
Waiting for your coffee
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Coffee is brewing...
Your coffee is ready!
Leaving
Waiting time is = 4.00
4.0Теперь на этом этапе мы можем извлечь некоторую значимую информацию. Например:
«Сколько времени обычно требуется, чтобы выпить кофе в Starbucks?»
Этот вопрос довольно общий, поэтому мы могли бы также ответить на некоторые статистические данные*:
waiting_time_list = []
for i in range(10000):
waiting_time_list.append(random_drink_one_cust())
plt.figure(figsize=(20,10))
plt.subplot(2,1,1)
sns.histplot(waiting_time_list,fill=True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel('Waiting time (minutes)',fontsize=14)
plt.ylabel('Count',fontsize=14)
plt.subplot(2,1,2)
sns.kdeplot(waiting_time_list,fill=True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel('Waiting time (minutes)',fontsize=14)
plt.ylabel('Probability Density Function (PDF)',fontsize=14)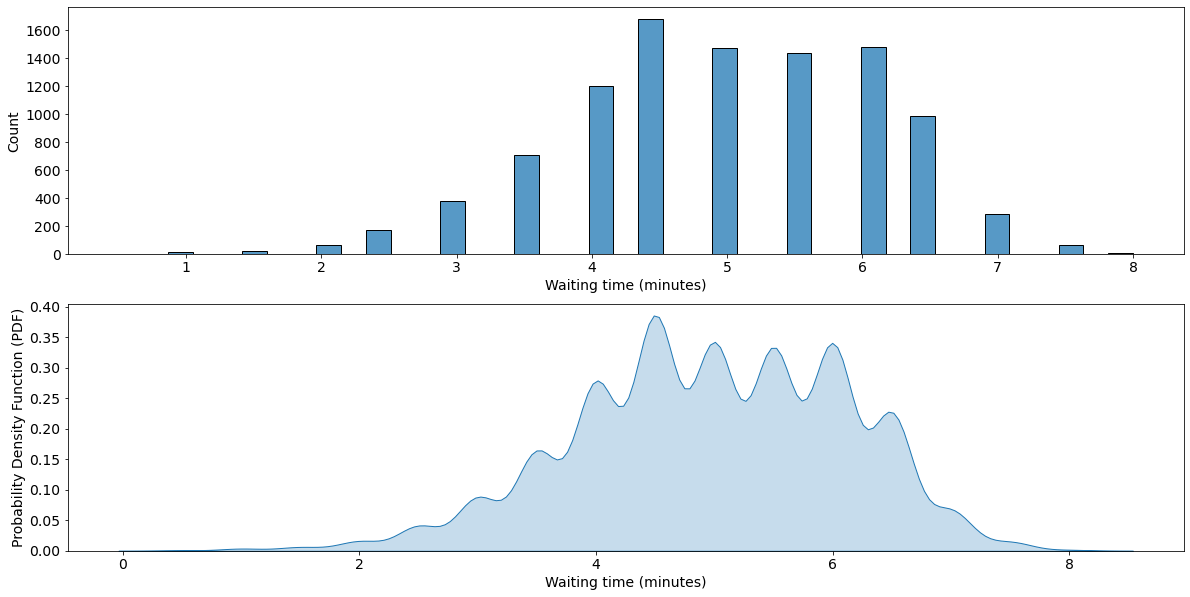
*Немного изменили функцию, удалив всю «print», чтобы компьютер не взорвался.
Пример «Несколько клиентов - несколько наименований напитков»
Теперь мы рассматриваем присутствие некоторого количества клиентов, Ситуация выглядит следующим образом:
Теперь, нереалистично думать, что нам придется ждать, пока сварится один кофе, прежде чем они начнут готовить ваш. Обычно в Starbucks работает 3 или 4 бариста.
Это немного усложняет код, потому что нам нужно отслеживать тот факт, что все бариста на самом деле заняты или нет. По этой причине функция, которую мы рассмотрим, зависит от количества клиентов и количества бариста.
def random_drink_multiple_cust(cust=2,num_baristas =5):
time_of_process = []
baristas = np.zeros(num_baristas)
q = 0
ordering_time = 0
for c in range(cust):
start = states['O']
print('Customer number %i is ordering'%(c))
ordering_time+=0.5
if sum(baristas)!=num_baristas:
print('There is at least one free baristas! :)')
waiting_time = random_drink_one_cust()
time_of_process.append(waiting_time+ordering_time)
baristas[q] = 1
q = q + 1
if len(time_of_process)==cust:
break
if sum(baristas)==num_baristas:
print('All the baristas are busy :(')
print('You have to wait an additional %i minutes until they can start making your coffee' %(min(time_of_process)))
waiting_time = min(time_of_process)+random_drink_one_cust()+ordering_time
baristas[num_baristas-1]=0
time_of_process.append(waiting_time)
q = q-1
if len(time_of_process)==cust:
break
print('The waiting time for each customer is:')
print(time_of_process)
return time_of_processДавайте протестируем случай, когда у нас 4 клиента и 2 бариста.
Customer number 0 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Iced Caffè Americano
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 1 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Iced Skinny Mocha
Waiting for your coffee
Your coffee is ready!
Leaving
All the baristas are busy :(
You have to wait an additional 6 minutes until they can start making your coffee
Ordering the coffee
Ordering coffee Tazo® Bottled Organic Iced Black Tea
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 2 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Starbucks® Bottled Caramel Frappuccino® Coffee Drink
Waiting for your coffee
Your coffee is ready!
Leaving
The waiting time for each customer is:
[7.0, 6.5, 14.0, 5.5]
[7.0, 6.5, 14.0, 5.5]Как вы можете видеть, в первых двух случаях у нас есть свободные бариста, и они ждут, соответственно, семь и 6,5 минут*.
* Обратите внимание! Это не ошибка! Это просто означает, что второй кофе получается быстрее, чем первый кофе + время заказа. Это имеет смысл, если вы подумаете об этом. Если вы заказываете сложный кофе, а я просто латте, я могу ждать меньше, чем вы, даже если вы сделали заказ раньше меня.
Тогда бариста заняты. Так что нам приходится ждать еще 6 минут, прежде чем я смогу сделать заказ. (Я мог бы сделать это более реалистичным и вычесть 1 минуту из времени заказа, но вы правильно поняли идею?)
К моменту заказа четвертого клиента остается один свободный бариста, так что ему не приходится так долго ждать. Он просто ждет 5,5 минут.
Обратите внимание, насколько сложной может стать эта модель и насколько интересной может быть ситуация. Это кейс с 10 клиентами и 5 бариста:
Customer number 0 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Iced Coconutmilk Mocha Macchiato
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 1 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Coffee Frappuccino® Blended Coffee
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 2 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Strawberry Acai Starbucks Refreshers™ Beverage
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 3 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Shaken Sweet Tea
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 4 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Coffee Traveler
Waiting for your coffee
Your coffee is ready!
Leaving
All the baristas are busy :(
You have to wait an additional 5 minutes until they can start making your coffee
Ordering the coffee
Ordering coffee Starbucks® Doubleshot Protein Vanilla
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 5 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Coconutmilk Mocha Macchiato
Waiting for your coffee
Your coffee is ready!
Leaving
All the baristas are busy :(
You have to wait an additional 5 minutes until they can start making your coffee
Ordering the coffee
Ordering coffee Nitro Cold Brew with Sweet Cream
Waiting for your coffee
Your coffee is ready!
Leaving
Customer number 6 is ordering
There is at least one free baristas! :)
Ordering the coffee
Ordering coffee Starbucks® Low Calorie Iced Coffee + Milk
Waiting for your coffee
Your coffee is ready!
Leaving
All the baristas are busy :(
You have to wait an additional 5 minutes until they can start making your coffee
Ordering the coffee
Ordering coffee Tazo® Bottled Lemon Ginger
Waiting for your coffee
Your coffee is ready!
Leaving
The waiting time for each customer is:
[5.5, 5.5, 7.0, 8.0, 6.5, 12.5, 8.5, 12.5, 7.5, 16.0]
[5.5, 5.5, 7.0, 8.0, 6.5, 12.5, 8.5, 12.5, 7.5, 16.0]Рассуждения
В этой статье мы рассмотрели общую проблему времени ожидания в очереди. конечно есть несколько сценариев:
- Мы можем быть единственными в магазине и точно знать, что мы хотим;
- Мы можем быть единственными в магазине и точно не знаем, чего хотим.;
- Нас может быть много в магазине, и мы не знаем точно, чего хотим.
Эти три сценария, конечно, становятся все более и более сложными. По этой причине цепочка Маркова становится все более и более сложной, как мы видели ранее.
- В первом случае единственным распределением вероятностей является распределение «coffee-making» процесса. Например, приготовление нашего карамельного макиато занимает в среднем 5 минут с гауссовым распределением и дисперсией 1.
- Во втором случае у нас есть распределение вероятностей кофе, который мы выбрали, плюс распределение вероятностей этапа приготовления кофе, то есть предыдущего.
- В третьем случае у нас есть и то, и другое, и количество бариста становится еще одним фактором, который следует учитывать.
Конечно, мы могли бы сильно усложнить эту модель. Мы могли бы принять во внимание тот факт, что машины могут быть сломаны. Мы можем рассмотреть вопрос о нехватке бариста. Мы можем учитывать тот факт, что количество бариста меняется со временем. Мы можем считать, что некоторые бариста работают быстрее других. И еще много возможностей.
Эта отправная точка может быть использована для усложнения модели практически всеми способами, которые вы хотите. Просто имейте в виду, что мы используем инструмент зависящей от времени цепи Маркова и просто строим оттуда.