Основная идея реализации бинарного дерева с Golang

Для общих операций алгоритма есть не что иное, как три основные операции записи, поиска и удаления. Кроме того, могут быть некоторые операции, такие как получение информации о соответствующей структуре данных. Например, бинарному дереву может потребоваться получить степень дерева, а стекам и очередям — длину.
Согласно этой идее, нам нужно понять это для работы с бинарным деревом:
- Определение структуры бинарного дерева
- Создание бинарного дерева
- Добавление данных в бинарное дерево
- Подсчитать количество узлов в бинарном дереве
- Вычислить глубину бинарного дерева
- Обход бинарного дерева: четыре метода обхода
- Обход в предварительном порядке: сначала посетите корневой узел, затем посетите левое поддерево и, наконец, посетите правое поддерево; это повторяется до конца.
- Обход в обратном порядке: сначала посетите левое поддерево, затем посетите правое поддерево и, наконец, посетите корневой узел; это повторяется до конца.
- Обход по порядку: сначала посетите левое поддерево, затем посетите корневой узел и, наконец, посетите правое поддерево; это повторяется до конца.
- Иерархический обход: каждый уровень посещает каждый узел слева направо.
Структура бинарного дерева.
Проектирование структуры бинарного дерева. Используйте характеристики односторонней связанной таблицы и сходство с двоичным деревом для проектирования.
- Дерево представляет собой рекурсивную форму, оно связано и хранится между каждым узлом.
- Бинарное дерево имеет только левое и правое поддеревья
type TreeNode struct {
Data int // Used to store data
Left *TreeNode // left subtree
Right *TreeNode // right subtree
Right *TreeNode // Right subtree
}Создание бинарного дерева.
Основная идея состоит в том, чтобы создать бинарное дерево, используя характеристики односторонней цепной таблицы (собственно, здесь ее нельзя назвать односторонней цепной таблицей, потому что это должна быть односторонняя цепная таблица; корневой узел указывает на два дочерних узла), поэтому узлы бинарного дерева являются узлами цепной таблицы.
func CreateNode(v int) *TreeNode {
return &TreeNode{v, nil, nil}
}
Добавление данных в бинарное дерево.
Основная идея состоит в том, чтобы начать только с одного корневого узла, затем по мере необходимости либо в направлении левого поддерева, либо в направлении правого поддерева, и просто связать напрямую с новым узлом, и так далее и тому подобное.
func InitTree() *TreeNode {
root := CreateNode(1) //root node
root.Left = CreateNode(2) //left subtree
root.Right = CreateNode(3) //right subtree
root.Left.Right = CreateNode(4) //right subtree of left subtree
root.Right.Left = CreateNode(5) //left subtree of the left subtree of the right subtree
root.Left.Left = CreateNode(6)
root.Right.Right = CreateNode(7)
return root
}
Схематическая диаграмма результата выглядит следующим образом:
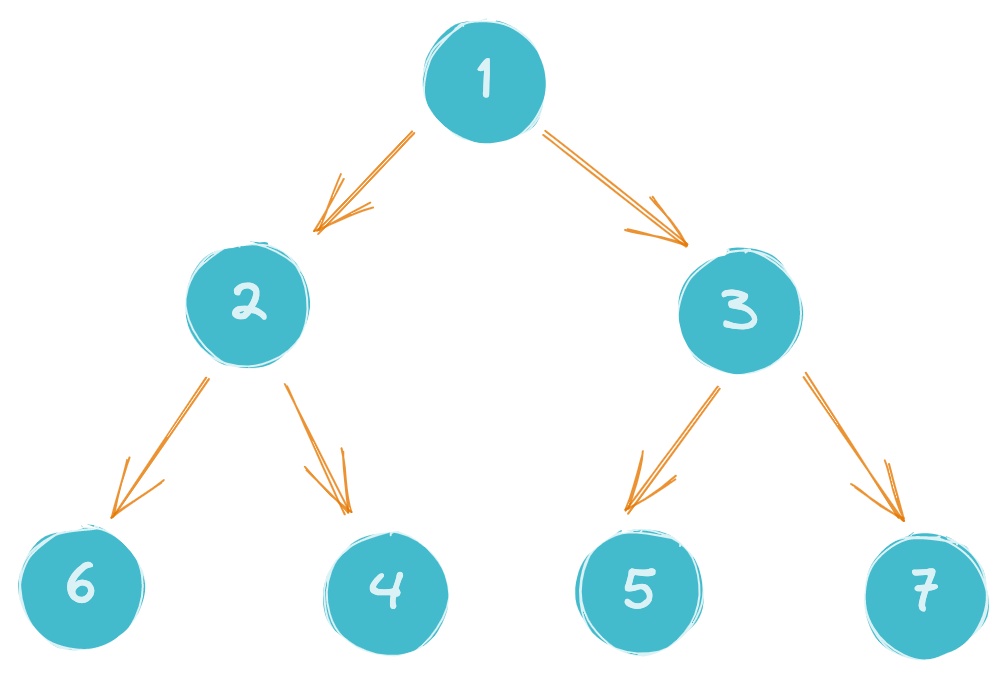
Подсчет количества узлов в бинарном дереве.
Мы используем приведенный выше пример для тестирования. Поскольку бинарное дерево является рекурсивной структурой, мы можем использовать рекурсию для обхода вычислений.
func (root *TreeNode) GetTreeNodeNum() int {
if root == nil {
return 0
} else {
// calculate the number of nodes under the left node
// calculate the number of nodes under the right node
// and finally add the number of root nodes.
return root.Left.GetTreeNodeNum() + root.Right.GetTreeNodeNum() + 1
}
}
Вычисление глубины бинарного дерева.
Глубина дерева также является максимальным уровнем дерева.
Корневой узел — это первый уровень, и пока существует левое поддерево или существует правое поддерево, уровень нужно добавить на единицу, и расчет продолжается до конца.
Таким образом, это можно сделать снова с помощью рекурсии.
func (root *TreeNode) GetTreeDegree() int {
maxDegree := 0
if root == nil {
return maxDegree
}
if root.Left.GetTreeDegree() > root.Right.GetTreeDegree() {
maxDegree = root.Left.GetTreeDegree()
} else {
maxDegree = root.Right.GetTreeDegree()
}
return maxDegree + 1
}
Обход четырех видов бинарных деревьев.
Первые три являются простыми, используя рекурсивные методы, а четвертый метод более сложен.
- Обход в прямом порядке
Для обхода бинарного дерева в прямом порядке выполняются следующие операции:
- Посетите корень.
- Обходим левое поддерево корня.
- Пройдите по правому поддереву корня.
func (root *TreeNode) PreOrder() {
if root != nil {
// print root
fmt.Print(root.Data, " ")
// print left tree
root.Left.PreOrder()
// print right tree
root.Right.PreOrder()
}
}
Для приведенного выше примера результат должен быть выведен 1 2 6 4 3 5 7.
2. Постпорядковый обход
Для обхода бинарного дерева в обратном порядке выполняются следующие операции:
- Обходим левое поддерево корня.
- Пройдите по правому поддереву корня.
- Посетите корень.
func (root *TreeNode) PostOrder() {
if root != nil {
// print left tree
root.Left.PostOrder()
// print right tree
root.Right.PostOrder()
// print root
fmt.Print(root.Data, " ")
}
}
Для приведенного выше примера результат должен быть выведен 6 4 2 5 7 3 1.
3. Неупорядоченный обход
Для обхода бинарного дерева в порядке обхода выполняются следующие операции:
- Пройдите по самому левому поддереву.
- Посетите корень.
- Пройдите по самому правому поддереву.
func (root *TreeNode) MidOrder() {
if root != nil {
// print left tree
root.Left.MidOrder()
// print root
fmt.Print(root.Data, " ")
// print right tree
root.Right.MidOrder()
}
}
Для приведенного выше примера результат должен быть выведен 6 2 4 1 5 3 7.
4. Обход порядка уровней.
Главная мысль.
Поскольку это древовидная структура и требуется выводить результаты слой за слоем, после вывода значения левого узла необходимо вывести значение правого узла этого слоя.
Предыдущие три метода соответствуют способу вывода модели «небольшое трехузловое дерево», поэтому эти три метода не могут сразу найти нужный узел по соседству.
Таким образом, мы можем рассмотреть возможность создания кэша очереди (функция «первым поступил — первым обслужен»), обхода данных и помещения их в очередь в порядке вывода.
Таким образом, решение состоит в том, чтобы реализовать каждый уровень для доступа к каждому узлу слева направо.
Во-первых, поместите корневой узел дерева в очередь, вам нужно определить очередь таблицы цепочки.
Удалите узел из очереди, сначала выведите значение узла, если узел имеет левый узел поддерева, левое поддерево отправляется в стек, если узел имеет правый узел поддерева, правое поддерево отправляется в стек.
Повторяйте до тех пор, пока в очереди не останется элементов.
func (root *TreeNode) LayerOrder() {
if root == nil {
return
}
// new a queue
queue := new(LinkQueue)
// add root
queue.Add(root)
for queue.size > 0 {
// Constantly out of queue
element := queue.Remove()
fmt.Print(element.Data, " ")
// The left subtree is not empty and is in the queue
if element.Left != nil {
queue.Add(element.Left)
}
// The right subtree is not empty and is in the queue
if element.Right != nil {
queue.Add(element.Right)
}
}
}
Полный код обхода бинарного дерева по уровням.
type LinkNode struct {
Next *LinkNode
Value *TreeNode
}
// Chained queue, first in first out
type LinkQueue struct {
root *LinkNode // Starting point of the chain table
size int // Number of elements in the queue
lock sync.Mutex // Locks used for concurrent security
}
// in
func (queue *LinkQueue) Add(v *TreeNode) {
queue.lock.Lock()
defer queue.lock.Unlock()
// If the top of the stack is empty, then add the node
if queue.root == nil {
queue.root = new(LinkNode)
queue.root.Value = v
} else {
// Otherwise the new element is inserted at the end of the chain
newNode := new(LinkNode)
newNode.Value = v
// Traverse all the way to the end of the chain
nowNode := queue.root
for nowNode.Next != nil {
nowNode = nowNode.Next
}
// The new node is placed at the end of the chain
nowNode.Next = newNode
}
// Number of elements in the queue +1
queue.size = queue.size + 1
}
//
func (queue *LinkQueue) Remove() *TreeNode {
queue.lock.Lock()
defer queue.lock.Unlock()
// empty queue
if queue.size == 0 {
panic("over limit")
}
// pop the top element
topNode := queue.root
v := topNode.Value
// Chain the top element's successor links
queue.root = topNode.Next
// Number of elements in the queue -1
queue.size = queue.size - 1
return v
}