Освоение анализа временных рядов с помощью классов Python

Анализ временных рядов - одна из наиболее распространенных задач в области науки о данных. Это включает в себя анализ тенденций в точках данных, упорядоченных во времени. Существует широкий спектр данных временных рядов, включая данные о фондовом рынке, данные о погоде, данные о потребительском спросе и многое другое. Анализ временных рядов находит применение в широком спектре отраслей, что делает его незаменимым навыком для специалистов по обработке данных и аналитиков данных.
Анализ временных рядов включает в себя множество методов, которые невозможно обобщить в одной статье. Некоторые из наиболее распространенных подходов включают визуализацию данных временных рядов с помощью линейных диаграмм, построение моделей прогнозирования временных рядов, выполнение спектрального анализа для выявления циклических тенденций, анализ тенденций сезонности и многое другое.
Поскольку анализ временных рядов включает в себя множество различных методов, он естественным образом поддается объектно-ориентированному программированию. Классы Python упрощают организацию атрибутов и методов для связанных задач временных рядов. Например, если вы, как специалист по обработке данных, часто выполняете визуализацию линейных диаграмм, анализ сезонности и прогнозирование временных рядов, классы могут позволить вам легко организовать методы и атрибуты для этих задач.
При правильном выполнении объектно-ориентированное программирование может улучшить читаемость, возможность повторного использования, ремонтопригодность и повторяемость экспериментов с временными рядами. Поскольку классы представляют собой набор методов и атрибутов, это дает понять, какие функции используются для определенной цели. Это упрощает модификацию и обслуживание существующих функций. Кроме того, как только у вас есть надежный набор методов, определенных в вашем классе, вы можете легко повторно запускать эксперименты с различными параметрами, обновленными обучающими данными и многим другим практически без необходимости переписывать код.
Здесь мы рассмотрим, как написать класс, который организует шаги в рамках рабочего процесса анализа временных рядов. Каждая часть рабочего процесса будет определена методом класса, который выполняет одну задачу. Мы рассмотрим, как определить методы класса для визуализации временных рядов, статистического тестирования, разделения данных для обучения и тестирования, обучения модели прогнозирования и проверки нашей модели временных рядов.
Для этой работы мы будем писать код в Deepnote, который представляет собой блокнот для совместной работы с данными, который очень упрощает проведение воспроизводимых экспериментов.
Для нашего моделирования мы будем работать с набором данных временных рядов фиктивной погоды и климата, который находится в открытом доступе на Kaggle. Набор данных можно свободно использовать, изменять и распространять в соответствии с лицензией Creative Commons Universal Public Domain License (CC0 1.0).
Считывание данных
Для начала давайте перейдем к Deepnote и создадим новый проект (вы можете зарегистрироваться бесплатно, если у вас еще нет учетной записи).
Давайте создадим проект под названием «time_series» и записную книжку в этом проекте под названием «time_series_oop». Кроме того, давайте перетащим файл DailyDelhiClimate.csv на левую панель страницы, где указано «FILES»:
Давайте начнем с импорта библиотеки Pandas:
import pandas as pdДалее мы определим класс, который позволит нам читать наши данные о погоде. Мы назовем наш класс Python TimeSeriesAnalysis:
class TimeSeriesAnalysis:
def __init__(self, data):
self.df = pd.read_csv(data)Мы можем определить экземпляр нашего класса и получить доступ к вашему фрейму данных через наш объект анализа временных рядов. Давайте отобразим первые пять строк наших данных:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate_df = climate.df
climate_df.head()| Month object | #Passengers int64 | |
| 0 | 1949-01 | 112 |
| 1 | 1949-02 | 118 |
| 2 | 1949-03 | 132 |
| 3 | 1949-04 | 129 |
| 4 | 1949-05 | 121 |
Мы видим, что у нас есть объект даты и четыре столбца с плавающей запятой. У нас есть средняя температура, влажность, скорость ветра и среднее давление. Давайте добавим в наш класс метод, который подготавливает временные ряды. Метод примет числовое имя столбца и вернет временной ряд, где данные — это индекс, а значения соответствуют выбранному столбцу:
class TimeSeriesAnalysis:
...
def get_time_series(self, target):
self.df['date'] = pd.to_datetime(self.df['date'])
self.df.set_index('date', inplace=True)
self.ts_df = self.df[target]Теперь мы можем определить новый экземпляр нашего класса и получить доступ к нашим данным временных рядов:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
ts_df = climate.ts_df
ts_df.head()date
2013-01-01 10.000000
2013-01-02 7.400000
2013-01-03 7.166667
2013-01-04 8.666667
2013-01-05 6.000000
Name: meantemp, dtype: float64Генерирование сводной статистики
Следующее, что мы можем сделать, это добавить метод, который генерирует некоторую базовую сводную статистику для наших временных рядов. Например, мы можем определить метод класса, который возвращает среднее значение и стандартное отклонение для указанного столбца:
class TimeSeriesAnalysis:
...
def get_summary_stats(self):
print(f"Mean {self.target}: ", self.ts_df.mean())
print(f"Standard Dev. {self.target}: ", self.ts_df.std())Затем мы можем определить новый экземпляр класса, вызвать метод get_time_series для нашего экземпляра объекта со столбцами средней температуры в качестве входных данных и сгенерировать сводную статистику:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
climate.get_summary_stats()Mean meantemp: 25.495520655761762
Standard Dev. meantemp: 7.348102725432476
Мы можем сделать то же самое для влажности, скорости ветра и среднего давления.
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('humidity')
climate.get_summary_stats()
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('wind_speed')
climate.get_summary_stats()
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meanpressure')
climate.get_summary_stats()Mean humidity: 60.77170158004638
Standard Dev. humidity: 16.769652268485306
Mean wind_speed: 6.802208747447473
Standard Dev. wind_speed: 4.561602164272007
Mean meanpressure: 1011.1045475940377
Standard Dev. meanpressure: 180.2316683392096
Визуализация временных рядов
Следующее, что мы можем сделать, - это определить метод, который позволяет нам генерировать некоторые визуализации. Для наших визуализаций нам нужно будет импортировать Seaborn, Matplotlib и пакет statsmodels:
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as smДавайте определим новый экземпляр класса для средней температуры и создадим линейный график, гистограмму и выполним сезонную декомпозицию:
class TimeSeriesAnalysis:
...
def visualize(self, line_plot, histogram, decompose):
sns.set()
if line_plot:
plt.plot(self.ts_df)
plt.title(f"Daily {self.target}")
plt.xticks(rotation=45)
plt.show()
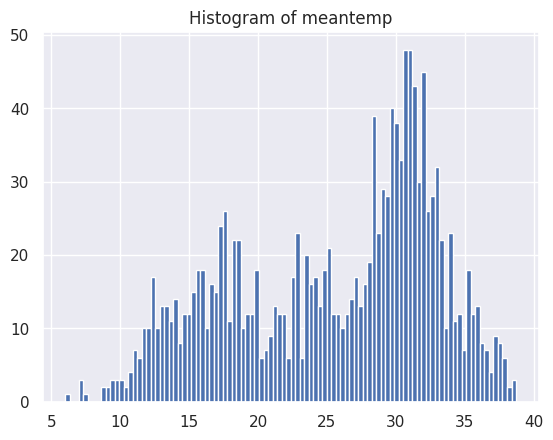
if histogram:
self.ts_df.hist(bins=100)
plt.title(f"Histogram of {self.target}")
plt.show()
if decompose:
decomposition = sm.tsa.seasonal_decompose(self.ts_df, model='additive', period =180)
fig = decomposition.plot()
plt.show()Пусть наш метод дает возможность генерировать гистограмму целевых значений, график временных рядов и декомпозицию временных рядов:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
climate.visualize(line_plot = True, histogram = True, decompose = True)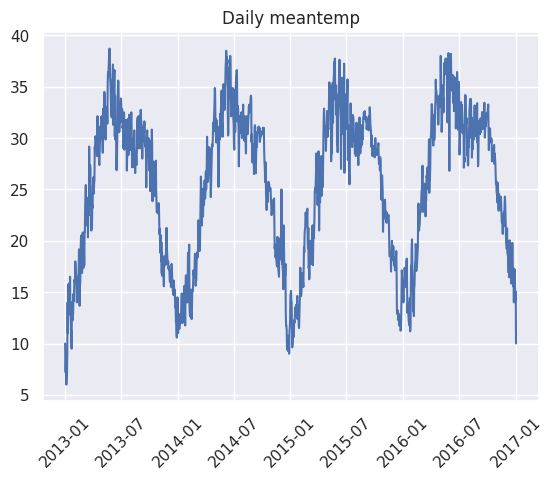
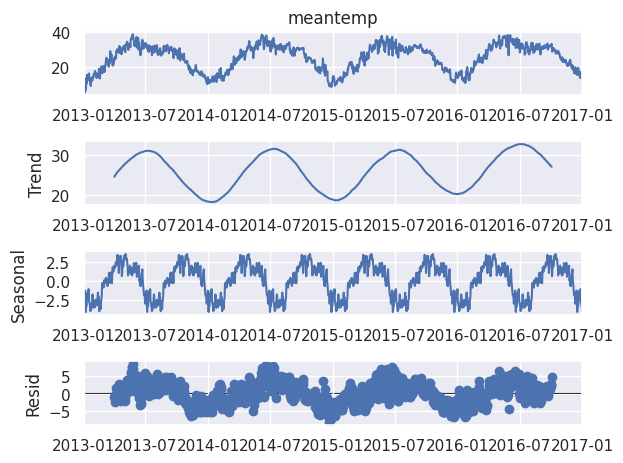
Тесты на стационарность
Adjusters Dickey-Fuller
Другой метод, который мы можем добавить, - это проверка на стационарность с использованием теста Дики-Фуллера. Стационарность - это когда среднее значение и дисперсия временного ряда не меняются с течением времени. Более того, если временной ряд является стационарным, у него нет никаких тенденций. Осмотрев наш график, мы видим, что данные о погоде нестационарны, поскольку существуют четкие сезонные тенденции. Мы будем использовать тест Дики-Фуллера для проверки стационарности. Тест Дики-Фуллера имеет следующую гипотезу:
Нулевая гипотеза: временной ряд нестационарен.
Альтернативная гипотеза: временной ряд является стационарным.
Мы интерпретируем результаты следующим образом:
Если тестовая статистика превышает критические значения, мы отвергаем нулевую гипотезу.
Если тестовая статистика превышает критические значения, нам не удалось отклонить нулевую гипотезу.
Результаты теста будут иметь критические значения на уровнях значимости 1%, 5% и 10%. Он также будет содержать статистику тестирования. Давайте определим метод, который позволяет нам запустить этот тест:
class TimeSeriesAnalysis:
...
def stationarity_test(self):
adft = adfuller(self.ts_df,autolag="AIC")
output_df = pd.DataFrame({"Values":[adft[0],adft[1],adft[2],adft[3], adft[4]['1%'], adft[4]['5%'], adft[4]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used","Number of observations used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
self.adf_results = output_dfВ верхней части нашей записной книжки давайте импортируем метод adfuller из пакетов моделей статистики:
from statsmodels.tsa.stattools import adfullerЗатем мы можем вызвать метод stationarity_test для нашего объекта climate и получить доступ к результатам тестирования:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
climate.stationarity_test()
climate.adf_results warnings.warn(| Values float64 | Metric object | |
| 0 | -2.021069055920674 | Статистика испытаний |
| 1 | 0.2774121372301599 | p-значение |
| 2 | 10.0 | Количество используемых лагов |
| 3 | 1451.0 | Количество использованных наблюдений |
| 4 | -3.4348647527922824 | критическое значение (1%) |
| 5 | -2.863533960720434 | критическое значение (5%) |
| 6 | -2.567831568508802 | критическое значение (10%) |
Мы видим, что в каждом случае критические значения меньше ожидаемой тестовой статистики. Это означает, что наши данные нестационарны.
Kwiatkowski — Phillips — Schmidt — Shin (KPSS)
Нулевая гипотеза: временной ряд является стационарным.
Альтернативная гипотеза: временной ряд не является стационарным.
Подобно тесту ADF, мы интерпретируем результаты следующим образом:
Если тестовая статистика превышает критические значения, мы отвергаем нулевую гипотезу.
Если тестовая статистика превышает критические значения, нам не удалось отклонить нулевую гипотезу.
Еще одним тестом на стационарность является тест Kwiatkowski — Phillips — Schmidt — Shin (KPSS). Нулевая гипотеза для этого теста состоит в том, что временной ряд является стационарным. Разница между ADF и KPSS заключается в том, что ADF проверяет стационарность, а KPSS проверяет нестационарность. Если в результате теста ADF не удается отклонить нулевую гипотезу, следует использовать KPSS, чтобы подтвердить нестационарность временного ряда. Давайте расширим наш метод проверки на стационарность, чтобы он давал варианты как для ADF, так и для KPSS. Давайте импортируем метод KPSS из моделей sstats:
from statsmodels.tsa.stattools import adfuller, kpssЗатем мы можем расширить определение нашего стационарного метода тестирования, включив в него KPSS:
class TimeSeriesAnalysis:
...
def stationarity_test(self):
adft = adfuller(self.ts_df,autolag="AIC")
kpsst = kpss(self.ts_df,autolag="AIC")
adf_results = pd.DataFrame({"Values":[adft[0],adft[1],adft[2],adft[3], adft[4]['1%'], adft[4]['5%'], adft[4]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used","Number of observations used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
kpss_results = pd.DataFrame({"Values":[kpsst[0],kpsst[1],kpsst[2], kpsst[3]['1%'], kpsst[3]['5%'], kpsst[3]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
self.adf_results = adf_results
self.kpss_resulta = kpss_resultsИ затем мы можем вызвать метод stationarity_test для нашего объекта climate и получить доступ к результатам теста KPSS:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
climate.stationarity_test()
climate.kpss_results/usr/local/lib/python3.9/site-packages/statsmodels/tsa/stattools.py:2022: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.
warnings.warn(| Values float64 | Metric object | |
| 0 | 0.18786352260533618 | Статистика испытаний |
| 1 | 0.1 | р-значение |
| 2 | 25.0 | Количество используемых лагов |
| 3 | 0.739 | критическое значение (1%) |
| 4 | 0.463 | критическое значение (5%) |
| 5 | 0.347 | критическое значение (10%) |
Мы видим, что тестовая статистика меньше критических значений, что означает, что мы отвергаем нулевую гипотезу. Нулевая гипотеза утверждает, что временной ряд является стационарным. Это означает, что у нас есть доказательства, подтверждающие утверждение о том, что временные ряды нестационарны.
Мы можем определить метод, который выполняет тесты ADF и KPSS и печатает результаты:
class TimeSeriesAnalysis:
...
def stationarity_test(self):
adft = adfuller(self.ts_df,autolag="AIC")
kpsst = kpss(self.ts_df)
adf_results = pd.DataFrame({"Values":[adft[0],adft[1],adft[2],adft[3], adft[4]['1%'], adft[4]['5%'], adft[4]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used","Number of observations used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
kpss_results = pd.DataFrame({"Values":[kpsst[0],kpsst[1],kpsst[2], kpsst[3]['1%'], kpsst[3]['5%'], kpsst[3]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
self.adf_results = adf_results
self.kpss_results = kpss_results
print(self.adf_results)
print(self.kpss_results)
self.adf_status = adf_results['Values'].iloc[1] > adf_results['Values'].iloc[4]
self.kpss_status = kpss_results['Values'].iloc[1] < kpss_results['Values'].iloc[3]
print("ADF Results: ", self.adf_status)
print("KPSS Results: " ,self.kpss_status) И мы получаем:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
climate.stationarity_test()
Values Metric
0 -2.021069 Test Statistics
1 0.277412 p-value
2 10.000000 No. of lags used
3 1451.000000 Number of observations used
4 -3.434865 critical value (1%)
5 -2.863534 critical value (5%)
6 -2.567832 critical value (10%)
Values Metric
0 0.187864 Test Statistics
1 0.100000 p-value
2 25.000000 No. of lags used
3 0.739000 critical value (1%)
4 0.463000 critical value (5%)
5 0.347000 critical value (10%)
ADF Results: True
KPSS Results: True
/usr/local/lib/python3.9/site-packages/statsmodels/tsa/stattools.py:2022: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.
warnings.warn(Лучше всего использовать оба теста, чтобы подтвердить, является ли временной ряд стационарным. Результаты обоих тестов убедительно свидетельствуют о том, что временной ряд нестационарен.
Интересно, что наиболее распространенные методы прогнозирования временных рядов, такие как ARIMA и SARIMA, могут обрабатывать нестационарные данные. Как правило, в моделях ARIMA рекомендуется выполнить дифференцирование перед установкой вашей модели. Auto ARIMA - это пакет python, который позволяет вам автоматически искать наилучший параметр различия. Это удобно, поскольку нет необходимости выполнять ручной тест, чтобы найти наилучший порядок разности.
Сплит для обучения и тестирования
При подготовке данных для обучающих моделей прогнозирования важно разделить данные для обучения и тестирования. Это помогает предотвратить перенастройку модели данными и, следовательно, плохое обобщение. Мы определим обучение как все данные до июля 2016 года, а тестирование как все точки данных после июля 2016 года:
def train_test_split(self):
self.y_train = self.ts_df[self.ts_df.index <= pd.to_datetime('2016-07')]
self.y_test = self.ts_df[self.ts_df.index > pd.to_datetime('2016-07')]Модель Auto ARIMA
Чтобы использовать Auto ARIMA, сначала установите пакет pdarima:
!pip install pmdarimaДалее импортируем auto arima из pmdarima:
from pmdarima.arima import auto_arimaЗатем мы можем определить наш метод подгонки, который мы будем использовать для подгонки нашей модели ARIMA к нашим обучающим данным:
def fit(self):
self.y_train.fillna(0,inplace=True)
model = auto_arima(self.y_train, trace=True, error_action='ignore', suppress_warnings=True, stationary=True)
model.fit(self.y_train)
forecast = model.predict(n_periods=len(self.ts_df))
self.forecast = pd.DataFrame(forecast,index = self.ts_df.index,columns=['Prediction'])
self.ts_df = pd.DataFrame(self.ts_df, index = self.forecast.index)
self.y_train = self.ts_df[self.ts_df.index < pd.to_datetime('2016-07')]
self.y_test = self.ts_df[self.ts_df.index > pd.to_datetime('2016-07')]
self.forecast = self.forecast[self.forecast.index > pd.to_datetime('2016-07')]Мы также определим метод проверки, который отображает производительность и визуализирует прогнозы модели. Мы будем использовать среднюю абсолютную ошибку для оценки производительности:
def validate(self):
plt.plot(self.y_train, label='Train')
plt.plot(self.y_test, label='Test')
plt.plot(self.forecast, label='Prediction')
mae = np.round(mean_absolute_error(self.y_test, self.forecast), 2)
plt.title(f'{self.target} Prediction; MAE: {mae}')
plt.xlabel('Date')
plt.ylabel(f'{self.target}')
plt.xticks(rotation=45)
plt.legend(loc='upper left', fontsize=8)
plt.show()Полный класс выглядит следующим образом:
class TimeSeriesAnalysis:
def __init__(self, data):
self.df = pd.read_csv(data)
def get_time_series(self, target):
self.target = target
self.df['date'] = pd.to_datetime(self.df['date'])
self.df.set_index('date', inplace=True)
self.ts_df = self.df[target]
def get_summary_stats(self):
print(f"Mean {self.target}: ", self.ts_df.mean())
print(f"Standard Dev. {self.target}: ", self.ts_df.std())
def visualize(self, line_plot, histogram, decompose):
sns.set()
if line_plot:
plt.plot(self.ts_df)
plt.title(f"Daily {self.target}")
plt.xticks(rotation=45)
plt.show()
if histogram:
self.ts_df.hist(bins=100)
plt.title(f"Histogram of {self.target}")
plt.show()
if decompose:
decomposition = sm.tsa.seasonal_decompose(self.ts_df, model='additive', period =180)
fig = decomposition.plot()
plt.show()
def stationarity_test(self):
adft = adfuller(self.ts_df,autolag="AIC")
kpsst = kpss(self.ts_df)
adf_results = pd.DataFrame({"Values":[adft[0],adft[1],adft[2],adft[3], adft[4]['1%'], adft[4]['5%'], adft[4]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used","Number of observations used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
kpss_results = pd.DataFrame({"Values":[kpsst[0],kpsst[1],kpsst[2], kpsst[3]['1%'], kpsst[3]['5%'], kpsst[3]['10%']] , "Metric":["Test Statistics","p-value","No. of lags used",
"critical value (1%)", "critical value (5%)", "critical value (10%)"]})
self.adf_results = adf_results
self.kpss_results = kpss_results
print(self.adf_results)
print(self.kpss_results)
self.adf_status = adf_results['Values'].iloc[1] > adf_results['Values'].iloc[4]
self.kpss_status = kpss_results['Values'].iloc[1] < kpss_results['Values'].iloc[3]
print("ADF Results: ", self.adf_status)
print("KPSS Results: ", self.kpss_status)
def train_test_split(self):
self.y_train = self.ts_df[self.ts_df.index <= pd.to_datetime('2016-07')]
def fit(self):
self.y_train.fillna(0,inplace=True)
model = auto_arima(self.y_train, trace=True, error_action='ignore', suppress_warnings=True, stationary=True)
model.fit(self.y_train)
forecast = model.predict(n_periods=len(self.ts_df))
self.forecast = pd.DataFrame(forecast,index = self.ts_df.index,columns=['Prediction'])
self.ts_df = pd.DataFrame(self.ts_df, index = self.forecast.index)
self.y_train = self.ts_df[self.ts_df.index < pd.to_datetime('2016-07')]
self.y_test = self.ts_df[self.ts_df.index > pd.to_datetime('2016-07')]
self.forecast = self.forecast[self.forecast.index > pd.to_datetime('2016-07')]
def validate(self):
plt.plot(self.y_train, label='Train')
plt.plot(self.y_test, label='Test')
plt.plot(self.forecast, label='Prediction')
mae = np.round(mean_absolute_error(self.y_test, self.forecast), 2)
plt.title(f'{self.target} Prediction; MAE: {mae}')
plt.xlabel('Date')
plt.ylabel(f'{self.target}')
plt.xticks(rotation=45)
plt.legend(loc='upper left', fontsize=8)
plt.show()Теперь, если мы определим новый экземпляр, поместим и проверим нашу модель, мы получим:
climate = TimeSeriesAnalysis('DailyDelhiClimate.csv')
climate.get_time_series('meantemp')
climate.stationarity_test()
climate.train_test_split()
climate.fit()
climate.validate()/usr/local/lib/python3.9/site-packages/statsmodels/tsa/stattools.py:2022: InterpolationWarning: The test statistic is outside of the range of p-values available in the
look-up table. The actual p-value is greater than the p-value returned.
warnings.warn(
Values Metric
0 -2.021069 Test Statistics
1 0.277412 p-value
2 10.000000 No. of lags used
3 1451.000000 Number of observations used
4 -3.434865 critical value (1%)
5 -2.863534 critical value (5%)
6 -2.567832 critical value (10%)
Values Metric
0 0.187864 Test Statistics
1 0.100000 p-value
2 25.000000 No. of lags used
3 0.739000 critical value (1%)
4 0.463000 critical value (5%)
5 0.347000 critical value (10%)
ADF Results: True
KPSS Results: True
Performing stepwise search to minimize aic
ARIMA(2,0,2)(0,0,0)[0] intercept : AIC=4889.074, Time=0.67 sec
ARIMA(0,0,0)(0,0,0)[0] intercept : AIC=8794.714, Time=0.02 sec
ARIMA(1,0,0)(0,0,0)[0] intercept : AIC=4964.979, Time=0.09 sec
ARIMA(0,0,1)(0,0,0)[0] intercept : AIC=7460.381, Time=0.09 sec
ARIMA(0,0,0)(0,0,0)[0] : AIC=11992.795, Time=0.01 sec
ARIMA(1,0,2)(0,0,0)[0] intercept : AIC=4909.653, Time=0.20 sec
ARIMA(2,0,1)(0,0,0)[0] intercept : AIC=4887.780, Time=0.29 sec
ARIMA(1,0,1)(0,0,0)[0] intercept : AIC=4933.446, Time=0.13 sec
ARIMA(2,0,0)(0,0,0)[0] intercept : AIC=4941.625, Time=0.11 sec
ARIMA(3,0,1)(0,0,0)[0] intercept : AIC=4888.926, Time=0.55 sec
ARIMA(3,0,0)(0,0,0)[0] intercept : AIC=4930.146, Time=0.17 sec
ARIMA(3,0,2)(0,0,0)[0] intercept : AIC=4890.438, Time=0.59 sec
ARIMA(2,0,1)(0,0,0)[0] : AIC=4892.312, Time=0.06 sec
Best model: ARIMA(2,0,1)(0,0,0)[0] intercept
Total fit time: 2.987 seconds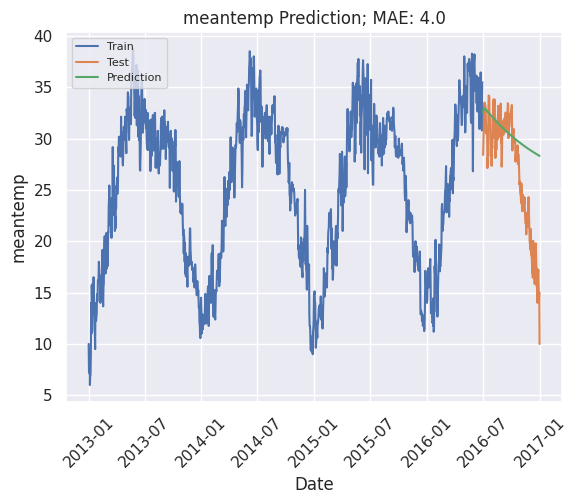
Код в этом посте доступен на GitHub.
ВЫВОДЫ
В этом посте мы обсудили, как написать класс, который организует этапы рабочего процесса анализа временных рядов. Во-первых, мы определили метод, который позволил нам считывать и отображать данные. Затем мы определили метод для вычисления среднего значения и стандартного отклонения для временных рядов. Далее мы определили метод, который позволил нам визуализировать линейные графики данных временных рядов, гистограммы значений временных рядов и сезонную декомпозицию данных. После мы написали метод класса, который позволил нам выполнять статистические тесты на стационарность. Мы использовали тест ADF для проверки на стационарность и тест KPSS для проверки на нестационарность. Наконец, мы применили модель Auto ARIMA к данным обучения, проверили нашу модель и сгенерировали визуализации для наших прогнозов. Призываем вас попробовать применить эти методы к вашим проектам анализа временных рядов!