Переосмысление анализа Survival: Как заставить вашу модель выдавать кривые Survival

В компаниях, управляемых данными, приложения для определения времени до события играют решающую роль в принятии решений (и даже больше, чем мы можем себе представить). Под анализом времени до события мы имеем в виду все методы, используемые для измерения времени, которое проходит до тех пор, пока не произойдут интересующие нас события. Это простое определение может сразу же обозначить все преимущества разработки приложений для работы с событиями времени в бизнес-контексте (и не только).
Происхождение времени до события связано с областью медицины, чтобы ответить на такие вопросы, как: «Как долго живут анализируемые лица?». По этой причине термины «выживаемость» и «время до события» обычно используются как синонимы. В настоящее время, с широкомасштабным внедрением машинного обучения, методологии выживания обычно находят применение и в компаниях, не относящихся к медицинскому/клиническому сектору. Производитель может быть заинтересован в оценке ожидаемого срока службы некоторых двигателей; поставщику услуг может потребоваться рассчитать ожидаемый срок службы своих клиентов; финансовое учреждение может оценить риск неплатежеспособности заемщика с течением времени.
С практической точки зрения, для моделирования проблемы времени до события существует надлежащий набор методологий. Было выпущено множество сред выживания, от классических линейных статистических методов до более сложных подходов к машинному обучению и передовых решений для глубокого обучения. Все они замечательны, но они должны учитывать допущение, свойственное теории моделирования выживания, что может привести к низкой адаптивности или ограничениям для реальных случаев использования. По этим причинам удобный способ заниматься анализом выживаемости может состоять в том, чтобы рассматривать моделирование времени до события как проблему классификации.
В этом посте мы предлагаем обобщение для проведения анализа выживания с прогностическими возможностями. Мы стремимся смоделировать время, прошедшее между временем начала и интересующим событием, как проблему множественной бинарной классификации. При правильной и простой постобработке мы можем получить надежные и надежные индивидуальные кривые выживания. Мы можем сделать это, используя наш любимый алгоритм классификации, сделав поиск по параметрам, как всегда, и учитывая возможность калибровки наших результатов, чтобы сделать их более надежными.
ДАННЫЕ
Организация данных, находящихся в нашем распоряжении, для реализации приложения прогнозирования выживания проста и не требует особых усилий. У нас должны быть некоторые входные функции (числовые или категориальные) и необработанная цель, как в стандартной табличной задаче регрессии/классификации. В этом контексте цель представляет собой время, прошедшее от начала мониторинга до возникновения события.
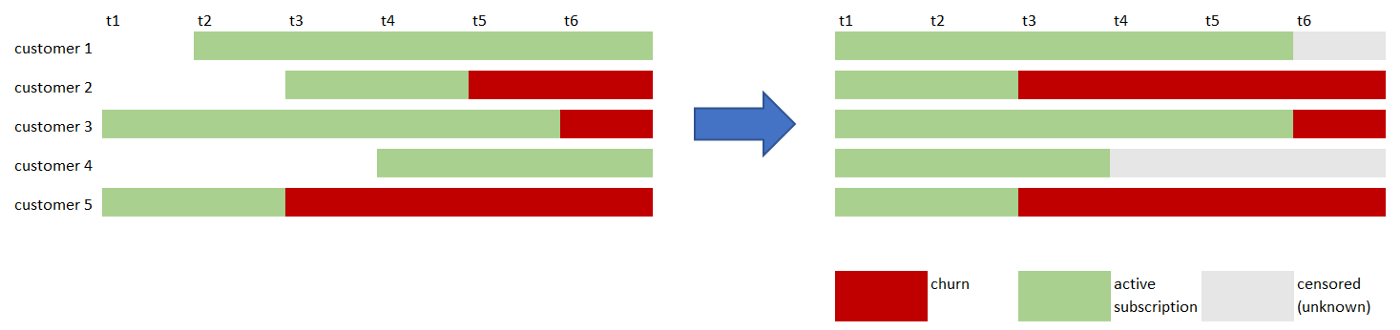
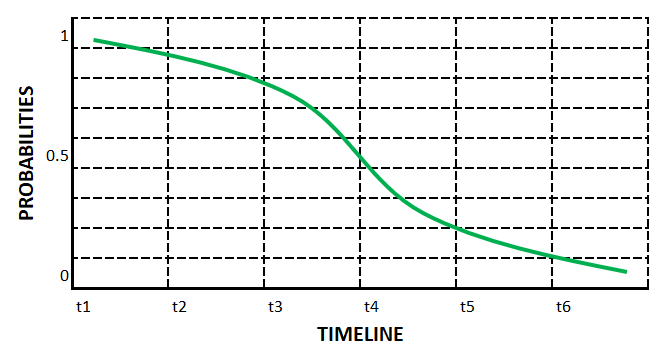
Давайте представим себя компанией, которая предлагает услугу онлайн-подписки. Мы можем быть заинтересованы в расчете ожидаемого срока службы наших клиентов на момент подписки. Другими словами, когда новый клиент попадает на нашу платформу и подписывается на получение услуг, мы хотели бы знать, как долго он/она будет оставаться нашим клиентом. Мы можем выполнить эту задачу, разработав подход к выживанию, который выводит кривые вероятности выживания (по одной для каждого клиента). Кривые выживания представляют собой последовательности монотонных вероятностей. Для каждого временного шага у нас есть числа от 0 до 1, которые указывают вероятность выживания некоторых событий (в нашем случае подписок) в этом конкретном временном диапазоне.
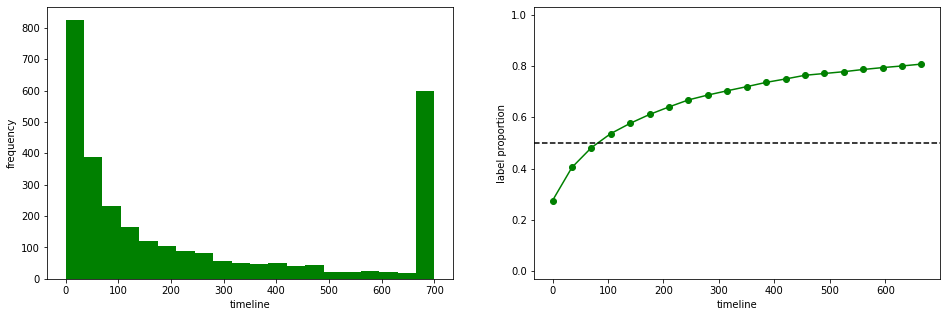
Мы моделируем некоторые функции числового ввода и цель, показывающую, сколько времени люди остаются нашими клиентами с момента их первой подписки. Из нашего моделирования мы видим, что большинство наших клиентов уходят на первом этапе после их взаимодействия (левая часть гистограммы ниже). Это представляет собой надежную динамику для большинства компаний, где через некоторое время уходит много клиентов. Наоборот, у нас есть группа лояльных подписчиков, которые остаются пользователями наших услуг (правая часть гистограммы ниже). В нашем случае мы ограничиваем максимальное наблюдаемое время подписки до 700 периодов (скажем, дней). Это предположение является обязательным, чтобы наш подход работал.
МОДЕЛИРОВАНИЕ
Начинаем разбивать время ухода на группы одинаковой длины (бины). Для каждого анализируемого клиента мы получаем нормализованную категориальную цель с несколькими уникальными классами, равными количеству созданных бинов. На этом этапе мы можем преобразовать цель с помощью горячего кодирования, в результате чего получится многомерная двоичная цель из нулей и единиц. Одни определяют, в каком временном диапазоне уходят наши клиенты (оставляют корзины). В качестве последнего шага мы должны заменить в целевых последовательностях нули на единицы слева перед «выходными ячейками». Этот последний шаг важен для обеспечения временного пути к цели, готовой к моделированию, где нули определяют временные диапазоны, в которых остаются наши клиенты.
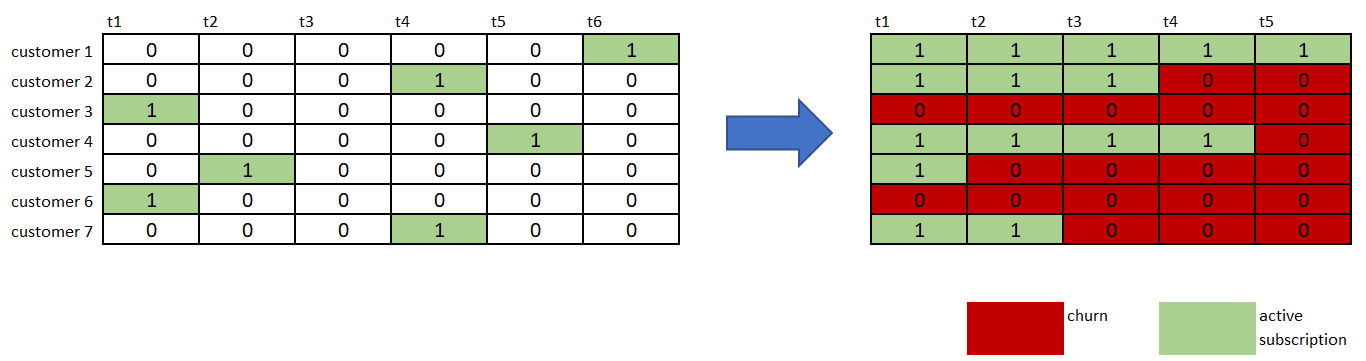
Теперь у нас есть все, что нам нужно, в правильном формате. У нас есть набор функций и многомерная бинарная цель. Другими словами, нам просто нужно решить задачу многомерной бинарной классификации. Возможность ее решения заключается в использовании нативных методологий scikit-learn (ClassifierChain).
from sklearn.multioutput import ClassifierChain
from sklearn.linear_model import LogisticRegression
model = ClassifierChain(
LogisticRegression(random_state=33, max_iter=2000), cv=5
)
model.fit(X_train, y_train)С помощью цепочки классификаторов мы моделируем нашу цель классификации с несколькими выходами как автономные, но зависимые задачи бинарной классификации. Мы говорим зависимые, поскольку выходные данные предыдущего шага объединяются с начальными функциями и используются в качестве входных данных для следующего обучения в цепочке.
После этапа обучения мы заканчиваем набором зависимых бинарных классификаторов. Каждый из них обеспечивает вероятность результата, который является частью построения окончательных индивидуальных кривых выживания. Вероятности наверняка находятся между 0 и 1, но нет никаких гарантий относительно ограничения монотонности, собственно функций выживания. Другими словами, вероятность выживания в первом временном интервале должна быть выше, чем вероятность выживания в следующих временных диапазонах. Чтобы удовлетворить это требование, мы выполняем постобработку вероятностей, полученных нашей цепочкой классификаторов на клиентских уровнях.
from sklearn.isotonic import IsotonicRegression
from joblib import Parallel, delayed
isoreg = IsotonicRegression(y_min=0, y_max=1, increasing=True)
x = np.arange(0, n_bins)
proba = model.predict_proba(X_test)
proba = Parallel(n_jobs=-1, verbose=1)(
delayed(isoreg.fit_transform)(x, p)
for p in proba
)
proba = 1 - np.asarray(proba)Просто применяя изотонические регрессии к окончательным вероятностям, мы получаем монотонные кривые выживания в качестве окончательных результатов.
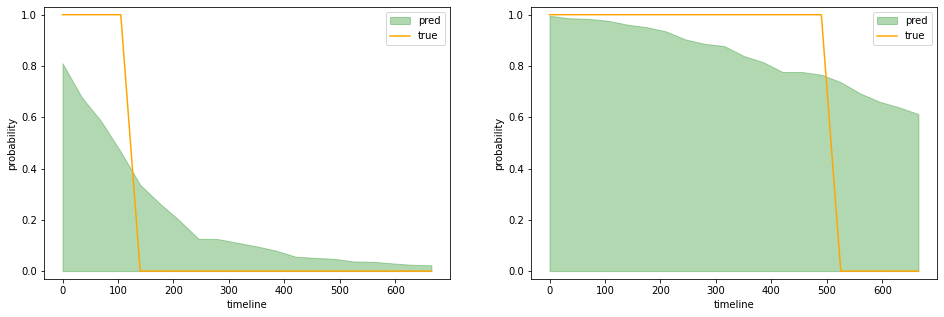
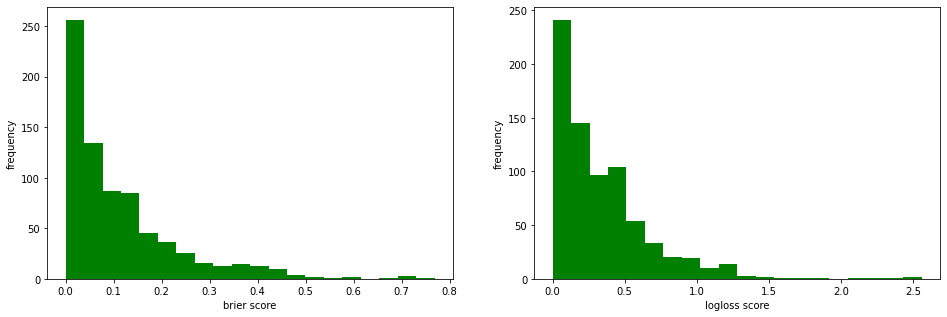
В конце концов, мы можем измерить ошибки, как и в стандартных контролируемых задачах, используя интересующие нас метрики. Мы можем использовать, например, показатель Брайера или более стандартные логистические потери.
from sklearn.metrics import brier_score_loss, log_loss
brier_scores = Parallel(n_jobs=-1, verbose=1)(
delayed(brier_score_loss)(true, pred, pos_label=1)
for true,pred in zip(y_test,proba)
)
logloss_scores = Parallel(n_jobs=-1, verbose=1)(
delayed(log_loss)(true, pred, labels=[0,1])
for true,pred in zip(y_test,proba)
)
РЕЗЮМЕ
Мы представили простой и эффективный метод создания кривых выживания с помощью стандартных классификаторов машинного обучения по нашему выбору. Мы обнаружили, что можем прогнозировать кривые выживания, моделируя наблюдаемое время отказа как последовательность бинарных целей. С помощью простой вероятностной постобработки мы получили надежные вероятностные результаты. Предлагаемую методологию можно легко обобщить и применять во многих контекстах (также с учетом цензурированных наблюдений, если их добавление целесообразно для повышения производительности).