03.05.2023 в 13:33

Прогнозируйте пределы производительности человека с помощью Python

Моделирование экспоненциального распада с помощью SciPy

Сможет ли человек когда-нибудь обогнать Ferrari? Конечно нет. Работоспособность человека изначально ограничена, и многие факторы ограничивают нашу скорость, в том числе то, насколько быстро ваша кровь может доставлять кислород и как быстро наши мышцы могут сокращаться. Если мы не подвергнемся серьезной генной инженерии, мы будем примерно такими же быстрыми, какими когда-либо будем.

Итак, откуда мы это знаем? Что ж, производительность человека, как и многие другие характеристики, соответствует распределению по колоколообразной кривой [1]. Это означает, что большинство людей находятся в пределах среднего диапазона, вблизи пика кривой, и лишь небольшой процент является исключительно медленным или быстрым. По мере того как мы удаляемся от пика, число людей с таким уровнем производительности уменьшается в геометрической прогрессии. В случае спринта это означает, что самые быстрые спринтеры уже достигли сглаженной, сужающейся части кривой. В результате добиться значительного повышения скорости будет становиться все труднее.

График пробного времени на 100 м менее 9,93 секунды, зарегистрированный с 2005 года [2]. (после инженерной школы Маккормика (2016))

Это не значит, что здесь нет возможностей для улучшения. Тренировки, питание, оборудование и другие факторы могут помочь людям улучшить свои показатели в пределах их генетических ограничений. Однако важно признать, что мы не можем коренным образом изменить наши физические ограничения, особенно если регулирующие органы продолжают ограничивать использование передовых биотехнологий в легкой атлетике.

Поскольку производительность человека ограничена, мы можем прогнозировать будущие результаты во многих видах спорта [3]. Например, сокращение времени установления мирового рекорда в беге на 100 м, как и многие другие природные явления, по-видимому, происходит по схеме экспоненциального спада [4]. В результате мы можем смоделировать это с помощью экспоненциального уравнения:

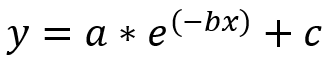
Показательное уравнение (изображение источника)

В этом уравнении y представляет прогноз времени мирового рекорда в спринте в секундах; x представляет собой количество лет, прошедших с момента установления первого рекорда; а a, b и c представляют параметры аппроксимации кривой:

a — масштабный коэффициент или амплитуда. Он определяет вертикальное растяжение или сжатие экспоненциальной функции.
b - постоянная затухания. Он показывает, как быстро функция затухает при увеличении x.
c - величина вертикального смещения. Он определяет значение y горизонтальной асимптоты, которая представляет собой горизонтальную линию, к которой экспоненциальная функция приближается, когда x приближается к бесконечности.

Эти три параметра решаются путем подгонки экспоненциальной функции к набору точек данных с использованием алгоритма подгонки кривой. Значения, которые лучше всего соответствуют данным, определяются путем минимизации суммы квадратов разностей между предсказанными значениями y и фактическими значениями y при каждом значении x.

Конечно, если вы не математик, найти правильные параметры может быть немного сложно. К счастью для всех нас, есть библиотека Python, которая упрощает оптимизацию кривых.

Библиотека SciPy

Библиотека SciPy с открытым исходным кодом расширяет возможности NumPy, предоставляя физические константы, коэффициенты преобразования и числовые процедуры для использования в математике, науке и технике [5]. К ним относятся процедуры оптимизации для подгонки кривых, что как раз то, что нам нужно для этого проекта.

Чтобы установить SciPy с использованием conda:

conda install scipy

Для установки с использованием pip:

pip install scipy

Код

Код Python для этого проекта был написан в JupyterLab. Если вы хотите скачать записную книжку, вы можете найти ее в Gist.

Импорт библиотек и настройка параметров RC

Следующая ячейка импортирует библиотеки и устанавливает параметры конфигурации запуска для фигур matplotlib. Предварительная настройка этих параметров не является строго необходимой, но сокращает количество кода позже при построении нескольких фигур.

import warnings
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.optimize

# Suppress warnings for using np.exp() on large values during optimization:
warnings.filterwarnings('ignore')

# Set default run configuration for plots:
plt.rcParams['figure.figsize'] = (6, 4)
plt.rc('font', size=12)
plt.rc('axes', titlesize=14) 
plt.rc('axes', labelsize=12) 
plt.rc('xtick', labelsize=11) 
plt.rc('ytick', labelsize=11) 
plt.rc('legend', fontsize=11)

Загрузка данных

Мировые рекорды бьются не так часто, поэтому их осталось меньше двух десятков. Воспользуемся списком рекордов на спортивном сайте topend и введем его как словарь [6]. Затем мы превратим словарь в DataFrame pandas для простоты использования. Большая часть нашего анализа будет использовать записи (в секундах) по сравнению с количеством лет, прошедших с момента первой записи, поэтому мы добавим столбец для количества лет.

# Input men's 100 m world records in seconds.
# If two records were set in the same year, list only the latest (lowest):
records = {2009: 9.58, 2008: 9.69, 2007: 9.74, 2005: 9.77, 2002: 9.78,
           1999: 9.79, 1996: 9.84, 1994: 9.85, 1991: 9.86, 1988: 9.92, 
           1983: 9.93, 1968: 9.95, 1960: 10, 1956: 10.1, 1936: 10.2, 
           1930: 10.3, 1921: 10.4, 1912: 10.6} 

# Turn dictionary into a DataFrame:
df = pd.DataFrame(records.items(), columns=['year', 'time'])
df['years'] = df['year'] - 1912  # Years since first record.
df = df.sort_values('year').reset_index(drop=True)
display(df)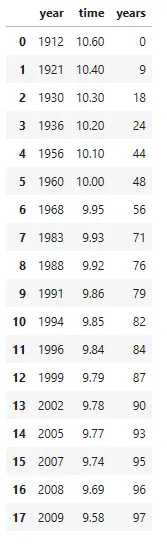

Рекорды мира на 100 м среди мужчин DataFrame (изображение источника)

Графики мировых рекордов

Всегда полезно просмотреть свои данные как можно скорее, поэтому давайте создадим базовый график из DataFrame. Это должно упростить просмотр трендов и выбросов в данных.

# Graph the world records:
plt.stem(df.year, df.time)
plt.title("Men's 100 m Sprint World Records")
plt.ylabel("Time (secs)")
plt.ylim(9.5, 10.8)
plt.grid(True);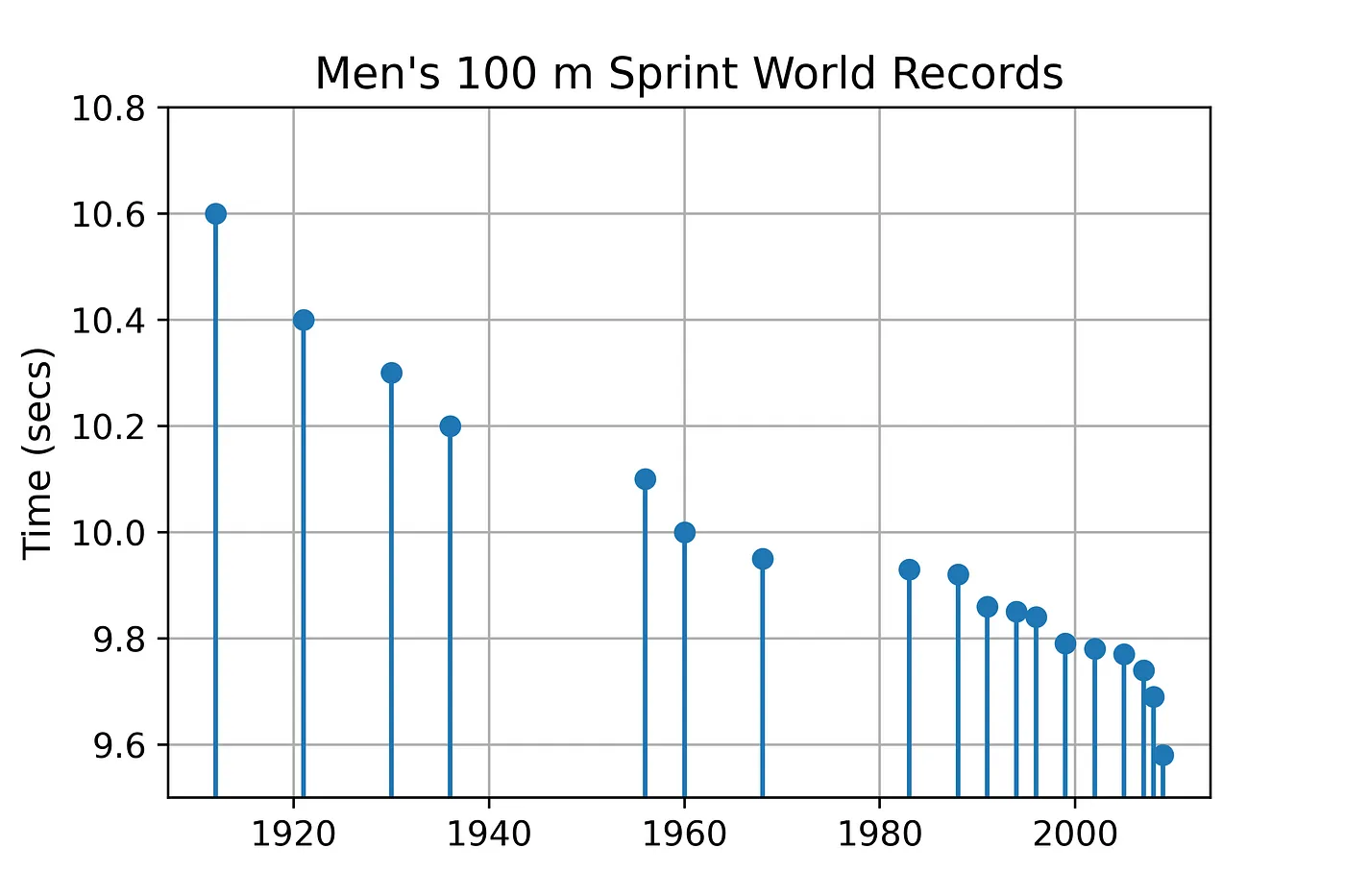

График мировых рекордов мужчин на 100 м по годам (изображение источника)

Как и следовало ожидать при экспоненциальном спаде, время записи сначала уменьшается довольно быстро, но затем начинает выравниваться, подобно самолету, приближающемуся к взлетно-посадочной полосе. В то время как современные спортсмены являются профессионалами с оптимизированными тренировками, питанием и снаряжением, добиться успеха становится все труднее по мере приближения к пределу человеческих возможностей. Или они это делают?

Посмотрите на последние две точки данных справа. Они выглядят так, словно упали со скалы. Это не плавный изгиб для мягкой посадки. Это странно. Это Усэйн Болт.

Монтаж ямайского бегуна от DALL-E2 (подсказка: драматическая картина маслом ямайского олимпийского бегуна в желтой рубашке и зеленых шортах, прорывающегося через финишную ленту, изображенного как взрыв туманности)

Безумная история Усэйна Болта

Усэйн Болт — ямайский бегун и обладатель титула «самый быстрый человек в мире» [6][7]. В 2008 году он выиграл олимпийскую золотую медаль в беге на 100 м среди мужчин со временем 9,69 секунды. Это установило новый мировой рекорд, несмотря на то, что он замедлился, чтобы отпраздновать это рано (вы можете посмотреть это здесь).

Год спустя Болт оставался сосредоточенным и пересек финишную черту со временем 9,58 секунды и максимальной скоростью 44,72 км/ч (27,79 миль в час). Этот рекорд был на несколько десятилетий раньше, чем ожидали биостатистики, основанные на математических моделях того времени.

Сегодня, благодаря Болту, прогнозы на лучшее время в беге на 100 м даются с большой скромностью и неопределенностью. Среди приведенных чисел есть относительно высокие 9,44 секунды и очень низкие 9,27 [8][9].

Чтобы оценить влияние Болта на прогнозы в беге на 100 м, давайте сделаем некоторые из них. Они будут чисто математическими и основываться только на предыдущих мировых рекордах, а не на результатах всех профессиональных гонок. Сначала мы спрогнозируем результаты без Bolt, а затем повторим процесс с Bolt. Поскольку мы будем делать это несколько раз, мы начнем с написания функций для создания и оптимизации экспоненциальных функций.

Определение функций для экспоненциального затухания

Первая функция будет принимать значения x (годы с момента первой записи) и параметры подбора кривой a, b и c и возвращать прогнозируемые значения y (время). Вторая функция будет принимать первую функцию в качестве аргумента вместе с данными x и y и использовать метод SciPy optimize.curve_fit() для автоматического выбора наиболее подходящих параметров. Мы установим для параметра p0 значение None, что означает, что мы позволим методу выбирать наилучшие минимальные и максимальные значения для предсказанных значений y, а не давать предположения.

def expo(x, a, b, c):
    """Return y values for exponential decay curve."""
    return a * np.exp(-b * x) + c

def optimize_curve_fit(a_func, x, y):
    """Return optimized parameters for curve fit."""
    params, covar = scipy.optimize.curve_fit(a_func, x, y, p0=None)
    return params

Оптимизация параметров подбора кривой

Прежде чем вызывать наши функции, нам нужно построить наборы данных мировых рекордов с временем Болта (суффикс _all) и без него (суффикс _nB). Мы передадим их вместе с нашей функцией expo() в функцию optimize_curve_fit(). Эта функция возвращает оптимизированные параметры подгонки a, b и c в виде массива NumPy.

# Generate datasets with and without Bolt's times (nB = No Bolt):
x_all, y_all = df.years, df.time
x_nB, y_nB = x_all[:-2], y_all[:-2]

# Find optimized parameters for fitting the curve to the points:
params_nB = optimize_curve_fit(expo, x_nB, y_nB)
params_all = optimize_curve_fit(expo, x_all, y_all)
print(f"Parameters without Bolt (a, b, c) = {params_nB}") 
print(f"   Parameters with Bolt (a, b, c) = {params_all}")

Parameters without Bolt (a, b, c) = [0.98795896 0.01631187 9.57391395]
   Parameters with Bolt (a, b, c) = [1.34836526 0.00941746 9.18654695]

График результатов

Чтобы построить наши прогностические кривые, мы передадим нашу функцию экспоненциального затухания (expo()) в метод matplotlib plot() вместе с оптимизированными параметрами подгонки.

# Plot exponential curves for data with and without Bolt's times:
plt.plot(x_all, y_all, '.', label='measured data', c='k')
plt.plot(x_nB, expo(x_nB, *params_nB), 
         '-', label='fitted without Bolt')
plt.plot(x_all, expo(x_all, *params_all), '--', 
         label='fitted with Bolt', c='red')
plt.title("Men's 100 m World Record")
plt.xlabel('Years Since First Record (1912)')
plt.ylabel('Times (s)')
plt.grid(True)
plt.legend(framealpha=1);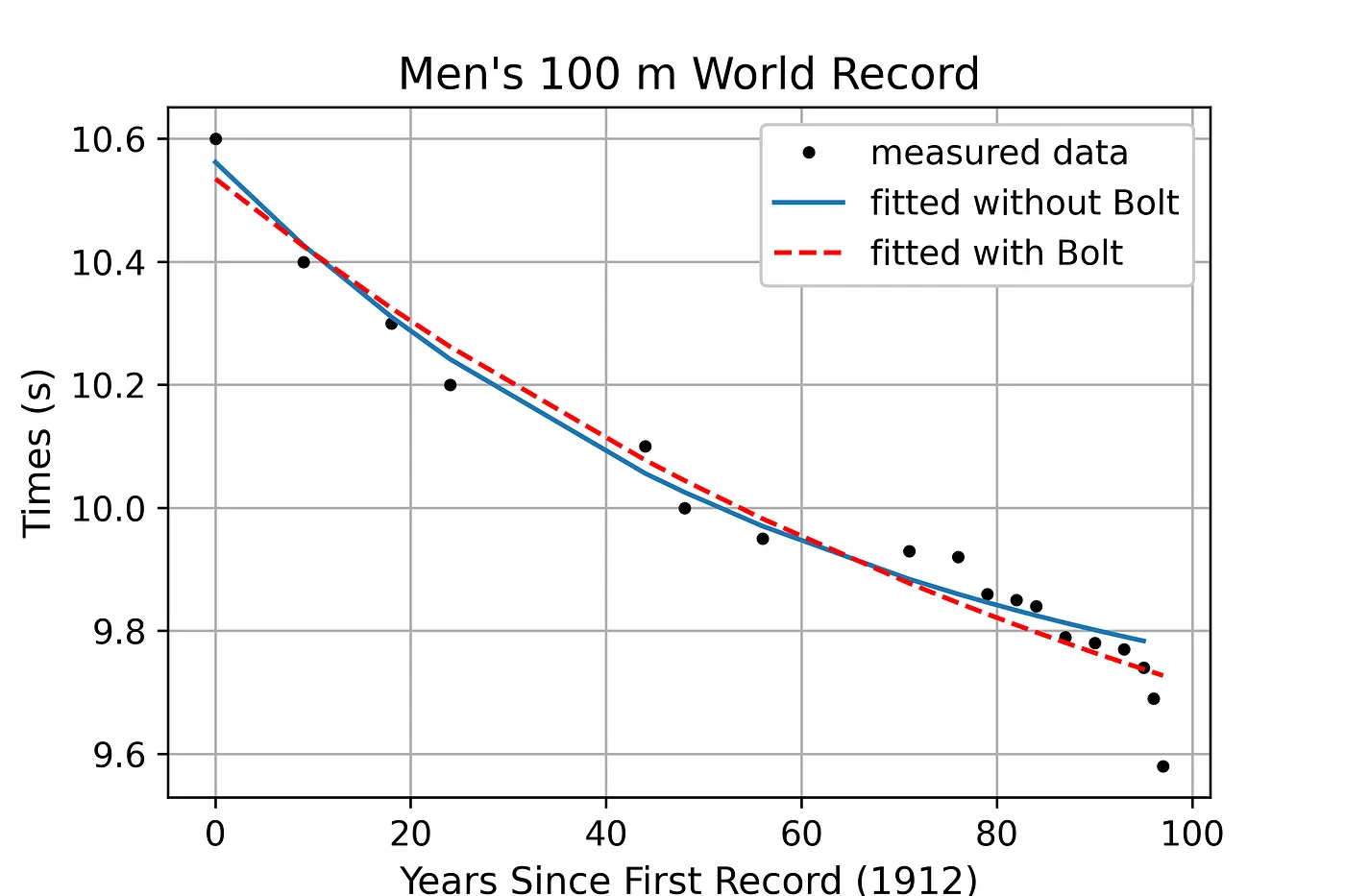

Две экспоненциальные кривые соответствуют данным мировых рекордов (изображение источника)

Усэйн Болт действительно не в себе. Это потому, что физически он изгой. Несмотря на то, что он выше, чем большинство спринтеров, и у него более длинный шаг, он все же может поддерживать аналогичную частоту шагов, что означает, что он может преодолевать то же расстояние за меньшее количество шагов. Это может быть связано с тем, что он сочетает в себе быстросокращающиеся мышечные волокна более мелких спринтеров с механическими преимуществами тела более высокого человека [8].

Здесь уместно задать вопрос, сломал ли он кривую или просто ускорил наше продвижение по ней. Для исследования нам нужно экстраполировать две кривые в будущее.

Прогнозирование будущей производительности

Следующий код сначала экстраполирует экспоненциальные кривые на 570 лет (от 20 лет до первой записи в 1912 году до 550 лет после). После построения кривых он помечает точки данных Bolt, чтобы мы могли видеть, где они пересекаются с кривыми в будущем. Наконец, он печатает минимальное время, предсказанное для каждой кривой. Обратите внимание, что эти значения совпадают с параметром c из упражнения по подгонке кривой.

# Extrapolate exponential curves to predict future performance:
x_extrap = np.arange(-20, 550)
y_nB_extrap = expo(x_extrap, *params_nB)  # Without Bolt.
y_B_extrap = expo(x_extrap, *params_all)  # With Bolt.

# Create a plot of the world record times and the extrapolated curves.
fig, ax = plt.subplots()
ax.plot(x_all, y_all, '.', label='data', c='k')
ax.plot(x_extrap, y_nB_extrap, '-', label='fitted without Bolt')
ax.plot(x_extrap, y_B_extrap, '--', c='red', label='fitted with Bolt')
ax.set(title="Men's 100 m World Record Extrapolated",
       xlabel='Years Since First Record (1912)',
       ylabel='Time (s)',
       yticks=np.arange(9.0, 11.0, 0.2))
ax.grid(True)
ax.legend(framealpha=1)

# Add a dotted horizontal line for each of Bolt's world record times.
bolt_times = {2009: 9.58, 2008: 9.69}
for year, time in bolt_times.items():
    ax.axhline(time, ls=':', linewidth=1.3, color='red')
    ax.text(0, time + 0.01, f"Bolt {year}", color='red',
            horizontalalignment='left', size=9)

# Define function and inverse function to permit a secondary x-axis for year:
axis_transform = lambda x_extrap: x_extrap + 1912
axis_inverse = lambda x_extrap: x_extrap - 1912
ax2 = ax.secondary_xaxis('top', functions=(axis_transform, axis_inverse))

print(f"\nMinimum predicted time without Bolt data = {min(y_nB_extrap):.2f} sec.")
print(f"Minimum predicted time with Bolt data =    {min(y_B_extrap):.2f} sec.\n")

Minimum predicted time without Bolt data = 9.57 sec.
Minimum predicted time with Bolt data =    9.19 sec.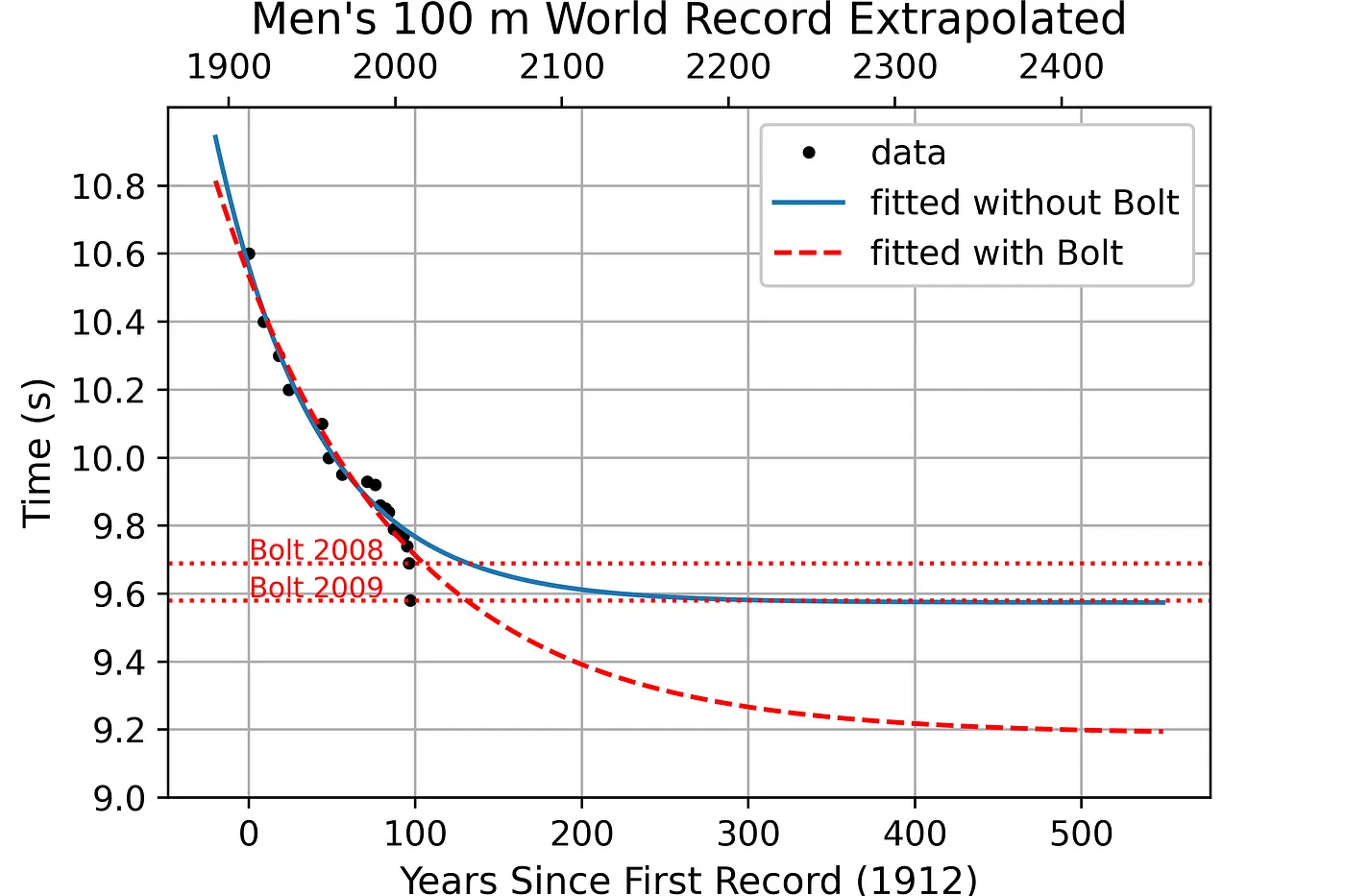

Две кривые, экстраполированные в будущее (изображение источника)

Технически обе кривые учитывают текущий рекорд Болта в 9,58 секунды. Если мы предположим, что красная кривая, включающая данные Болта, дает верный прогноз, то достижение Болта опередило график на десятилетия.

Красная кривая предсказывает, что максимальный человеческий предел в беге на 100 м составляет 9,19 секунды и будет достигнут примерно через 400 лет. Хотя 9,19 секунды, безусловно, являются быстрыми, они не расходятся с другими опубликованными прогнозами, такими как 9,27, 9,26 и 9,09 секунды [9][10][11].

И хотя 400 лет — это большой срок, некоторые исследователи полагают, что текущий рекорд Болта продержится еще 230 лет [2]! В любом случае, наши значения 9,57 и 9,19 секунды правдоподобны и имеют хорошие шансы попасть в скобки окончательного значения. Разве математика (и Python) не прекрасны?

Вывод

Многие природные явления, такие как радиоактивный распад, трещины в горных породах и рост населения, можно смоделировать математически с помощью таких инструментов, как экспоненциальные уравнения, степенные законы и логистические функции. Помимо сопоставления существующих данных, эти модели также могут прогнозировать будущее поведение. В этом проекте Quick Success Data Science мы использовали экспоненциальное уравнение, чтобы предсказать максимальное время бега на 100 м среди мужчин.

Подгонка кривых к данным требует манипулирования несколькими параметрами. Цель состоит в том, чтобы свести к минимуму ошибки между фактическими точками данных и прогнозируемыми точками данных. Библиотека Python SciPy включает функции, которые автоматизируют этот процесс и делают подбор кривых доступным для всех.

* * *

[1] Нормальное распределение

[2] Северо-Западный университет, Инженерная школа Маккормика: сколько времени потребуется, чтобы побить рекорд Усэйна Болта в беге на 100 метров? Профессор Луис Амарал подсчитывает шансы (2016 г.).

[3] Литтл, Браун и компания, Формула: универсальные законы успеха Альберта-Ласло Барабаши (2018).

[4] Экспоненциальное затухание. (2023, 11 марта). В Википедии.

[5] SciPy: https://scipy.org/ (2023).

[6] Роберт Вуд, «Мировые рекорды на 100 м». Веб-сайт Topend Sports, 2008 г., https://www.topendsports.com/sport/athletics/record-100m.htm, по состоянию на 1 мая 2023 г.

[7] Усэйн Болт. (2023, 15 апреля). В Википедии.

[8] Wired: Болт невероятно быстр, но далеко не человеческий предел Алексис Мадригал (2008).

[9] Мир бегуна: максимальное время на 100 метров: 9,27 секунды? Эмби Берфут (2014).

[10] Idea & Issac: Femto Essays: World Records for Men’s 100 m Defy Simple Curve Fitting Тацуо Табата (2008).

[11] Idea & Issac: Femto Essays: Мировой рекорд Болта снова меняет эмпирическое предсказание, Тацуо Табата (2009).