Merge Sort в Python 

Merge Sort - один из самых известных алгоритмов сортировки. Если вы изучаете информатику, Merge Sort вместе с Quick Sort, вероятно, является первым эффективным алгоритмом сортировки общего назначения, о котором вы слышали. Это также классический пример алгоритма «разделяй и властвуй».

Сортировка слиянием

Способ сортировки слиянием работает так:

Исходный массив делится на две примерно равные части. Если массив имеет нечетное количество элементов, одна из этих «половин» на один элемент больше, чем другая.

Подмассивы делятся снова и снова на две половины, пока вы не получите массивы, которые имеют только один элемент.

Затем вы объединяете пары одноэлементных массивов в двухэлементные массивы, сохраняя их в процессе. Затем эти отсортированные пары объединяются в четырехэлементные массивы и так далее до тех пор, пока не будет получен исходный отсортированный массив.

Вот визуализация сортировки слиянием:

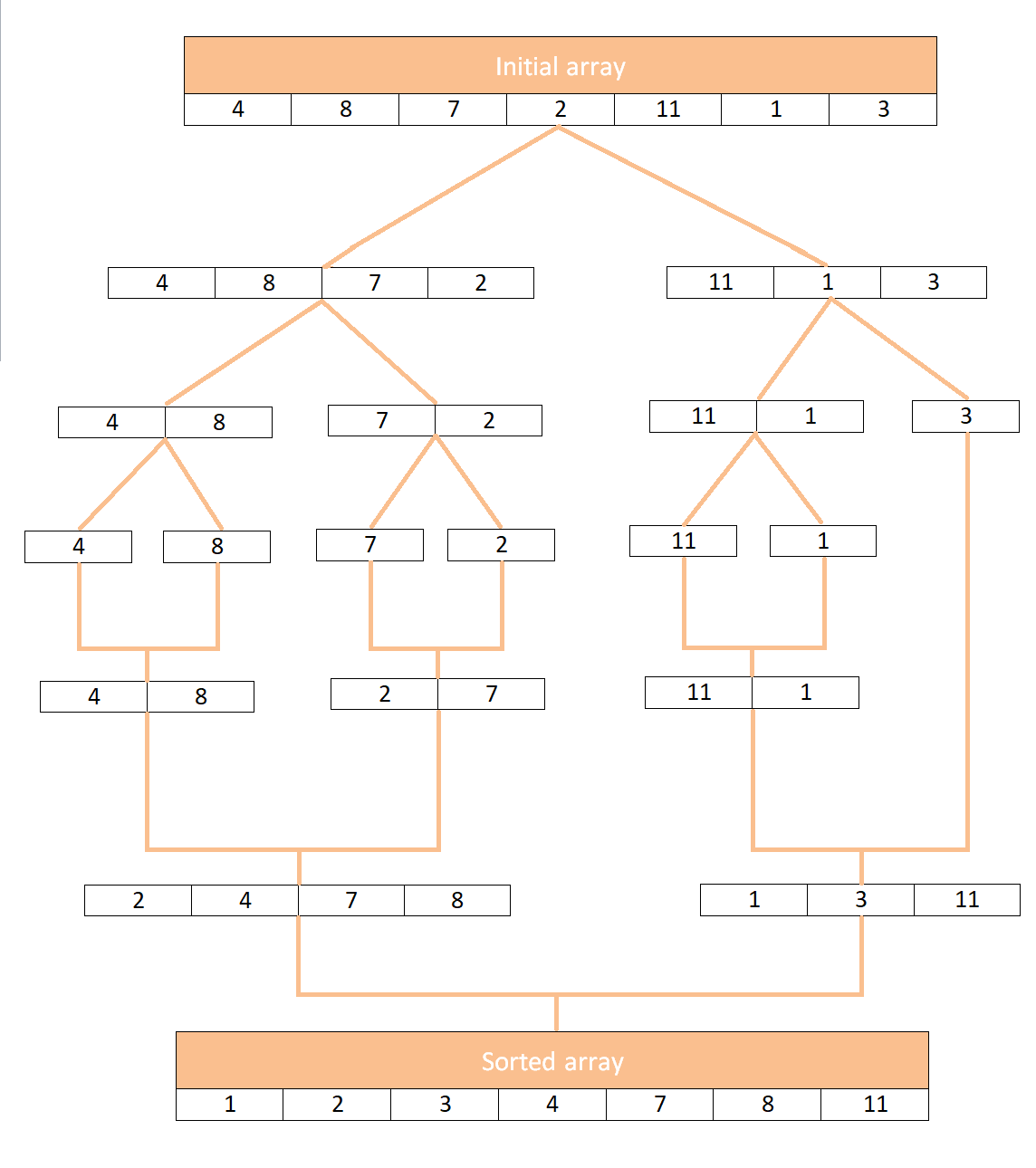
Как вы можете видеть, тот факт, что массив не может быть разделен на равные половины, не является проблемой, 3 просто «ждет», пока не начнется сортировка.

Существует два основных способа реализации алгоритма сортировки слиянием, один из которых - использование подхода сверху вниз, как в приведенном выше примере, и именно так чаще всего вводится сортировка слиянием.

Другой подход, то есть восходящий , работает в обратном направлении, без рекурсии (работает итеративно) - если наш массив имеет N элементов, мы делим его на N подмассивов одного элемента и сортируем пары смежных одноэлементных массивов, затем сортируем соседние пары двухэлементных массивов и т.д.

Примечание: снизу вверх подход обеспечивает интересную оптимизацию, которую мы будем обсуждать позже. Мы будем реализовывать нисходящий подход, так как это более простые и интуитивно понятные пары с тем фактом, что между ними нет реальной разницы во временной сложности без особых оптимизаций.

Основная часть обоих этих подходов заключается в том, как мы объединяем два меньших массива в один. Это сделано довольно интуитивно, скажем, мы рассмотрим последний шаг в нашем предыдущем примере. У нас есть массивы:

1. A: 2 4 7 8
2. Б: 1 3 11
3. отсортировано: None

Первое, что мы сделаем, это посмотрим на первый элемент обоих массивов. Мы находим тот, который меньше, в нашем случае это 1 , так что это первый элемент нашего отсортированного массива, и мы продвигаемся вперед в массиве B :

1. A: 2 4 7 8
2. Б: 1 3 11
3. отсортировано: 1

Затем мы смотрим на следующую пару элементов 2 и 3 ; 2 меньше , поэтому мы помещаем его в наш отсортированный массив и двигаться вперед в массиве A . Конечно, мы не двигаемся вперед в массиве B и держим указатель на 3 для будущих сравнений:

1. A: 2 4 7 8
2. Б: 1 3 11
3. отсортировано: 1 2

Используя ту же логику, мы перемещаемся по остальным и получаем массив {1, 2, 3, 4, 7, 8, 11}.

Возможны два особых случая:

1. Оба подмассива имеют одинаковый элемент. Мы можем двигаться вперед в любом из них и добавить элемент в отсортированный массив. Мы можем технически продвинуться вперед в обоих массивах и добавить оба элемента в отсортированный массив, но это потребует особого поведения, когда мы встретим одинаковые элементы в обоих массивах.
2. Мы "исчерпали" элементы в одном подмассиве. Например, у нас есть массив с {1, 2, 3} и массив с {9, 10, 11}. Очевидно, что мы пройдемся по всем элементам первого массива, не продвигаясь вперед ни разу во втором. Всякий раз, когда у нас заканчиваются элементы в подмассиве, мы просто добавляем элементы второго за другим.

Имейте в виду, что мы можем сортировать по своему усмотрению - этот пример сортирует целые числа в порядке возрастания, но мы можем так же легко сортировать в порядке убывания или сортировать пользовательские объекты.

Реализация

Мы будем реализовывать сортировку слиянием для двух типов коллекций - для массивов целых чисел (обычно используемых для представления сортировки) и для пользовательских объектов (более практичный и реалистичный сценарий).

Мы реализуем алгоритм сортировки слиянием, используя подход сверху вниз. Алгоритм не выглядит очень «симпатичным» и может сбить с толку, поэтому мы подробно рассмотрим каждый шаг.

Сортировка массивов

Начнем с простой части. Основная идея алгоритма состоит в том, чтобы разделить подмассивы пополам и отсортировать их рекурсивно. Мы хотим продолжать делать это как можно больше, то есть до тех пор, пока не получим подмассивы, которые имеют только один элемент:

def merge_sort(array, left_index, right_index):
    if left_index > right_index:
        return

    middle = (left_index + right_index) // 2
    merge_sort(array, left_index, middle)
    merge_sort(array, middle + 1, right_index)
    merge(array, left_index, right_index, middle)

Вызывая метод merge последним, мы гарантируем, что все деления произойдут до того, как мы начнем сортировку. Мы используем оператор //, чтобы явно указать тот факт, что мы хотим целочисленные значения для наших индексов.

Следующим шагом является фактическая часть слияния через несколько шагов и сценариев:

1. Создайте копии наших массивов. Первый массив является подмассивом из, [left_index,..,middle] а второй из [middle+1,...,right_index]
2. Мы просматриваем обе копии (отслеживая указатели в обоих массивах), выбирая меньший из двух элементов, на которые мы сейчас обращаем внимание, и добавляем их в наш отсортированный массив. Мы перемещаемся вперед в любом массиве, из которого мы выбрали элемент, и вперед в отсортированном массиве.
3. Если у нас закончились элементы в одной из наших копий - просто добавьте оставшиеся элементы в другой копии в отсортированный массив.

С нашими изложенными требованиями, давайте продолжим и определим функцию merge():

def merge(array, left_index, right_index, middle):
    # Сделайте копии обоих массивов, которые мы пытаемся объединить

    # Увеличиваем второй параметр на 1
    left_copy = array[left_index:middle + 1]
    right_copy = array[middle+1:right_index+1]

    # Начальные значения для переменных, которые мы используем для хранения
    # Курсор того, где мы находимся в каждом массиве
    left_copy_index = 0
    right_copy_index = 0
    sorted_index = left_index

    # Пройдите обе копии, пока у нас не закончатся элементы
    while left_copy_index < len(left_copy) and right_copy_index < len(right_copy):

        if left_copy[left_copy_index] <= right_copy[right_copy_index]:
            array[sorted_index] = left_copy[left_copy_index]
            left_copy_index = left_copy_index + 1
        else:
            array[sorted_index] = right_copy[right_copy_index]
            right_copy_index = right_copy_index + 1

        sorted_index = sorted_index + 1

    # У нас закончились элементы в left_copy или right_copy
    # так что мы пройдемся по оставшимся элементам и добавим их
    while left_copy_index < len(left_copy):
        array[sorted_index] = left_copy[left_copy_index]
        left_copy_index = left_copy_index + 1
        sorted_index = sorted_index + 1

    while right_copy_index < len(right_copy):
        array[sorted_index] = right_copy[right_copy_index]
        right_copy_index = right_copy_index + 1
        sorted_index = sorted_index + 1

Теперь давайте проверим нашу программу:

array = [33, 42, 9, 37, 8, 47, 5, 29, 49, 31, 4, 48, 16, 22, 26]
merge_sort(array, 0, len(array) -1)
print(array)

И вывод:

[4, 5, 8, 9, 16, 22, 26, 29, 31, 33, 37, 42, 47, 48, 49]

Сортировка пользовательских объектов

Теперь, когда у нас есть основной алгоритм, мы можем посмотреть, как сортировать пользовательские классы. Мы можем переопределить __eq__, __le__, __ge__ и другие операторы, как необходимые для этого.

Это позволяет нам использовать тот же алгоритм, что и выше, но ограничивает нас только одним способом сортировки наших пользовательских объектов, что в большинстве случаев не то, что мы хотим. Лучшая идея - сделать сам алгоритм более универсальным и вместо него передать ему функцию сравнения.

Сначала мы реализуем пользовательский класс Car и добавим в него несколько полей:

class Car:
    def __init__(self, make, model, year):
        self.make = make
        self.model = model
        self.year = year

    def __str__(self):
        return str.format("Make: {}, Model: {}, Year: {}", self.make, self.model, self.year)

Затем мы внесем несколько изменений в наши методы сортировки слиянием. Самый простой способ достичь того, чего мы хотим, это использовать лямбда-функции. Вы можете видеть, что мы только добавили дополнительный параметр и соответственно изменили вызовы метода, и только еще одну строку кода, чтобы сделать этот алгоритм намного более универсальным:

def merge(array, left_index, right_index, middle, comparison_function):
    left_copy = array[left_index:middle + 1]
    right_copy = array[middle+1:right_index+1]

    left_copy_index = 0
    right_copy_index = 0
    sorted_index = left_index

    while left_copy_index < len(left_copy) and right_copy_index < len(right_copy):

        # Мы используем comparison_function вместо простого оператора сравнения
        if comparison_function(left_copy[left_copy_index], right_copy[right_copy_index]):
            array[sorted_index] = left_copy[left_copy_index]
            left_copy_index = left_copy_index + 1
        else:
            array[sorted_index] = right_copy[right_copy_index]
            right_copy_index = right_copy_index + 1

        sorted_index = sorted_index + 1

    while left_copy_index < len(left_copy):
        array[sorted_index] = left_copy[left_copy_index]
        left_copy_index = left_copy_index + 1
        sorted_index = sorted_index + 1

    while right_copy_index < len(right_copy):
        array[sorted_index] = right_copy[right_copy_index]
        right_copy_index = right_copy_index + 1
        sorted_index = sorted_index + 1


def merge_sort(array, left_index, right_index, comparison_function):
    if left_index >= right_index:
        return

    middle = (left_index + right_index)//2
    merge_sort(array, left_index, middle, comparison_function)
    merge_sort(array, middle + 1, right_index, comparison_function)
    merge(array, left_index, right_index, middle, comparison_function)

Давайте протестируем или модифицируем алгоритм в нескольких случаях Car:

car1 = Car("Alfa Romeo", "33 SportWagon", 1988)
car2 = Car("Chevrolet", "Cruze Hatchback", 2011)
car3 = Car("Corvette", "C6 Couple", 2004)
car4 = Car("Cadillac", "Seville Sedan", 1995)

array = [car1, car2, car3, car4]

merge_sort(array, 0, len(array) -1, lambda carA, carB: carA.year < carB.year)

print("Cars sorted by year:")
for car in array:
    print(car)

print()
merge_sort(array, 0, len(array) -1, lambda carA, carB: carA.make < carB.make)
print("Cars sorted by make:")
for car in array:
    print(car)

Мы получаем вывод:

Cars sorted by year:
Make: Alfa Romeo, Model: 33 SportWagon, Year: 1988
Make: Cadillac, Model: Seville Sedan, Year: 1995
Make: Corvette, Model: C6 Couple, Year: 2004
Make: Chevrolet, Model: Cruze Hatchback, Year: 2011

Cars sorted by make:
Make: Alfa Romeo, Model: 33 SportWagon, Year: 1988
Make: Cadillac, Model: Seville Sedan, Year: 1995
Make: Chevrolet, Model: Cruze Hatchback, Year: 2011
Make: Corvette, Model: C6 Couple, Year: 2004

Оптимизация

Давайте уточним разницу между сортировкой слиянием сверху вниз и снизу вверх. Восходящий принцип работает подобно второй половине нисходящего подхода, в котором вместо рекурсивного вызова сортировки по подмассивам мы итеративно сортируем соседние подмассивы.

Одна вещь, которую мы можем сделать, чтобы улучшить этот алгоритм, это рассмотреть отсортированные куски вместо отдельных элементов, прежде чем разбивать массив.

Это означает, что для данного массива, такого как {4, 8, 7, 2, 11, 1, 3}, вместо разбиения его на {4}, {8}, {7}, {2}, {11}, {1}, {3} - он разделен на подмассивы, которые уже могут быть отсортированы: {4,8}, {7}, {2,11}, {1,3}, а затем отсортированы.

С реальными данными у нас часто есть много этих уже отсортированных подмассивов, которые могут заметно сократить время выполнения сортировки слиянием.

С сортировкой слиянием следует учитывать еще одну вещь, особенно нисходящую версию - многопоточность. Сортировка слиянием удобна для этого, поскольку каждая половина может быть отсортирована независимо от ее пары. Единственное, в чем мы должны убедиться, это то, что мы закончили сортировку каждой половины, прежде чем объединить их.

Сортировка слиянием, однако, относительно неэффективна (как во времени, так и в пространстве), когда дело доходит до меньших массивов, и часто оптимизируется путем остановки, когда мы достигаем массива ~ 7 элементов, вместо того, чтобы переходить к массивам с одним элементом, и вызывать сортировку вставкой вместо этого рассортируйте их, прежде чем объединить в больший массив.

Это связано с тем, что сортировка вставками действительно хорошо работает с небольшими и / или почти отсортированными массивами.

Вывод

Merge Sort - эффективный алгоритм сортировки общего назначения. Его основным преимуществом является надежное время выполнения алгоритма и его эффективность при сортировке больших массивов. В отличие от Quick Sort, это не зависит от каких-либо неудачных решений, которые приводят к плохому времени выполнения.

Одним из основных недостатков является дополнительная память, которую сортировка слиянием использует для хранения временных копий массивов перед их объединением. Тем не менее, Merge Sort является отличным, интуитивно понятным примером для ознакомления будущих инженеров-программистов с подходом «разделяй и властвуй» к созданию алгоритмов.