Сортировка слиянием в JavaScript

Сортировка относится к расположению элементов списка в определенном порядке (числовом или буквенном). Сортировка обычно используется вместе с поиском.
Как правило, легче искать элемент (называемый ключом) в данном списке, если список отсортирован как визуально, так и алгоритмически.
Существует много способов (алгоритмов) сортировки заданного списка элементов. Сортировка слиянием - один из наиболее популярных и эффективных способов сделать это.
В этой статье мы увидим логику сортировки слиянием, реализуем ее на JavaScript и визуализируем в действии. Наконец, мы сравним сортировку слиянием с другими алгоритмами с точки зрения пространственной и временной сложности.
Понимание логики сортировки слиянием
Сортировка слиянием использует концепцию «разделяй и властвуй» для сортировки заданного списка элементов. Он разбивает проблему на более мелкие подзадачи, пока они не станут достаточно простыми для непосредственного решения.
Вот шаги, которые выполняет сортировка слиянием:
- Разделите данный список на две половины (примерно равные половины в случае списка с нечетным числом элементов).
- Продолжайте разделять подмассивы таким же образом, пока у вас не останутся только одноэлементные массивы.
- Начиная с массивов с одним элементом, объедините подмассивы, чтобы отсортировать каждый объединенный подмассив.
- Повторите шаг 3 с одним отсортированным массивом.
Давайте посмотрим, как сортировка слиянием работает с такими массивами, как [4, 8, 7, 2, 11, 1, 3]:
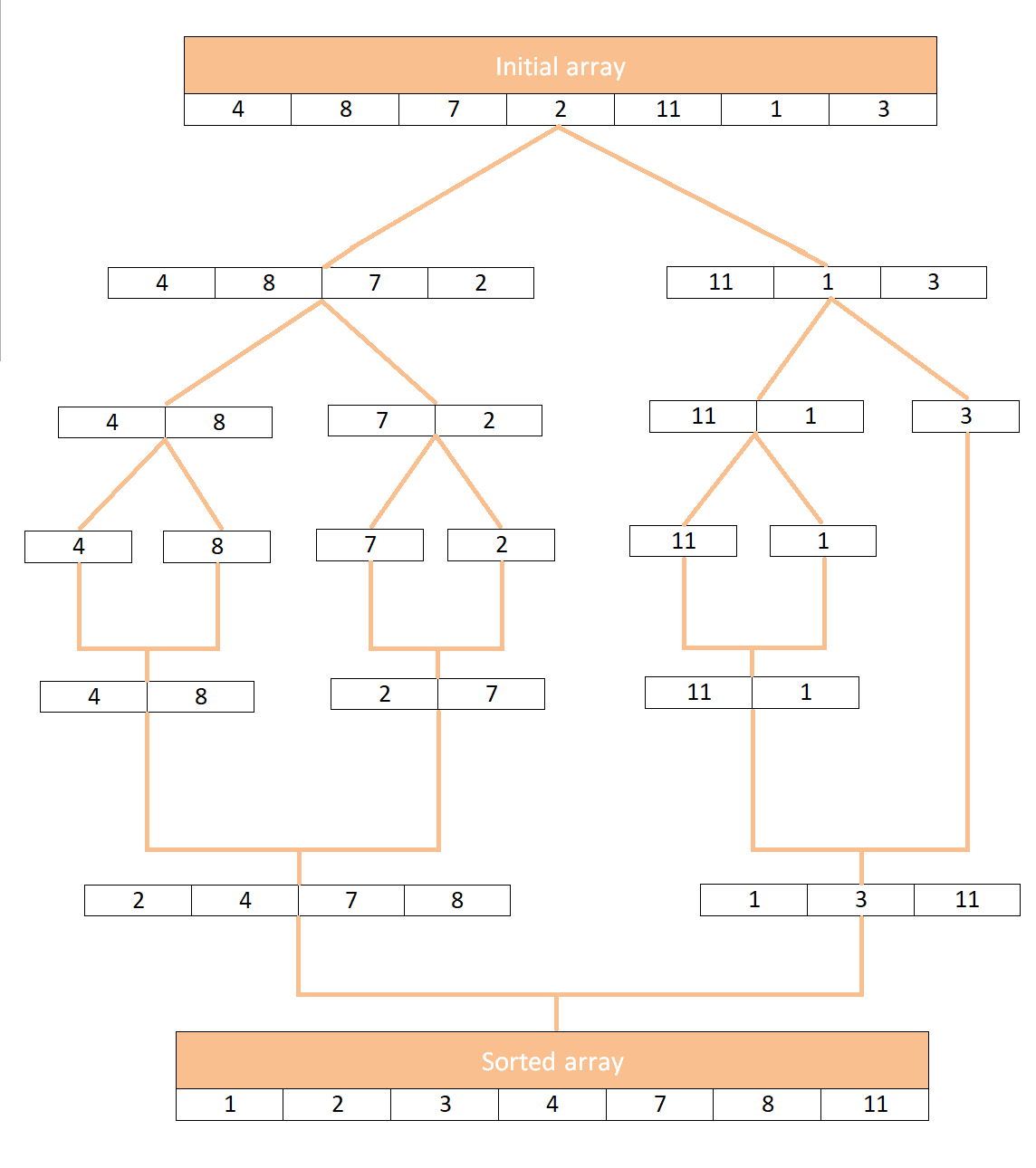
Реализация сортировки слиянием в JavaScript
Давайте сначала напишем код для двух отсортированных подмассивов в отсортированный массив. Очень важно иметь в виду, что оба подмассива уже отсортированы, и мы просто прочесываем их с помощью функции merge().
Мы можем сделать это, пройдя по обоим этим подмассивам и добавив один за другим элементы, чтобы полученный массив также был отсортирован:
function merge(left, right) {
let arr = []
// Break out of loop if any one of the array gets empty
while (left.length && right.length) {
// Pick the smaller among the smallest element of left and right sub arrays
if (left[0] < right[0]) {
arr.push(left.shift())
} else {
arr.push(right.shift())
}
}
// Concatenating the leftover elements
// (in case we didn't go through the entire left or right array)
return [ ...arr, ...left, ...right ]
}
В этой функции мы берем два отсортированных подмассива (left, right) и объединяем их, чтобы получить один отсортированный массив. Сначала мы создаем пустой массив. Позже мы выбираем меньший из самых маленьких невыделенных элементов в подмассивах и left и right помещаем их в пустой массив. Нам нужно только проверить первые элементы в left и right, так как они оба отсортированы.
При этом мы удаляем выбранный элемент из подмассива (это достигается с помощью функции shift()). Продолжаем этот процесс до тех пор, пока один из подмассивов не станет пустым. После этого мы помещаем оставшиеся элементы непустого подмассива (потому что они уже отсортированы) в основной массив.
Так мы теперь имеем код для слияния двух отсортированных массивов (властвуй из "разделяй и властвуй"), выпишем окончательный код для алгоритма сортировки слиянием. Это означает, что нам нужно продолжать разбивать массивы, пока мы не получим массивы, содержащие только один элемент:
function mergeSort(array) {
const half = array.length / 2
// Base case or terminating case
if(array.length < 2){
return array
}
const left = array.splice(0, half)
return merge(mergeSort(left),mergeSort(array))
}
Здесь мы определяем среднюю точку и разделяем массив на два подмассива с помощью функции splice(). Если есть нечетное количество элементов, левый получает меньшее количество элементов. Мы разделяем, пока не останемся с одноэлементными массивами (array.length < 2). После этого начинаем объединять подмассивы с помощью написанной ранее функции merge().
Теперь, когда у нас есть код, давайте посмотрим на результат выполнения функции из нашего предыдущего примера:
array = [4, 8, 7, 2, 11, 1, 3];
console.log(mergeSort(array));
Это дает нам ожидаемый результат:
1,2,3,4,7,8,11
Эффективность сортировки слиянием
Наихудшая временная сложность сортировки слиянием равна O(nlogn), такая же, как и для лучшей временной сложности для быстрой сортировки. Когда дело доходит до скорости, сортировка слиянием - один из самых быстрых алгоритмов сортировки.
В отличие от быстрой сортировки, сортировка слиянием не является алгоритмом сортировки на месте, что означает, что для нее требуется дополнительное пространство, кроме входного массива. Это потому, что мы используем вспомогательные массивы для хранения подмассивов. Пространственная сложность сортировки слиянием - O(n).
Еще одним преимуществом сортировки слиянием является то, что она очень хорошо подходит для многопоточности, поскольку каждая соответствующая половина сортируется отдельно.
Вывод
В этой статье мы увидели логику алгоритма сортировки слиянием, как реализовать его в JavaScript, и узнали о его производительности. Это один из основных алгоритмов сортировки, который действительно полезен для наглядного примера стратегии « разделяй и властвуй» .