Совершенная, бесконечная точность, игровая физика в Python (серия 1)

Это крошечный шаг в грандиозном стремлении превратить всю физику, математику и даже философию в программирование. Благодаря этому проекту мы откроем для себя сюрпризы, углубим наше понимание и повеселимся. Весь код доступен на GitHub.
Мы будем ограничивать движок многими способами — например, ньютоновскими столкновениями между окружностями и линиями. Однако мы не будем ограничивать точность двигателя. Он будет представлять все времена, положения и скорости с точными выражениями, такими как 8*sqrt(3)/3. Другими словами, это позволяет избежать всех численных приближений.
В результате получится идеальная имитация, например, игрушки-колыбели Ньютона.
Чем хорош физический движок с абсолютной точностью? Помимо прочего, это может улучшить наше понимание физического мира. Мы увидим эти новые открытия:
- Ограничение скорости теннисного мяча — В популярной демонстрации физики вы бросаете теннисный мяч баскетбольным мячом. Теннисный мячик подпрыгивает вверх гораздо быстрее, чем падает. Насколько быстрее? Мы увидим, что скорость «вверх» никогда не превышает скорость «вниз» более чем в три раза. Это справедливо, даже если мы сделаем баскетбольный мяч бесконечно массивным.
- Хорошие вибрации — Представьте движущийся теннисный мяч, зажатый между баскетбольным мячом и стеной. За короткое время между двумя кадрами видео теннисный мяч может подпрыгнуть 80 раз. Движок, использующий приближения, может пропустить некоторые из этих отскоков. Наш двигатель учитывает каждого из них.
Также, в следующей статье (серия 2):
- Бильярдный брейк — даже с бесконечной точностью бильярдный брейк практически невозможно обратить вспять. Мы увидим, что даже когда мы уберем «эффект бабочки» и квантовую неопределенность, мир по-прежнему остается случайным и недетерминированным.
Недостатком нашего идеального физического движка является скорость. Для большинства симуляций, по мере продвижения вперед во времени, выражения для времени, положения и скорости становятся более сложными. В бильярдном мире, который вы можете увидеть в серии 2, это ограничивает нашу симуляцию до 20 или около того «событий». (Мы определим «события» позже.) Можем ли мы увеличить скорость? Только немного.
Создание двигателя
Предположим, у нас уже есть функции Python для:
- Учитывая любые два (возможно, движущихся) объекта в мире, верните точный промежуток времени, пока они не соприкоснутся. Ответ может быть «никогда».
- Как именно столкновение изменит их скорость и направление при любых двух сталкивающихся объектах?
Мы увидим, как создавать такие функции в серии 3. А пока подумайте, как превратить эти функции в совершенный физический движок.
Давайте проработаем подход, рассмотрев три физических мира, начиная с Колыбели Ньютона.
Колыбель Ньютона
Общая идея нашего движка состоит в том, чтобы определить точное время до следующего столкновения в мире. Перенеситесь точно в это время. Отрегулируйте скорости сталкивающихся объектов. Повторяйте.
Для Колыбели Ньютона мы сначала установили круги и стены.
from perfect_physics import World, Circle, Wall
circle_list = [Circle(x=1, y=0, r=1, vx=1, vy=0, m=1)]
for i in range(1, 6):
circle_list.append(Circle(x=i * 2 + 4, y=0, r=1, vx=0, vy=0, m=1))
wall_list = [Wall(x0=0, y0=0, x1=0, y1=1), Wall(x0=20, y0=0, x1=20, y1=1)]
world = World(circle_list, wall_list, xlim=(-1, 21), ylim=(-2, 2))
world.show()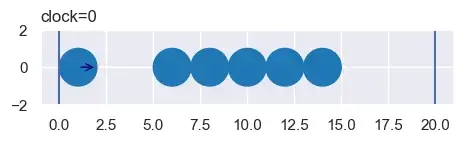
Далее:
- Между каждой парой объектов найдите точный промежуток времени, в течение которого они сталкиваются (если есть). Игнорируйте другие пары и столкновения. — В этом случае первый (движущийся) круг столкнется со вторым кругом в промежутке времени 3. Игнорируя это столкновение, он также столкнется с третьим кругом в промежутке времени 5 и т. д. Он столкнется с дальней стеной в момент времени размах 18.
- Найдите промежуток времени первого столкновения (столкновений) и переведите мировые часы ровно на это значение. В этом случае 3.
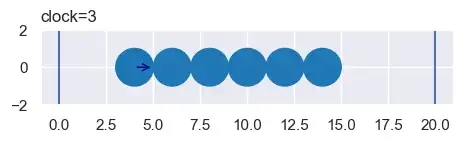
- Отрегулируйте скорости всех объектов, участвующих в этих столкновениях. Как и ожидалось в случае с Колыбелью Ньютона, первый круг становится неподвижным, а второй круг начинает двигаться.
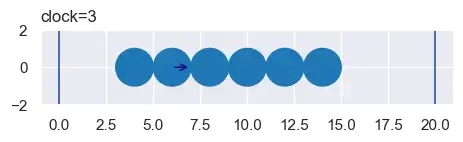
- Повторяйте столько, сколько хотите. В этом примере второй и третий мячи столкнутся во временном интервале 0. В этом видео показано действие, событие за событием. («Событие» — это либо перемещение времени вперед к столкновению, либо корректировка скорости в зависимости от столкновения)
Чтобы превратить эти события в обычное видео, нам нужно генерировать кадры с регулярными интервалами, например, каждые 1/24 секунды. Первый кадр покажет мир на часах 0. Поиграв с альтернативами, мы решили, что нам нужно 10 видеосекунд на единицу времени моделирования. Таким образом, второй кадр будет для часов 10/24 (он же 5/12). Мы знаем, что столкновения не будет до 3 часов, поэтому мы можем просто перемещать круг без учета столкновений. Его положение будет точным.
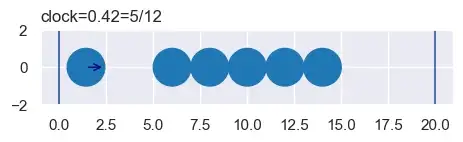
В общем, для каждого кадра мы:
- Найдите значение часов моделирования для этого кадра.
- Найдите событие столкновения, которое предшествует этому значению часов.
- Начиная с мира при предыдущем столкновении, переместите круги на значение часов кадра. (По замыслу, круги ни с чем не столкнутся во время этого перемещения.)
Все позиции и время указаны точно. Видео в начале статьи показывает результат.
Круг и треугольник
Я утверждаю, что время и позиции указаны точно, но верите ли вы мне? Вот некоторые доказательства с помощью круга, вписанного в треугольник. Во-первых, вот видео, показывающее только события. Вы можете видеть, что часы установлены в такие выражения, как 8*sqrt(3)/3.
А вот и обычное видео для круга в треугольнике:
В этом случае симуляция укладывается в шаблон. Без бесконечной точности шаблон можно было бы упустить.
Падение теннисного мяча и баскетбольного мяча
Давайте посмотрим еще на один физический мир, чтобы увидеть еще одно преимущество бесконечной точности. Этот мир включает в себя теннисный мяч и баскетбольный мяч, движущиеся к стене со скоростью 1. Масса баскетбольного мяча в 1000 раз больше массы теннисного мяча. (В наших мирах нет гравитации.)
from perfect_physics import World, Circle, Wall
big_radius = 10
world_width = 40
folder = root / f"part1/two_size{big_radius}"
big = Circle(x=world_width // 2, y=0, r=big_radius, vx=1, vy=0, m=big_radius**3)
little = Circle(x=big.x - big_radius - 1, y=0, r=1, vx=1, vy=0, m=1)
circle_list = [big, little]
wall_list = [Wall(x0=0, y0=0, x1=0, y1=1), Wall(x0=world_width, y0=0, x1=world_width, y1=1)]
world = World(circle_list, wall_list, xlim=(-1, world_width + 1), ylim=(-big_radius - 1, big_radius + 1))
world.run_in_place(2, show=True)
print([circle.vx for circle in world.circle_list])Ровно в 10-й момент мячи отскакивают от правой стены. Скорость теннисного мяча увеличивается с 1 до 2999/1001, а баскетбольного немного замедляется до 997/1001.
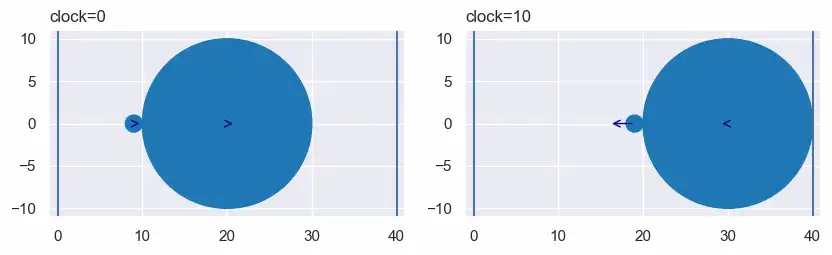
Как и ожидалось (если вы уже пробовали это в физическом мире), теннисный мяч ускоряется. Однако это удивило меня тем, что я ехал всего в три раза быстрее.
Давайте на мгновение забежим вперед и воспользуемся инструментами, которые мы разработаем в серии 3. Этот код на Python показывает влияние на теннисные мячи баскетбольного мяча с бесконечной массой. Теннисный мяч входит со скоростью 1 и выходит со скоростью ровно 3.
from sympy import limit, simplify, oo
from perfect_physics import load
cc_velocity_solution = load("data/cc_velocity_solution.sympy")
a_vx, a_vy, b_vx, b_vy = cc_velocity_solution.subs([("a_x", 10), ("a_y", 0), ("a_r", 10), ("a_vx", -1), ("a_vy", 0),
("b_x", -1), ("b_y", 0), ("b_r", 1), ("b_vx", 1), ("b_vy", 0), ("b_m", 1)])
print(simplify(b_vx))
limit(b_vx, "a_m", oo)
# prints (1 - 3*a_m)/(a_m + 1)
# returns -3Если, вы ожидали, что теннисный мяч разогнется до бесконечности, то, вы узнали кое-что о физике реального мира из этого физического движка.
Двигатель удивляет нас еще больше, когда мы дали ему поработать дольше. Посмотрите, что происходит во время видео 20 секунд (время моделирования 200):
Баскетбольный мяч раздавливает теннисный мяч. Это приводит к тому, что теннисный мяч отскакивает назад и вперед более 80 раз за один видеокадр. Теннисный мяч достигает скорости, превышающей 31. На звуковой дорожке видео вибрация теннисного мяча создает звуковой сигнал частотой более 2000 Гц (ударов в секунду).
Если бы вместо точного расчета мы просто делали выборку один раз за кадр, мы бы пропустили (или просчитались) это быстрое действие.
Подводим итоги
У нас есть идеальный физический движок. Мы превратили немного физики в программирование.
Мы предположили, что начали с двух функций Python, которые сообщают нам — для любой пары объектов — две вещи: 1) Время до их следующего столкновения (если таковое имеется) и 2) Влияние этого столкновения на их скорости. Мы увидели, как превратить эти две функции в совершенный физический движок, многократно перемещаясь вперед во времени до следующего столкновения и регулируя скорости всех объектов, участвующих в столкновении.
Мы создавали видео, просматривая столкновение, предшествовавшее видеокадру, а затем перемещая время вперед (не беспокоясь о столкновениях) до этого кадра.
Колыбель Ньютона, первый мир, вела себя так, как и ожидалось. Второй мир, круг, вписанный треугольником, используя такие выражения, как 8*sqrt(3)/3 для времени и т.д., нашли закономерность. Падение мячей теннисного и баскетбольного выявило неожиданное для нас ограничение скорости теннисного мяча. Кроме того, он производил отскоки быстрее, чем могли бы рассчитать менее совершенные методы.
Следующая статья, серия 2, имитирует бильярдный брейк с удивительными философскими результатами. Далее, в серии 3, мы увидим, как заставить компьютер создать эти две стартовые функции.