Совершенная, бесконечная точность, игровая физика в Python (серия 3)

Эта статья о том, как заставить компьютер выполнять математику за нас. Не только численные вычисления, но и алгебраические манипуляции и связанные с математическим анализом. Весь код доступен на GitHub.
Это полезно, потому что:
- Возможно, вы не помните всю математику, которую проходили в средней школе и колледже
- В школе наши учителя ставили нам только те задачи, которые мы могли решить. Сейчас же хотелось бы решать проблемы, которые не поддаются решению.
Вспомним, что в серии 1 и серии 2 этой серии мы разработали верхний уровень совершенного физического движка. Он использует такие выражения, как 175–9*sqrt(3)/2, для точного представления времени, положения и скорости, то есть без каких-либо приближений. Мы применили двигатель к Колыбе́ли Ньютона, к падению теннисного мяча и баскетбольного мяча, а также к бильярдному брейку. Моделирование привело к удивительным для нас открытиям в области физики и даже философии.
Здесь мы будем использовать компьютер для получения необходимых выражений из основных законов физики. Мы выполним эту работу в пять этапов:
- Смоделируем два движущихся круга. Используем SymPy, чтобы точно определить, когда два движущихся круга «просто коснутся». Узнаем, почему SymPy возвращает несколько ответов.
- Смоделируем круг и стену. Найдем, когда они просто коснутся. Добавим «секретное» шестое уравнение об углах (но не используйте углы).
- Смоделируем столкновения круг-круг с сохранением импульса и энергии. Добавим «секретное» четвертое уравнение об углах (но не используем углы).
- Предположим, что стены имеют бесконечную массу. Круг, отскакивающий от стены, нарушает закон сохранения импульса. Исправим это с помощью
limit. - Два объекта могут соприкасаться и в то же время удаляться друг от друга. Используем
limit, чтобы найти их. Удалим их из списка сталкивающихся объектов.
Начинаем с двух кругов.
Шаг 1: Смоделируем два движущихся круга. Используем SymPy, чтобы точно определить, когда два движущихся круга «просто коснутся». Узнаем, почему SymPy возвращает несколько ответов.
Мы собираемся смоделировать мир в виде кругов, движущихся по бесконечной двумерной плоскости. Круги движутся с постоянной скоростью, пока не столкнутся. Круги могут натыкаться друг на друга или на стены. Стены - это (бесконечно длинные) линии.
Первый вопрос, на который нам нужно ответить, - это когда (если вообще когда-либо) два движущихся круга просто начнут соприкасаться. Чтобы ответить на этот вопрос, мы разработаем набор уравнений. Затем мы попросим компьютер решить уравнения и дать нам ответ.
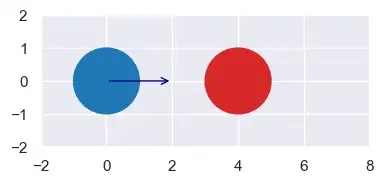
Чтобы сформулировать наше первое уравнение, подумайте о двух окружностях, a и b. У каждой есть положение (x, y), скорость (vx, vy) и радиус r. Можете ли вы предсказать будущее положение окружности (x’, y’) для любого времени t?
Наше первое уравнение гласит, что положение x окружности a в момент времени t равно ее текущему положению x плюс ее скорость vx, умноженная на время t. В математических обозначениях:
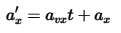
Уравнение 2 покажет нам положение окружности a по y в будущем. Уравнения 3 и 4 укажут нам положение b по x и y в будущем.
В качестве первого шага к превращению математики в программирование мы напишем эти четыре уравнения с помощью пакета SymPy на Python. SymPy - это система компьютерной алгебры, похожая на Mathematica и Maple. Однако, в отличие от этих систем, SymPy бесплатна и доступна внутри Python.
#1: Не путайте SymPy (пакет Python для символьной математики) с SimPy (пакет Python для моделирования).
#2: Системы компьютерной алгебры представляют выражения в виде вложенных компьютерных объектов. Это “символическое” представление упрощает некоторые задачи для компьютера — например, работу с дробями или получение производных от других выражений. Даже при символическом представлении некоторые задачи остаются трудными для компьютера — например, вычисление интегралов или решение систем нелинейных уравнений. Это связано с тем, что легко и трудно для людей. Мне нравится использовать системы компьютерной алгебры, потому что они лучше меня справляются с большинством задач, как легких, так и сложных.
Вот наши четыре уравнения в Python и SymPy:
from sympy import symbols, Eq
# define symbols
t = symbols("t")
a_x, a_y, a_vx, a_vy, a_r, aprime_x, aprime_y = symbols("a_x, a_y, a_vx, a_vy, a_r, a'_x, a'_y")
b_x, b_y, b_vx, b_vy, b_r, bprime_x, bprime_y = symbols("b_x, b_y, b_vx, b_vy, b_r, b'_x, b'_y")
# define equations
eq1 = Eq(aprime_x, a_x + a_vx * t)
eq2 = Eq(aprime_y, a_y + a_vy * t)
eq3 = Eq(bprime_x, b_x + b_vx * t)
eq4 = Eq(bprime_y, b_y + b_vy * t)pНам все еще нужно разработать понятие двух кругов, «просто соприкасающихся». Мы делаем это с помощью пятого уравнения. В нем говорится, что две окружности просто соприкасаются, когда расстояние между их центрами равно сумме радиусов. (Мы избегаем функции sqrt, возводя в квадрат обе стороны.) В математических обозначениях:
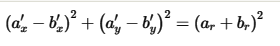
На Python и SymPy:
eq5 = Eq((aprime_x - bprime_x) ** 2 + (aprime_y - bprime_y) ** 2,
(a_r + b_r)**2)
Если мы дадим первым четырем уравнениям информацию о двух окружностях и времени, они сообщат нам положения окружностей в это время. Тогда уравнение пять может рассказать нам о двух кругах, которые в это время просто соприкасаются.
Другими словами, при заданном времени эти уравнения могут ответить на вопрос «Соприкасаются ли эти две окружности в момент t?» Но это не то, чего мы хотим. Мы хотим вывернуть это наизнанку и ответить на вопрос: «В какое время эти два круга просто соприкоснутся?»
Чтобы ответить на интересующий вопрос, математика говорит нам просто «решить» уравнения. К сожалению, «математика (которая решает уравнения, содержащие квадраты) сложна». К счастью, математика для SymPy несложна:
from sympy import nonlinsolve
from perfectphysics import savecc_all_solutions = nonlinsolve([eq1, eq2, eq3, eq4, eq5], t, aprime_x, aprime_y, bprime_x, bprime_y)
cc_time_solutions = [t for t, aprime_x, ap_y, bp_x, bp_y in cc_all_solutions]
save(cc_time_solutions, "cc_time_solutions.sympy")
cc_time_solutions[0]Примерно за 30 секунд просто находит два общих, символических решения. Вот лишь часть первого решения, cc_time_solutions[0] в математической нотации:

Нам это кажется сложным. Однако для компьютера это не сложно.
Почему существует два решения? Оценка их может помочь нам понять. Рассмотрим такую ситуацию: два круга радиусом 1 с синим шаром, движущимся со скоростью 2:
from perfect_physics import Circle, plot
a = Circle(x=0,y=0,r=1,vx=2,vy=0)
b = Circle(x=4,y=0,r=1,vx=0,vy=0)
plot([a, b], colors=["tab:blue","tab:red"], xlim=(-2,8), ylim=(-2,2), figsize=(4,2), font_scale=1)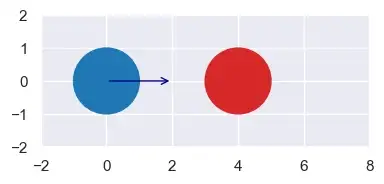
Мы используем метод SymPy .subs (замена), чтобы найти два момента, когда окружности a и b просто соприкоснутся. В это время мы также рисуем круги.
from perfect_physics import load
cc_time_solutions = load("cc_time_solutions.sympy")
times = [time_solution.subs([("a_x", a.x), ("a_y", a.y), ("a_r", a.r), ("a_vx", a.vx), ("a_vy", a.vy),
("b_x", b.x), ("b_y", b.y), ("b_r", b.r), ("b_vx", b.vx), ("b_vy", b.vy)])
for time_solution in cc_time_solutions]
print(times)
for time in times:
plot([a.tick_clone(time), b.tick_clone(time)], clock=time,
colors=["tab:blue","tab:red"], xlim=(-2,8), ylim=(-2,2), figsize=(4,2), font_scale=1)Python печатает [3, 1] и отображает:
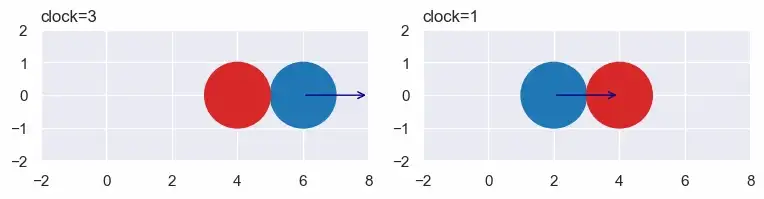
Другими словами, в момент 3 (игнорируя столкновения) синий круг будет просто касаться красного. Аналогично, в момент 1. Если нам нужно время до следующего столкновения, мы просто берем меньшее время, верно?
К сожалению, меньшее время тоже может оказаться неподходящим. Рассмотрим эту ситуацию, в которой круги удаляются друг от друга. Когда они просто соприкоснутся?
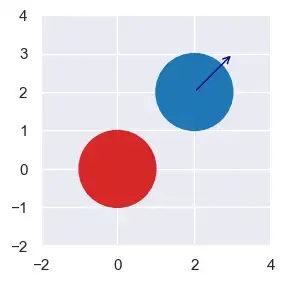
a = Circle(x=2,y=2,r=1,vx=1,vy=1)
b = Circle(x=0,y=0,r=1,vx=0,vy=0)
plot([a, b], colors=["tab:blue","tab:red"], xlim=(-2,4), ylim=(-2,4), figsize=(3,3), font_scale=1)
times = [time_solution.subs([("a_x", a.x), ("a_y", a.y), ("a_r", a.r), ("a_vx", a.vx), ("a_vy", a.vy),
("b_x", b.x), ("b_y", b.y), ("b_r", b.r), ("b_vx", b.vx), ("b_vy", b.vy)])
for time_solution in cc_time_solutions]
print(times)Python отвечает [-2 + sqrt(2), -2 — sqrt(2)]. (Обратите внимание, что он отвечает с бесконечной точностью, а не с чем-то приблизительным, таким как [-0.59, -3.41]). Эти времена отрицательные, что означает, что круги просто соприкоснутся в прошлом. Нас не волнуют прошлые столкновения, поэтому мы игнорируем негативные моменты.
Подводя итог: ответ даст нам два раза, и мы сохраняем наименьшее, неотрицательное время, верно? Неа. Мы также должны остерегаться еще двух осложнений. Во-первых, когда круги неподвижны или движутся вместе с одинаковой скоростью, время будет [nan, nan], то есть с плавающей запятой «не число».
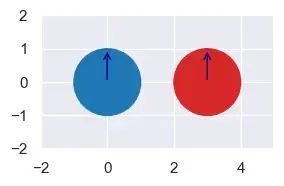
Во—вторых, когда круги движутся так, что их пути никогда не пересекаются, времена будут примерно такими [2 + sqrt(2)*I, 2 — sqrt(2)*I], содержащими мнимые числа.
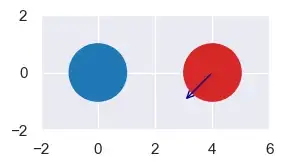
В конце концов, наша процедура заключается в том, чтобы просто получить два раза, а затем:
- отфильтруйте ответы, содержащие мнимые числа
- отфильтруйте ответы nan
- отфильтруйте отрицательные ответы
- сохраните наименьший оставшийся ответ (если таковой имеется)
Будет ли этот результат тем временем с бесконечной точностью следующего столкновения, которого мы желаем? Почти. Когда он говорит, что они просто соприкоснутся в нулевое время, круги могут удаляться друг от друга. Это ситуация, которая не считается столкновением.
Обратите внимание, что если мы можем обрабатывать два круга, мы можем обрабатывать любое количество кругов. Нам просто нужно посмотреть на все пары кругов и вернуть наименьшее время (если таковое имеется).
То, что мы сделали на этом этапе, очень круто. Нам просто нужно было составить пять простых уравнений о кругах, движущихся вперед во времени и проверяющих расстояние. Затем пакет Python SymPy выполнил за нас сложную математику. Он создал функцию, которая точно сообщает нам, когда (если вообще когда-либо) круги соприкоснутся.
На шаге 3 мы увидим, как прикосновение изменяет скорость каждого круга. Однако затем давайте поработаем с SymPy, чтобы определить, когда круг упрется в стену.
Шаг 2: Смоделируем круг и стену. Найдем, когда они просто коснутся. Добавим «секретное» шестое уравнение об углах (но не используйте углы).
Предположим, у нас есть круг a и стена w. Как и прежде, окружность имеет положение (x, y), скорость (vx, vy) и радиус r. Стена представляет собой (бесконечно длинную) линию. Мы задаем стену с любыми двумя различными точками вдоль нее, (x0, y0) и (x1, y1).
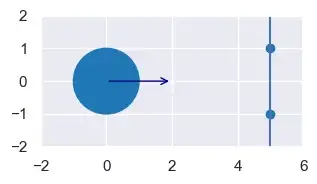
Чтобы определить, когда круг и стена просто соприкоснутся, мы снова моделируем положение круга (x’, y’) в момент времени t.
from sympy import symbols, Eq
t = symbols("t")
a_x, a_y, a_vx, a_vy, a_r, aprime_x, aprime_y = symbols("a_x, a_y, a_vx, a_vy, a_r, a'_x, a'_y")
eq1 = Eq(aprime_x, a_x + a_vx * t)
eq2 = Eq(aprime_y, a_y + a_vy * t)Далее мы моделируем место на стене, где круг и стена будут соприкасаться. Назовем эту точку (x2, y2). Это будет некоторая пропорция p между точками, определяющими стену (x0, y0) и (x1, y1). Например, если p равно 1/2, то (x2, y2) является средней точкой двух точек, определяющих стену. Кроме того, позволяя p находиться в диапазоне меньше нуля и выше 1, мы можем переместить (x2, y2) в любое место вдоль стены:
p = symbols("p")
x0, y0, x1, y1, x2, y2 = symbols("x_0, y_0, x_1, y_1, x_2, y_2")
eq3 = Eq(x2, x0 + (x1-x0) * p)
eq4 = Eq(y2, y0 + (y1-y0) * p)Окружность коснется стены, когда расстояние между ее центральной точкой (x’, y’) и местом на стене, которого она касается (x2, y2), равно радиусу окружности. Другими словами:
eq5 = Eq((x2-aprime_x)**2 + (y2-aprime_y)**2, a_r**2)Однако, когда мы просим SymPy решить и применить эти пять уравнений, это дает нам странные решения, подобные этому:
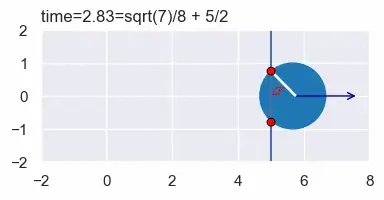
SymPy считает, что это решает наши уравнения, потому что центр круга находится на расстоянии одного радиуса от некоторой точки на стене (две красные точки). Однако это не то решение, которое нам нужно, потому что круг перекрывает стену.
Шестое уравнение может решить проблему. Для этого потребуется, чтобы угол α между стеной и этой белой линией составлял 90° (см. рисунок выше).Мы можем использовать наклоны, чтобы сказать это без явных углов или тригонометрических функций. Наклон стены равен (y1-y0)/(x1-x0). Наклон белой линии на рисунке равен (aprime_y-y2)/(aprime_x-x2). Две линии пересекаются под углом 90°, когда наклон одной из них является отрицательной величиной, обратной другой. В SymPy мы говорим:
slope_0 = (y1-y0)/(x1-x0)
slope_1 = (aprime_y-y2)/(aprime_x-x2)
eq6 = Eq(slope_0, -1/slope_1)Мы просим SymPy решить это для нас следующим образом:
from sympy import nonlinsolve
from perfect_physics import save
cw_all_solutions = nonlinsolve([eq1, eq2, eq3, eq4, eq5, eq6], t, p, aprime_x, aprime_y, x2, y2)
cw_time_solutions = [t for t, p, aprime_x, aprime_y, x2, y2 in cw_all_solutions]
save(cw_time_solutions, "cw_time_solutions.sympy")Проработав 7 минут, он возвращает два решения. Вот первое решение в математической нотации (более читабельное, чем в прошлый раз):
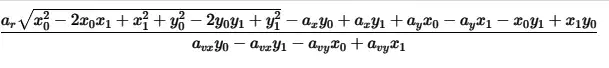
Когда мы применяем эти решения к описанной выше ситуации, Python возвращает временные интервалы [2, 3]:
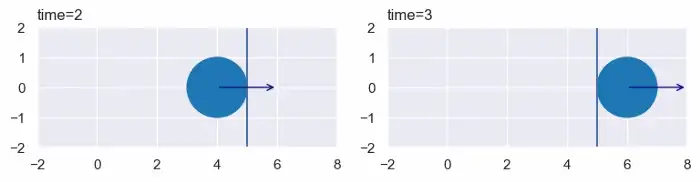
В стороне: выражения решения выглядят как что-то из квадратного уравнения. Это наводит на мысль, что хороший прикладной математик мог бы разобраться в этом вручную. Хорошо для них. Однако, радостно от того, что можно решить проблему с помощью компьютера.
Мы применим те же правила, что и на шаге 1, отфильтровав отрицательные, сложные, nan и сохранив наименьшее время (если таковое имеется). Мы можем столкнуться с одной новой проблемой, когда круг задевает стену:
Этот мир вернется [nan, zoo]. где zoo - это символ SymPy, обозначающий сложную бесконечность. Мы отфильтруем это, потому что нас не волнуют столкновения при выпасе скота.
Давайте добавим этот результат к результату шага 1. Теперь мы можем найти точное, с бесконечной точностью, время следующего «просто касания» между кругом и кругом или стеной.
Далее давайте разберемся, как касание круг-круг может изменить скорость и направление кругов.
Шаг 3: Смоделируем столкновения круг-круг с сохранением импульса и энергии. Добавим «секретное» четвертое уравнение об углах (но не используем углы).
В первый раз, когда мы попытались смоделировать столкновение двух кругов, приходит в голову, что нам понадобятся всего два закона: сохранение импульса и сохранение энергии. но это неправда. Давайте посмотрим, почему.
Закон сохранения энергии гласит, что энергия до и после столкновения должна быть одинаковой. Для наших миров единственным типом энергии является кинетическая, поэтому E= mv²/2, где m - масса, а v - скорость. Мы предположим, что столкновения являются упругими, то есть никакая энергия не преобразуется в тепло, звук и т.д. В математической нотации это становится:
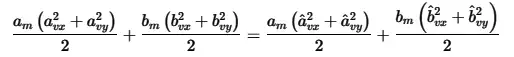
где масса окружности a равна aₘ, ее скорость до столкновения равна (aᵥₓ, aᵥᵧ), а ее скорость после столкновения равна (âᵥₓ, âᵥᵧ). Аналогично для круга b.
В SymPy мы пишем:
from sympy import symbols, Eq
a_x, a_y, a_vx, a_vy, a_r, a_m, ahat_vx, ahat_vy = symbols("a_x, a_y, a_vx, a_vy, a_r, a_m, ahat_vx, ahat_vy")
b_x, b_y, b_vx, b_vy, b_r, b_m, bhat_vx, bhat_vy = symbols("b_x, b_y, b_vx, b_vy, b_r, b_m, bhat_vx, bhat_vy")
energy_before = a_m * (a_vx**2 + a_vy**2) / 2 + b_m * (b_vx**2 + b_vy**2) / 2
energy_after = a_m * (ahat_vx**2 + ahat_vy**2) / 2 + b_m * (bhat_vx**2 + bhat_vy**2) / 2
eq1 = Eq(energy_before, energy_after)Сохранение импульса дает нам еще два уравнения, одно для измерения x и одно для измерения y. Импульс равен массе, умноженной на скорость, так что:
eq2 = Eq(a_m * a_vx + b_m * b_vx, a_m * ahat_vx + b_m * bhat_vx)
eq3 = Eq(a_m * a_vy + b_m * b_vy, a_m * ahat_vy + b_m * bhat_vy)Теперь у нас есть три уравнения, и мы хотим, чтобы SymPy дал нам решения для четырех неизвестных, а именно, скоростей после столкновения: âᵥₓ, âᵥᵧ, b̂ᵥₓ, b̂ᵥᵧ. Это не сработает. Нам нужно столько уравнений, сколько неизвестных.
Тогда мы впервые замечаем это отсутствующее уравнение. В конце концов выясняем четвертый недостающий «закон»:
При столкновении кругов их скорость на 90° от направления столкновения не меняется.
Рассмотрим эту ситуацию:
from perfect_physics import Circle, plot
a = Circle(x=0, y=0, r=1, vx=1, vy=2, m=1)
b = Circle(x=2, y=0, r=1, vx=0, vy=0, m=1)
plot([a, b], colors=["tab:red", "tab:blue"], xlim=(-2, 4), ylim=(-2, 2), figsize=(4, 2), font_scale=1)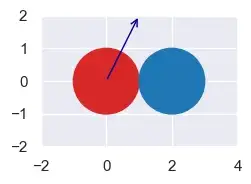
«Направление удара» — это направление от одного центра к другому, здесь горизонтальное. Скорость круга a на 90° от горизонтали равна aᵥᵧ, что равно 2. Таким образом, мы ожидаем, что скорость после столкновения в этом направлении, âᵥᵧ, также будет равна 2.
Но что, если центры окружностей не лежат горизонтально или вертикально? Рассмотрим эту ситуацию:
from sympy import sqrt
from perfect_physics import Circle, plot
a = Circle(x=0, y=0, r=1, vx=1, vy=0, m=1)
b = Circle(x=sqrt(2), y=sqrt(2), r=1, vx=0, vy=0, m=1)
plot([a, b], colors=["tab:red", "tab:blue"], xlim=(-2, 4), ylim=(-2, 3), figsize=(4, 2), font_scale=1)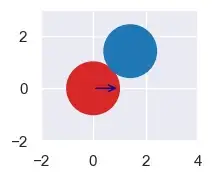
Мы могли бы найти скорость на 90° от направления удара с помощью функции синуса и косинуса. Однако выполнение этого с единичными векторами позволяет нам избежать введения этих функций. Нам нужен вектор <ux,uv> длиной в одну единицу и проходящий под углом 90° от линии между центрами окружностей. Мы можем получить длину, равную единице, разделив на d, расстояние между центрами. Мы можем получить желаемое направление с тем же значением -1/наклон, которое мы использовали на шаге 2. В частности, это говорит о том, что скорость на 90 ° от направления удара не меняется:
from sympy import sqrt
d = sqrt((b_x-a_x)**2 + (b_y-a_y)**2)
ux = -(b_y-a_y)/d
uy = (b_x-a_x)/d
eq4 = Eq((b_vx - a_vx) * ux + (b_vy - a_vy) * uy, (bhat_vx-ahat_vx) * ux + (bhat_vy-ahat_vy) * uy)Мы должны помочь решить наши уравнения:
from sympy import nonlinsolve
from perfect_physics import save
cc_velocity_solutions = nonlinsolve([eq1, eq2, eq3, eq4], ahat_vx, ahat_vy, bhat_vx, bhat_vy)
cc_velocity_solutions = list(cc_velocity_solutions)
save(cc_velocity_solutions[1], "cc_velocity_solution.sympy")Через 2 или 3 минуты он возвращает два решения. Удивительно, но в первом решении говорится, что скорости после равны скоростям до. Другими словами, это решение для случаев, когда круги размыкаются друг с другом.
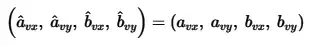
Второе решение, о котором мы заботимся, - длинное.
Давайте применим решение к двум приведенным выше примерам. В первом примере скорости до этого были a.vx=1, a.vy=2, b.vx=0, b.vy=0. После того, как они станут a.vx=0, a.vy=2, b.vx=1, b.vy=0.
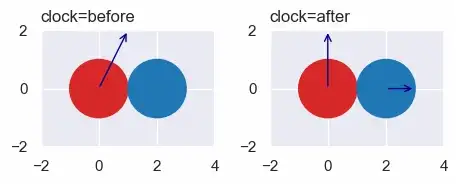
Во втором примере скорости до этого были a.vx=1, a.vy=0, b.vx=0, b.vy=0. После того, как они станут a.vx=1/2, a.vy=-1/2, b.vx=1/2, b.vy=1/2.
Итак, теперь мы можем предсказать, как круги будут отскакивать друг от друга. Позже мы увидим, что это решение работает для окружностей разной массы и разных радиусов.
Затем мы попробуем применить эти законы сохранения к кругам, отскакивающим от стен. Удивительно, но отскок, кажется, нарушает «сохранение импульса».
Шаг 4: Предположим, что стены имеют бесконечную массу. Круг, отскакивающий от стены, нарушает закон сохранения импульса. Исправим это с помощью limit.
Для мяча, отскакивающего от стены, мы могли просто сжульничать. Ответ, который вы, возможно, помните еще со школы, состоит в том, что «угол падения равен углу отражения»:
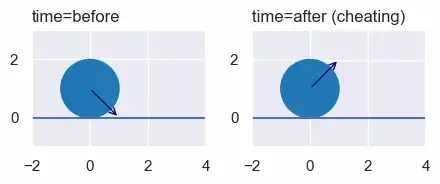
Но как это может быть правильно? y-импульс круга (то есть масса, умноженная на y-скорость) перед отскоком равен -1. После отскока это 1. Это нарушает сохранение импульса. Включение импульса стены не помогает, потому что ее масса бесконечна, а ее y-скорость равна 0, что дает нам неопределенный импульс.
Возможно, мы можем просто смоделировать стены в виде больших кругов и использовать решение из шага 3. Здесь мы придаем большому кругу радиус 20 и массу 1000.
a = Circle(x=0, y=1, r=1, vx=1, vy=-1, m=1)
b = Circle(x=0, y=-20, r=20, vx=0, vy=0, m=1000)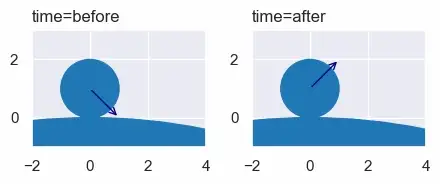
Это почти работает. Последующие скорости: a.vx=1, a.vy=999/1001, b.vx=0, b.vy=-2/1001. Что, если мы вставим бесконечность в качестве массы и/или радиуса большого круга? К сожалению, в результате получаются неопределенные значения.
Давайте посмотрим, сможем ли мы начать с законов сохранения и найти правильный ответ. Мы предположим, что стена имеет конечную массу и скорость 0. Мы учитываем сохранение энергии (eq1), сохранение импульса (eq2, eq3) и то, что относительная скорость круга вдоль стены не должна меняться.
from sympy import symbols, Eq, sqrt
a_x, a_y, a_vx, a_vy, a_r, a_m, ahat_vx, ahat_vy = symbols("a_x, a_y, a_vx, a_vy, a_r, a_m, ahat_vx, ahat_vy")
w_x0, w_y0, w_x1, w_y1, w_m, what_vx, what_vy = symbols("w_x0, w_y0, w_x1, w_y1, w_m, what_vx, what_vy")
energy_before = a_m * (a_vx**2 + a_vy**2) / 2 + w_m * 0
energy_after = a_m * (ahat_vx**2 + ahat_vy**2) / 2 + w_m * (what_vx**2 + what_vy**2) / 2
eq1 = Eq(energy_before, energy_after)
eq2 = Eq(a_m * a_vx + w_m * 0, a_m * ahat_vx + w_m * what_vx)
eq3 = Eq(a_m * a_vy + w_m * 0, a_m * ahat_vy + w_m * what_vy)
d = sqrt((w_x1-w_x0)**2 + (w_y1-w_y0)**2)
ux = (w_x1-w_x0)/d
uy = (w_y1-w_y0)/d
eq4 = Eq(a_vx * ux + a_vy * uy, (ahat_vx-what_vx) * ux + (ahat_vy-what_vy) * uy)Мы снова применяем nonlinsolve и получаем один результат, в котором они не попадают (игнорируются), и второй, в котором они попадают. Наш следующий шаг новый. Мы используем SymPy, чтобы взять предел, когда масса стены стремится к бесконечности.
from sympy import nonlinsolve, limit, oo, Tuple
from perfect_physics import save
no_hit, cw_velocity_solution = nonlinsolve(
[eq1, eq2, eq3, eq4], ahat_vx, ahat_vy, what_vx, what_vy
)
a_vx_limit, a_vy_limit, w_vx_limit, w_vy_limit = [
limit(velocity, w_m, oo) for velocity in cw_velocity_solution
]
assert w_vx_limit == 0 and w_vy_limit == 0
cw_velocity_limits = Tuple(a_vx_limit, a_vy_limit)
save(cw_velocity_limits, "cw_velocity_limits.sympy")Результатом являются значения после vx и vy для круга и стены. Как и ожидалось, скорости стены равны нулю. Мы сохраняем формулы для последующих скоростей окружности.
Когда мы применяем формулу, мы получаем ожидаемый результат «угол падения равен углу отражения»:
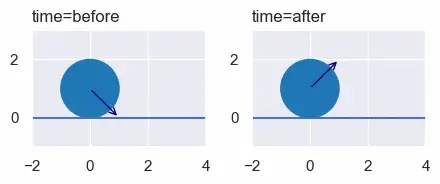
и
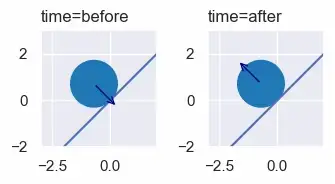
Итак, готовы ли мы теперь решать домашние задания по физике, создавать анимацию и создавать игры? Не совсем. Мы проигнорировали одну проблему: соприкосновение двух объектов не всегда означает, что они сталкиваются.
Шаг 5: Два объекта могут соприкасаться и в то же время удаляться друг от друга. Используем limit, чтобы найти их. Удалим их из списка сталкивающихся объектов.
Как мы определяем, движутся ли два круга навстречу друг другу? Первоначально мы могли бы просто проверить их относительную скорость. Однако относительная скорость красного круга в этих двух ситуациях одинакова. В первом случае они движутся навстречу друг другу, а во втором - нет.
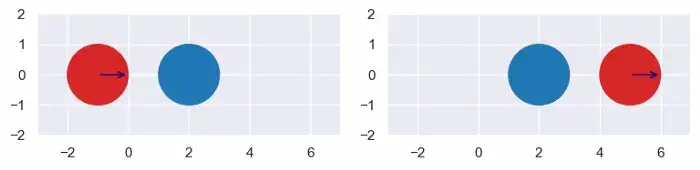
Лучший подход - посмотреть, сближаются ли центры друг с другом. Но когда? Они могут начать с того, что сблизятся, но позже отдалятся друг от друга. Можем ли мы спросить, приближаются ли они к нулевому моменту времени? Это не работает, потому что в любой момент времени их расстояние остается неизменным.
Решение состоит в том, чтобы снова использовать ограничения. Мы проверим, приближаются ли они в момент после нулевого времени.
from sympy import symbols, limit, sqrt
from perfect_physics import save
a_x, a_y, a_vx, a_vy, b_x, b_y, b_vx, b_vy, t = symbols("a_x, a_y, a_vx, a_vy, b_x, b_y, b_vx, b_vy, t")
d0 = sqrt((a_x - b_x) ** 2 + (a_y - b_y) ** 2)
d1 = sqrt((a_x + t * a_vx - (b_x + t * b_vx)) ** 2 + (a_y + t * a_vy - (b_y + t * b_vy)) ** 2)
speed_toward = (d0 - d1) / t
instant_speed = limit(speed_toward, t, 0)
save(instant_speed, "instant_speed.sympy")В первом примере выше применение результирующей формулы возвращает 1. Во втором примере он возвращает значение -1. Оба результата соответствуют ожиданиям.
Чтобы увидеть, движется ли круг к стене, мы находим (x₂, y₂), точку на стене, в которую может попасть центр круга. Для этого требуются четыре уравнения, которые могут быть решены с помощью SymPy linsolve. Затем мы используем формулу instant_speed, которую мы только что нашли, чтобы увидеть, как быстро круг движется к этой точке или от нее:
from sympy import symbols, linsolve, Eq, simplify
from perfect_physics import load, save
a_x, a_y, a_vx, a_vy, t = symbols("a_x, a_y, a_vx, a_vy, t")
x0, y0, x1, y1, x2, y2, p = symbols("x_0, y_0, x_1, y_1, x_2, y_2, p")
eq1 = Eq(x2, a_x + a_vx * t)
eq2 = Eq(y2, a_y + a_vy * t)
eq3 = Eq(x2, x0 + (x1-x0) * p)
eq4 = Eq(y2, y0 + (y1-y0) * p)
x2_formula, y2_formula, _, _ = list(linsolve([eq1, eq2, eq3, eq4], (x2, y2, p, t)))[0]
instant_speed = load("instant_speed.sympy")
instant_speed_wall = simplify(instant_speed.subs({"b_x": x2_formula, "b_y": y2_formula, "b_vx": 0, "b_vy": 0}))
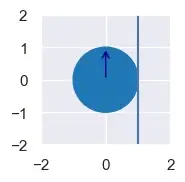
save(instant_speed_wall, "instant_speed_wall.sympy")Например, для этой ситуации мы обнаруживаем, что круг движется к стене со скоростью sqrt(5).
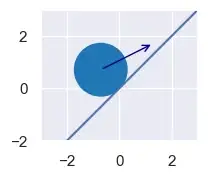
from sympy import sqrt
from perfect_physics import Circle, Wall, plot, load
a = Circle(x=-sqrt(2) / 2, y=sqrt(2) / 2, r=1, vx=2, vy=1)
w = Wall(x0=-1, y0=-1, x1=1, y1=1)
plot(circle_list=[a], wall_list=[w], xlim=(-3, 3), ylim=(-2, 3), figsize=(4, 2), font_scale=1)
instant_speed_wall = load("instant_speed_wall.sympy")
instant_speed_wall.subs({"a_x": a.x, "a_y": a.y, "a_vx": a.vx, "a_vy": a.vy,
"x_0": w.x0, "y_0": w.y0, "x_1": w.x1, "y_1": w.y1})Теперь у нас есть все необходимое для создания физического движка с бесконечной точностью.
Подводим итоги
В этой части мы рассмотрели, как использовать пакет Python SymPy для поиска низкоуровневых выражений, необходимых для создания идеального физического движка для наших 2-D миров circles и wall. Мы нашли выражения для времени, когда два объекта просто соприкоснутся (если они когда-либо соприкоснутся). Когда они соприкасаются, мы нашли выражения для их новых скоростей.
Изучив детали, мы увидели:
- Инженерные уравнения относительно просты, но вручную решать системы нелинейных уравнений было бы сложно. К счастью, компьютер выполняет эту тяжелую работу за нас.
- Сохранения энергии и импульса недостаточно для прогнозирования скоростей после столкновения. Нам нужно четвертое уравнение, в котором говорится, что скорость на 90° от столкновения не меняется.
- Наши уравнения часто дают странные ответы. Мы видели ответы с
nan, отрицательными временными интервалами, комплексными числами и комплексной бесконечностью. Мы интерпретируем эти странные ответы, а затем обрабатываем их. Например, отрицательный временной интервал означает, что столкновение произошло в прошлом и, следовательно, может быть проигнорировано. - Дважды нам требовались углы 90°. В обоих случаях мы избегаем введения синуса, косинуса и т.д., Используя наклоны и единичные векторы.
- Когда-то нам нужно было бесконечно малое время, а когда-то нам нужна была бесконечная масса. В обоих случаях функция SymPy
limitпозволяет нам использовать необходимое нам экстремальное время и массу.
Теперь мы создали низкоуровневые выражения, которые обеспечивают основу, необходимую нам для высокоуровневого слоя. Когда мы соединяем оба слоя вместе, мы получаем идеальный физический движок. Однако это будет мучительно медленно.
Теперь мы создали низкоуровневые выражения, которые обеспечивают основу, необходимую для высокоуровневого уровня. Мы видели высокоуровневый слой в серии 1 и серии 2. Когда мы соединяем оба слоя вместе, мы получаем идеальный физический движок.