Создайте двухслойную нейронную сеть с нуля

В этой статье представлена разработка двухслойной нейронной сети (НС) только с использованием NumPy. Этот проект представляет собой практическое введение в основы глубокого обучения и архитектуры нейронных сетей. Основное внимание будет уделено поэтапному построению сети с целью обеспечить четкое и простое понимание ее базовой механики (математики, лежащей в основе НС).
Почему двухслойная нейронная сеть?
В выборе двух слоев нет никакого секрета. В этом проекте мы будем экспериментировать с различными вариантами гиперпараметров НС; следовательно, двухуровневая архитектура достаточно проста, чтобы сделать тест осуществимым.
Моделирование данных
Прежде всего, мы моделируем некоторые данные, используя наборы данных из пакета Scikit-learn.
from utils_data import *
N = 2000
noise = 0.25
# load and visualize data
X, Y = load_data(N, noise)
# visualize the data
path_to_save_plot = os.path.join("input", "viz")
plot_data(X, Y, path_to_save_plot)
Наш набор данных состоит из двух категорий, представленных красными и синими точками. Если вам нравится думать о реальной проблеме, синий цвет может представлять мужчин, а красный — женщин в выборке.
Цель состоит в том, чтобы разработать модель, которая точно различает красные и синие группы. Проблема здесь в том, что данные не являются линейно разделимыми, другими словами, вероятно, будет сложно провести прямую линию, которая четко разделит две группы. Это ограничение означает, что линейные модели (например, логистическая регрессия) вряд ли будут эффективными. Этот сценарий подчеркивает одну из ключевых сильных сторон нейронных сетей: их способность эффективно обрабатывать данные, которые не поддаются линейному разделению.
Общая форма нейронной сети
Нейронная сеть состоит из слоев взаимосвязанных узлов (или «нейронов»). Эти слои включают в себя:
- Входной уровень: здесь сеть получает входные данные.
- Скрытые слои: эти слои, которых может быть один или несколько, выполняют вычисления над входными данными. Каждый нейрон в этих слоях применяет к данным две математические функции.
- Выходной уровень: этот уровень формирует конечный результат работы сети, такой как классификация (например, определение принадлежности точки данных к красной или синей группам) или непрерывное значение (например, прогнозирование цен на жилье).
Как нейронная сеть делает прогнозы
В этом примере двухслойной нейронной сети данные передаются из входного слоя, подвергаются вычислениям в скрытых слоях, а выходной уровень генерирует результат. Математически НС генерирует вероятность, которая определяет принадлежность прогноза результата к группе 0 или 1. Вычисление можно записать следующим образом:
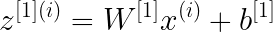
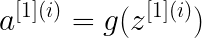
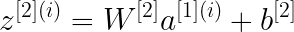
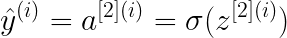
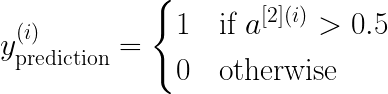
В этом проекте будут рассмотрены три варианта функции активации: sigmoid, tanh и relu.
# define helper functions in utils_1batch.py
# ________________ sigmoid function ________________ #
def sigmoid(x):
s = 1 / (1 + np.exp(-x))
return s
# ________________ relu function ________________ #
def relu(x):
return np.maximum(0, x)Мы использовали tanh() из пакета NumPy.
Затем нам нужен способ инициализировать параметры и вычислить прямое распространение в коде Python следующим образом:
# ________________ initialize parameters ________________ #
def initialize_parameters(n_x, n_h, n_y):
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2}
return parameters
# ________________ compute forward propagation ________________ #
def forward_propagation(X, parameters, activation):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1, X) + b1
# there are 3 options for the function g()
if activation == "tanh":
A1 = np.tanh(Z1)
elif activation == "sigmoid":
A1 = sigmoid(Z1)
elif activation == "relu":
A1 = relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
# store values for the back_propagation usage later
temp_cache = {
"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2,
}
return A2, temp_cacheКак учится нейронная сеть
Обучение нашей нейронной сети включает в себя определение оптимальных параметров (W1, b1, W2, b2), которые минимизируют расхождение между прогнозом и истинной истиной. Ключевой вопрос заключается в том, как количественно оценить это несоответствие или ошибку. Чтобы оценить эту ошибку, мы используем так называемую функцию стоимости J() следующим образом:
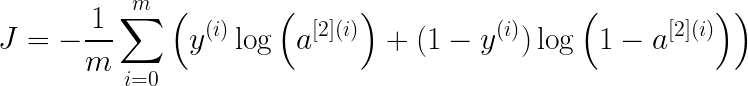
# define helper functions in utils_1batch.py
def compute_cost(A2, Y):
# get the number of examples
m = Y.shape[1]
# compute the loss function
logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1 - A2), (1 - Y))
# sum of loss funtions = the cost function
cost = -np.sum(logprobs) / m
cost = float(np.squeeze(cost))
return costКак только стоимость будет рассчитана, целью будет минимизация затрат. Другими словами, мы ищем решение, которое минимизирует расхождение между предсказанием и истиной (максимизирует вероятность). Именно здесь на помощь приходит градиентный спуск. В этом проекте мы реализуем упрощенную версию алгоритма градиентного спуска (применяем градиентный спуск ко всему пакету данных с одной фиксированной скоростью обучения).
Чтобы градиентный спуск работал, ему нужны градиенты (вектор производных), относящиеся к следующим параметрам:

Расчет этих градиентов осуществляется с помощью алгоритма обратного распространения ошибки — эффективного метода, который начинается с выходных данных и идет в обратном направлении для определения градиентов. Параметры обновляются одновременно до тех пор, пока не будет определена минимальная стоимость.
# define helper functions in utils_1batch.py
# ________________ compute back propagation ________________ #
def backward_propagation(parameters, temp_cache, X, Y, activation):
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = temp_cache["A1"]
A2 = temp_cache["A2"]
# compute the backward_propagation
dZ2 = A2 - Y
dW2 = np.dot(dZ2, A1.T) / m
db2 = np.sum(dZ2, axis=1, keepdims=True) / m
if activation == "tanh":
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2)) # derivative of tanh
elif activation == "sigmoid":
dZ1 = np.dot(W2.T, dZ2) * (A1 * (1 - A1)) # derivative of sigmoid
elif activation == "relu":
dZ1 = np.dot(W2.T, dZ2) * relu_derivative(A1) # derivative of ReLU
dW1 = np.dot(dZ1, X.T) / m
db1 = np.sum(dZ1, axis=1, keepdims=True) / m
gradients = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}
return gradients
# ________________ update the parameters ________________ #
def update_parameters(parameters, grads, learning_rate):
# retrieve the parameters from the input
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# retrieve the gradient from the input
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
# update the parameters after comparing
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
}
return parametersОбъедините все вместе, чтобы создать двухслойную НС следующим образом:
# define helper functions in utils_1batch.py
def nn_1layer_1batch(
X, Y, n_h, learning_rate, activation, number_iterations, print_cost=False
):
# set up
np.random.seed(0)
n_x = X.shape[0]
n_y = Y.shape[0]
# initialize parameters
parameters = initialize_parameters(n_x, n_h, n_y)
# initialize cost array
costs = np.zeros(number_iterations)
# Loop through forward and backward propagations
for i in range(0, number_iterations):
# apply forward_propagation
A2, temp_cache = forward_propagation(X, parameters, activation)
# compute the cost
cost = compute_cost(A2, Y)
# save the cost
costs[i] = cost
# apply backward_propagation
grads = backward_propagation(parameters, temp_cache, X, Y, activation)
# gradient descent parameter updats
parameters = update_parameters(parameters, grads, learning_rate=learning_rate)
# print the cost after every 1000 loops
if print_cost and i % 1000 == 0:
print("Cost after interation %i: %f" % (i, cost))
return parameters, costsТестируйте различные конфигурации модели
Часто задаваемый вопрос новичками при изучении НС: какие гиперпараметры оптимальнее использовать? Довольно простая архитектура, подобная этой двухуровневой нейронной сети, позволяет экспериментировать с несколькими вариантами гиперпараметров.
from utils_1batch import *
# number of features
n_x = 2
# the number of nodes in the hidden layer
n_hs = np.array([1, 2, 3, 4, 5, 10, 50])
# choice of activation funtion
activations = np.array(["tanh", "sigmoid", "relu"])
# learning rate
learning_rates = np.array([1.2, 0.6, 0.1, 0.01, 0.001])
# number of iterations
number_iterations = np.array([100, 1000, 10000, 100000])
def run_test_1batch():
# run the test
test_nodes_1batch(
file_name,
data,
n_hs,
number_iterations=number_iterations,
learning_rates=learning_rates,
activations=activations,
batch_type="one batch",
)
Важнейшим компонентом является изучение того, как каждая конфигурация работает с обучающими и тестовыми наборами данных. Мы применим приведенные ниже функции для расчета точности.
# ________________ make predictions using the NN ________________ #
def predict(X, parameters, activation):
X = X.T
A2, temp_cache = forward_propagation(X, parameters, activation)
predictions = (A2 > 0.5).astype(int)
return predictions
# ________________ compute the accuracy of the NN ________________ #
def compute_accuracy(Y, Y_hat):
accuracy = float(
(np.dot(Y, Y_hat.T) + np.dot(1 - Y, 1 - Y_hat.T)) / float(Y.size) * 100
)
accuracy = round(accuracy, 2)
return accuracyИзучение результатов
Визуализация показывает широкий спектр результатов при использовании разных конфигураций одной и той же архитектуры нейронной сети для решения одной и той же проблемы. Некоторые конфигурации выделяются, достигая высокого уровня точности выше 90%, и в этой группе есть исключительные случаи, когда точность превышает 95%. Эти высокопроизводительные конфигурации являются главными кандидатами для дальнейшего изучения. Следующим аналитическим шагом будет отфильтровать конфигурации с точностью более 95% и провести более целенаправленное сравнение наборов данных обучения и разработки.
Обычной практикой при разработке моделей является то, что мы не хотим проблем с переоснащением, когда модель хорошо работает в наборе обучающих данных, но плохо подходит для набора данных разработки. Поэтому удаляем конфигурации, отвечающие двум условиям:
- Точность > 95%
- Разница между наборами данных обучения и развития составляет > 1%.
Разница в 1% субъективна, однако в этом упражнении она достаточна хороша.
После фильтрации у нас осталось несколько конфигураций. Следующим шагом будет рассмотрение того, сколько времени занимает обучение каждой конфигурации.
Из диаграммы рассеяния мы можем наблюдать значительные различия во времени обучения для разных конфигураций. Несмотря на то, что производительность модели по степени соответствия очень схожа, некоторые конфигурации требуют большого количества ресурсов обучения, в то время как другие можно обучить очень быстро. При решении реальных задач, вероятно, предпочтительнее те, которые требуют меньше ресурсов. Теперь я отфильтрую конфигурации со временем обучения < 30 секунд. Таким образом, после фильтрации сохраняются два кандидата.

Глядя на двух кандидатов, я выберу того, которому требуется наименьшее время обучения. Наконец, в этом эксперименте я опробую выбранную конфигурацию на новом наборе данных моделирования, чтобы увидеть, как она работает на совершенно новых данных.
Моделирование данных:
N = 500
noise = 0.25
# load and visualize data
X, Y = load_data(N, noise)
X = X.T
Y = Y.reshape(1, Y.shape[0])
Тестирование на вновь смоделированных данных:
import pickle
with open('../output/data/parameters/parameters_3_tanh_one batch_0.6_10000.pkl', 'rb') as file:
parameters = pickle.load(file)
Y_hat = predict(X.T, parameters, "tanh")
accuracy = compute_accuracy(Y, Y_hat)
print(f"Accuracy: {accuracy} % ")
Точность: 93,6%
Все шаги, представленные в этом разделе результатов исследования, можно найти в файле EDA.ipynb.
Подводя итог, отметим, что эта двухслойная нейронная сеть не решит никаких реальных задач, но является отличной отправной точкой для тех, кто погружается в искусственный интеллект, машинное обучение и глубокое обучение. Часто для решения реальных задач вы будете использовать известные библиотеки. Этот эксперимент может прояснить туман о том, что происходит под капотом. Важно осознавать, что это лишь верхушка айсберга во вселенной глубокого обучения, которая включает в себя такие продвинутые концепции, как мини-пакеты, снижение скорости обучения и многое другое.