Внедрение дерева решений с нуля
Деревья решений просты и легко объяснимы. Они могут быть легко отображены графически и следовательно, допускают гораздо более простую интерпретацию. Они также являются довольно популярным и успешным оружием, когда речь идет о соревнованиях по машинному обучению (например Kaggle).
Однако простота на первый взгляд не означает, что алгоритм и лежащие в его основе механизмы скучны или даже тривиальны.
В следующих разделах мы собираемся поэтапно реализовать дерево решений для классификации, используя только Python и NumPy. Мы также узнаем о концепциях энтропии и получения информации, которые дают нам средства для оценки возможных расщеплений, что позволяет нам разумно вырастить дерево решений.
Но прежде чем погрузиться непосредственно в детали реализации, давайте установим некоторые базовые интуитивные представления о деревьях решений в целом.
Деревья решений 101: Дендрология
Методы на основе дерева просты и полезны для интерпретации, поскольку лежащие в их основе механизмы считаются очень похожими на процесс принятия решений человеком.
Методы включают стратификацию или сегментацию пространства предикторов на несколько более простых областей. Делая прогноз, мы просто используем среднее значение или режим области, к которой принадлежит новое наблюдение, в качестве значения отклика.
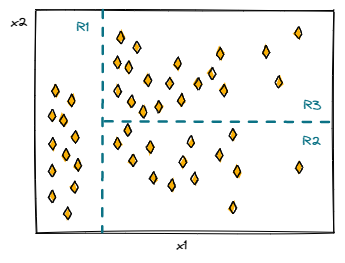
Поскольку правила разделения для сегментирования пространства предикторов лучше всего могут быть описаны древовидной структурой, алгоритм обучения с учителем называется деревом решений.
Деревья решений можно использовать как для задач регрессии, так и для задач классификации.
Теперь, когда мы знаем, что такое дерево решений и почему оно может быть полезным, нам нужно знать, как его вырастить?
Посадка семени: как вырастить дерево решений
Грубо говоря, процесс построения дерева решений в основном состоит из двух этапов:
- Разделение пространства предикторов на несколько отдельных непересекающихся областей
- Прогнозирование наиболее распространенной метки класса для области, к которой принадлежит любое новое наблюдение
Как бы просто это ни звучало, возникает один фундаментальный вопрос — как разделить пространство предикторов?
Чтобы разделить пространство предикторов на отдельные области, мы используем бинарное рекурсивное разбиение, которое увеличивает наше дерево решений до тех пор, пока мы не достигнем критерия остановки. Поскольку нам нужен разумный способ решить, какие разбиения полезны, а какие нет, нам также нужна метрика для целей оценки.
В теории информации энтропия описывает средний уровень информации или неопределенности и может быть определена следующим образом:
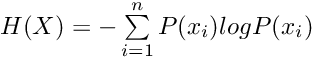
Мы можем использовать концепцию энтропии для расчета прироста информации в результате возможного разделения.
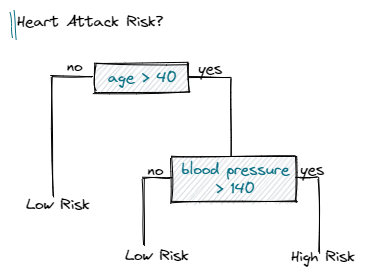
Предположим, у нас есть набор данных, содержащий разные данные о пациентах. Теперь мы хотим классифицировать каждого пациента как имеющего высокий или низкий риск сердечного приступа. Представьте себе возможное дерево решений, подобное следующему:
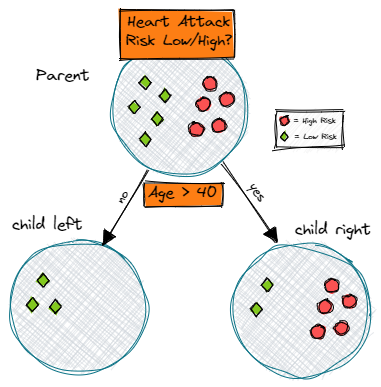
Чтобы рассчитать прирост информации разделения (IG), мы просто вычисляем сумму взвешенных энтропий дочерних элементов и вычитаем ее из энтропии родителя.
Давайте проработаем наш пример, чтобы прояснить ситуацию:
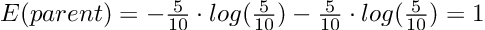
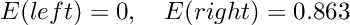
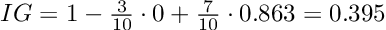
Прирост информации, равный 1, был бы наилучшим возможным результатом. Однако в нашем примере расщепление дает информационный прирост примерно 0,395 и следовательно, содержит гораздо больше неопределенности или другими словами, более высокое значение энтропии.
Вооружившись понятиями энтропии и прироста информации, нам просто нужно оценить все возможные разбиения на текущем этапе роста дерева (жадный подход), выбрать лучший и продолжать рекурсивно расти, пока не достигнем критерия остановки.
Знакомство с алгоритмом
Теперь, когда мы рассмотрели все основы, мы можем приступить к реализации алгоритма обучения.
Но прежде чем углубиться непосредственно в детали реализации, мы кратко рассмотрим основные вычислительные этапы алгоритма, чтобы предоставить общий обзор, а также некоторую базовую структуру.
Основной алгоритм можно условно разделить на три шага:
- Инициализация параметров (например, максимальная глубина, минимальное количество выборок на разделение) и создание вспомогательного класса
- Построение дерева решений, включающее бинарное рекурсивное разбиение, оценку каждого возможного разбиения на текущем этапе и продолжение роста дерева до тех пор, пока не будет удовлетворен критерий остановки.
- Создание прогноза, который можно описать как рекурсивный обход дерева и возврат наиболее распространенной метки класса в качестве значения ответа.
Поскольку построение дерева состоит из нескольких шагов, мы будем в значительной степени полагаться на использование вспомогательных функций, чтобы сделать наш код как можно более чистым.
Алгоритм будет реализован в двух классах: основной класс, содержащий сам алгоритм, и вспомогательный класс, определяющий узел. Ниже мы можем взглянуть на скелетные классы, которые можно интерпретировать как своего рода план, помогающий нам в реализации в следующем разделе.
class Node:
def __init__(self, feature=None, threshold=None, left=None, right=None, *, value=None):
pass
def is_leaf(self):
passclass DecisionTree:
def __init__(self, max_depth=100, min_samples_split=2):
pass
def _is_finished(self, depth):
pass
def _entropy(self, y):
pass
def _create_split(self, X, thresh):
pass
def _information_gain(self, X, y, thresh):
pass
def _best_split(self, X, y, features):
pass
def _build_tree(self, X, y, depth=0):
pass
def _traverse_tree(self, x, node):
pass
def fit(self, X, y):
pass
def predict(self, X):
pass
Внедрение с нуля
Базовая установка и узел
Давайте начнем нашу реализацию с некоторой базовой уборки. Прежде всего, мы определяем некоторые основные параметры для нашего основного класса, а именно критерии остановки max_depth, min_samples_split и root node.
class DecisionTree:
def __init__(self, max_depth=100, min_samples_split=2):
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.root = None
Затем мы определяем небольшой вспомогательный класс, который хранит наши разбиения в узле. Узел содержит информацию о feature, threshold значении, подключенном left и right дочернем элементе, которая будет полезна, когда мы рекурсивно проходим по дереву, чтобы сделать прогноз.
class Node:
def __init__(self, feature=None, threshold=None, left=None, right=None, *, value=None):
self.feature = feature
self.threshold = threshold
self.left = left
self.right = right
self.value = value
def is_leaf(self):
return self.value is not None
Построение дерева
Теперь все становится немного сложнее. Таким образом, в дальнейшем мы будем в значительной степени полагаться на использование нескольких вспомогательных методов, чтобы оставаться организованными.
class DecisionTree:
def _is_finished(self, depth):
if (depth >= self.max_depth
or self.n_class_labels == 1
or self.n_samples < self.min_samples_split):
return True
return False
def _build_tree(self, X, y, depth=0):
self.n_samples, self.n_features = X.shape
self.n_class_labels = len(np.unique(y))
# stopping criteria
if self._is_finished(depth):
most_common_Label = np.argmax(np.bincount(y))
return Node(value=most_common_Label)
def fit(self, X, y):
self.root = self._build_tree(X, y)
#...
Мы начинаем процесс построения с вызова метода fit(), который просто вызывает наш основной метод _build_tree().
В основном методе мы просто собираем некоторую информацию о наборе данных (количество выборок, признаков и уникальных меток классов), которая потребуется, чтобы решить, соблюдены ли критерии остановки.
Наш вспомогательный метод _is_finished() используется для оценки критериев остановки. Если, например, осталось меньше выборок, чем минимально необходимое количество выборок на оставшееся разделение, наш метод возвращается True, и процесс построения будет остановлен в этой текущей ветви.
Если наш процесс сборки завершен, мы вычисляем наиболее распространенную метку класса и сохраняем это значение в файле leaf node.
Примечание. Критерий остановки служит стратегией выхода для остановки рекурсивного роста. Без стопорного механизма мы бы создали бесконечный цикл.
class DecisionTree:
#...
def _entropy(self, y):
proportions = np.bincount(y) / len(y)
entropy = -np.sum([p * np.log2(p) for p in proportions if p > 0])
return entropy
def _create_split(self, X, thresh):
left_idx = np.argwhere(X <= thresh).flatten()
right_idx = np.argwhere(X > thresh).flatten()
return left_idx, right_idx
def _information_gain(self, X, y, thresh):
parent_loss = self._entropy(y)
left_idx, right_idx = self._create_split(X, thresh)
n, n_left, n_right = len(y), len(left_idx), len(right_idx)
if n_left == 0 or n_right == 0:
return 0
child_loss = (n_left / n) * self._entropy(y[left_idx]) + (n_right / n) * self._entropy(y[right_idx])
return parent_loss - child_loss
def _best_split(self, X, y, features):
split = {'score':- 1, 'feat': None, 'thresh': None}
for feat in features:
X_feat = X[:, feat]
thresholds = np.unique(X_feat)
for thresh in thresholds:
score = self._information_gain(X_feat, y, thresh)
if score > split['score']:
split['score'] = score
split['feat'] = feat
split['thresh'] = thresh
return split['feat'], split['thresh']
def _build_tree(self, X, y, depth=0):
#...
# get best split
rnd_feats = np.random.choice(self.n_features, self.n_features, replace=False)
best_feat, best_thresh = self._best_split(X, y, rnd_feats)Мы продолжаем расширять наше дерево, вычисляя лучшее разделение на текущем этапе. Чтобы получить наилучшее разделение, мы перебираем все индексы функций и уникальные пороговые значения для расчета прироста информации. В предыдущих разделах мы уже узнали, как рассчитать прирост информации, который в основном говорит нам, сколько неопределенности может быть устранено предлагаемым разделением.
Как только мы получим прирост информации для конкретной комбинации признаков и порогов, мы сравним результат с нашими предыдущими итерациями. Если мы находим лучшее разделение, мы сохраняем связанные параметры в словаре.
После перебора всех комбинаций мы возвращаем лучший признак и порог в виде кортежа.
class DecisionTree:
#...
def _build_tree(self, X, y, depth=0):
#...
# grow children recursively
left_idx, right_idx = self._create_split(X[:, best_feat], best_thresh)
left_child = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)
right_child = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)
return Node(best_feat, best_thresh, left_child, right_child)
Теперь мы можем закончить наш основной метод, рекурсивно вырастив дочерние элементы. Поэтому мы разделяем данные, используя лучшую функцию и пороговое значение, на левую и правую ветви.
Затем мы вызываем наш основной метод из самого себя (здесь это рекурсивная часть), чтобы начать процесс построения дочерних элементов.
Как только мы удовлетворяем критериям остановки, метод будет рекурсивно возвращать все узлы, что позволит нам построить полноценное дерево решений.
Предсказание — или обход дерева
Мы закончили большую часть тяжелой работы — нам просто нужно создать еще один вспомогательный метод, и все готово.
class DecisionTree:
#...
def _traverse_tree(self, x, node):
if node.is_leaf():
return node.value
if x[node.feature] <= node.threshold:
return self._traverse_tree(x, node.left)
return self._traverse_tree(x, node.right)
def predict(self, X):
predictions = [self._traverse_tree(x, self.root) for x in X]
return np.array(predictions)Предсказание можно реализовать путем рекурсивного обхода дерева. Это означает, что для каждой выборки в нашем наборе данных мы сравниваем функцию узла и пороговые значения со значениями текущей выборки и решаем, нужно ли нам повернуть налево или направо.
Как только мы достигаем конечного узла, мы просто возвращаем наиболее распространенную метку класса в качестве нашего прогноза.
И это он! Мы закончили реализацию дерева решений.
Тестирование классификатора
Закончив реализацию, нам еще нужно протестировать наш классификатор.
В целях тестирования мы будем использовать набор данных Висконсина с классической бинарной классификацией рака молочной железы. Всего набор данных содержит 30 измерений и 569 выборок.
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from DecisionTree import DecisionTree
def accuracy(y_true, y_pred):
accuracy = np.sum(y_true == y_pred) / len(y_true)
return accuracy
data = datasets.load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1
)
clf = DecisionTree(max_depth=10)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
acc = accuracy(y_test, y_pred)
print("Accuracy:", acc)
После импорта набора данных мы можем разделить его на обучающую и тестовую выборки соответственно.
Мы создаем экземпляр нашего классификатора, подгоняем его к обучающим данным и делаем наши прогнозы. Используя нашу вспомогательную функцию, мы получаем точность ~ 95,6%, что позволяет нам подтвердить, что наш алгоритм работает.