Анализ решений и деревья в Python

Использование деревьев решений в Python для получения информации о решении A переехать в Лас-Вегас.
Совсем недавно владелец бейсбольной команды Oakland Athletics Джон Фишер объявил, что команда приобрела около 50 акров земли в Лас-Вегасе, штат Невада.[1] Это ставит под угрозу будущее последней оставшейся профессиональной спортивной команды Окленда. За последние 5 лет в Окленде «Голден Стэйт Уорриорз» (НБА) и «Лас-Вегас Рейдерс» (НФЛ) отправились на более новые, более блестящие стадионы в других городах (хотя «Голден Стэйт» только что пересек мост через залив в Сан-Франциско). Хотя процесс принятия решений во фронт-офисе Oakland A остается для меня загадкой, наука о данных и анализ решений в тандеме могут многое рассказать о мотивах Джона Фишера переехать в Лас-Вегас.
Анализ решений важен для понимания всеми учеными, занимающимися данными, потому что он является мостом между высокотехнологичной работой вероятностных и статистических моделей и бизнес-решениями. Понимание того, как принимаются бизнес-решения, может помочь сформулировать нашу работу и представить наши выводы нетехнической аудитории, поскольку мы предоставляем действенные рекомендации и выводы. В Институте исследования операций и управления (INFORMS) даже есть целое общество, занимающееся анализом решений.
Кроме того, машинное обучение может помочь обобщить результаты анализа решений, открывая возможности вероятностного анализа чувствительности. После первоначального построения модели, анализирующей сценарии Окленда и Лас-Вегаса с использованием анализа решений, мы будем использовать машинное обучение для поиска шаблонов, которые могут помочь выявить действенные рекомендации для А, если обстоятельства принятия решения изменятся.
Что такое анализ решений?
Анализ решений — это область исследования, посвященная «систематическому, количественному и визуальному подходу к рассмотрению и оценке важных вариантов».[2] Это может быть мощным инструментом в среде с низким объемом данных и помочь людям использовать сочетание экспертных знаний в предметной области и предварительных знаний для повышения ожидаемой ценности сложных решений. Он используется в самых разных областях, таких как экономика, управление и анализ политики.
Как правило, в мире анализа решений мы принимаем байесовскую точку зрения на мир. Основная теорема Байеса заключается в следующем:
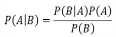
Где: P(A) — вероятность возникновения события A, P(B) — вероятность возникновения события B, P(A|B) — вероятность возникновения события A при условии, что событие B произошло, а P(B|A) — вероятность наступления события B при условии, что произошло событие A. Как правило, P(A) представляет собой априорное мнение о вероятности наступления события A, а B представляет некоторые новые данные. P(A|B) — это обновленное апостериорное убеждение о вероятности наступления события A после того, как вы наблюдали событие B.
Например, предположим, что мы идем в Колизей округа Окленд-Аламеда, чтобы посмотреть игру в мяч, но мы не отслеживаем статистику игроков. Мы начинаем со знания, что аутфилдеры попадают на базу с вероятностью 0,35, инфилдеры попадают на базу с вероятностью 0,25, а назначенные нападающие попадают на базу с вероятностью 0,4. Пусть A будет событием, что следующий отбивающий будет аутфилдером, B будет событием, что следующий отбивающий станет инфилдером, а C будет событием, что следующий отбивающий станет назначенным нападающим. Поскольку нам известен состав бейсбольной команды, мы уже знаем, что P(A) = 0,33, P(B) = 0,56 и P(C) = 0,11. Теперь следующий отбивающий подходит к тарелке и, к нашей радости, попадает на базу (событие D)! Из наших предыдущих знаний о бейсболе мы знаем, что P(D|A) = 0,35, P(D|B) = 0,25 и P(D|C) = 0,4. Используя закон полной вероятности, мы можем вычислить P(D) = P(D|A)P(A) + P(D|B)P(D) + P(D|C)P(C) = 0,3. Теперь мы можем обновить наши представления о том, каким игроком был отбивающий: P(A|D) = 0,39, P(B|D) = 0,47 и P(C|D) = 0,15. Увидев, как игрок попадает на базу, мы теперь с большей вероятностью поверим, что игрок не был инфилдером. Теперь, когда вы находитесь в правильном настроении, давайте продолжим.
Ключевым инструментом анализа решений является дерево решений (не путать с одноименным алгоритмом машинного обучения).[3] Дерево решений состоит из двух основных компонентов: узла решения и узла выбора.[3] В этом блоге я собираюсь показать вам, как построить дерево решений, оценить его в Python и понять решение Окленда А переехать в Лас-Вегас.
Какое решение?
Ховард и Аббас определяют решение как «выбор между двумя или более альтернативами, который предполагает безвозвратное распределение ресурсов».[3] Это широкое определение, но в нашем примере с командой «А» из Окленда решение таково: должна ли бейсбольная команда «Атлетикс» остаться в Окленде или переехать в Лас-Вегас? В этом случае решение бесповоротно, потому что новый стадион будут строить вне зависимости от выбранного города.
Какие неопределенности?
Неопределенность окружает каждое решение, которое мы принимаем. Принимая решение о том, оставаться ли в Окленде или переезжать в Лас-Вегас, члены А не уверены в стоимости нового стадиона и последующих операционных доходах: 1) сколько государственных денег они получат для финансирования своего нового стадиона, 2) какой доход они получат. приносят от продажи билетов, и 3) какой доход они принесут от сделок с местным телевидением.
В настоящее время «А» надеются построить в Лас-Вегасе стадион стоимостью 1,5 миллиарда долларов. [1] Еще в 2021 году организация запросила 855 миллионов долларов из государственных денег, чтобы помочь построить их новый стадион в Окленде, несмотря на то, что ранее было согласовано с городом и округом, что новый стадион в Окленде будет финансироваться из частных источников. [1] Таким образом, можно обоснованно предположить, что стоимость строительства стадиона примерно одинакова в обоих населенных пунктах. Единственная неопределенность здесь заключается в том, сколько денег налогоплательщиков пойдет на финансирование стадиона.
Предполагаемый доход от продажи билетов сильно различается между командами: от 27 до 131 миллиона долларов при медиане около 75 миллионов долларов. [4] По оценкам, доход Окленда от продажи билетов составил около 55 миллионов долларов. [4]
Доходы от телевидения в MLB равномерно распределяются по сделкам с национальным телевидением, заключаемым MLB. Однако важная составляющая доходов от телетрансляций отдельных команд поступает через региональные спортивные сети (RSN). Команды получают большую часть доходов от сделок с местным телевидением, хотя по-прежнему существует значительная часть доходов. После распределения доходов доходы от телевизионных контрактов с RSN варьировались от 36 до 131 миллиона долларов, при этом все команды, кроме самых ценных, зарабатывали менее 60 миллионов долларов. [4]
Благодаря переезду Raiders (NFL) в Лас-Вегас из Окленда несколько лет назад, мы знаем, что город Лас-Вегас был готов выделить 750 миллионов долларов из государственных средств на строительство совершенно нового футбольного стадиона. [5] Мы также знаем, что и местные жители, и туристы готовы присоединиться и поддержать новую профессиональную команду, поскольку «Рейдеры» возглавили НФЛ по доходам от билетов в 2021 году, составив 119 миллионов долларов за год. [6]
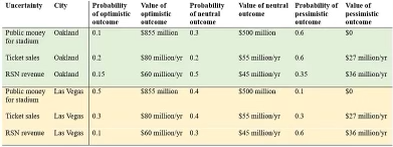
Существуют методы, которые выходят за рамки этого блога, чтобы запросить у лица, принимающего решения, предварительные убеждения о вероятных последствиях этих неопределенностей и вероятностях каждого из них. Кроме того, я сомневаюсь, что Джон Фишер готов комментировать мой блог. Итак, тем временем я буду использовать информацию, которую я собрал из этих веб-источников, чтобы представить несколько возможных сценариев для каждой неопределенности.
Каков наш временной горизонт принятия решения?
Конечно, доходы — это годовые цифры, и стадион должен прослужить гораздо дольше года. Временные горизонты могут различаться в зависимости от контекста решения и того, как лицо, принимающее решение, рассматривает вероятность изменения ландшафта. В терминах науки о данных это соответствует дрейфу данных, когда данные, используемые для обучения модели, отличаются от текущих данных. А пока давайте предположим, что эти оценки останутся довольно стабильными в течение десятилетия, и используем 10-летний временной горизонт с 3%-ной ставкой дисконтирования наших годовых затрат.
Как выглядит дерево решений?
Для лучшего понимания дерева решений предлагаем вам изучить статьи о том, как внедрять их с нуля и как их реализовать.
Теперь, когда мы определили все компоненты нашего дерева решений, пришло время построить дерево. Концептуально вот как это выглядит:
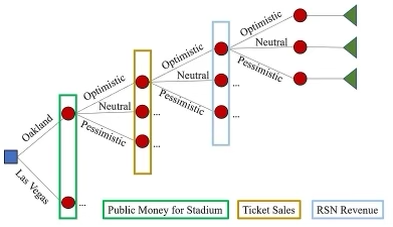
Квадратный узел — это узел принятия решения, круглые узлы — это случайные узлы, а треугольные узлы — конечные узлы. Из-за нехватки места все дерево не видно на изображении, но каждый узел также имеет связанную вероятность и значение.
Как построить модель на Python?
При анализе решений после построения нашего дерева решений мы можем определить наилучшее решение, «откатив» дерево. В этом примере мы предполагаем, что лицо, принимающее решение, принимает рациональное решение (также известное как ожидаемая ценность). Итак, мы начинаем с табулирования значения, связанного с терминальным состоянием, если оно применимо. Это станет нашим промежуточным итогом или ожидаемым значением. В данном случае это неприменимо, поэтому мы начинаем с суммы 0 долларов. Затем мы итеративно вычисляем ожидаемое значение каждого набора узлов слева от конечных узлов и добавляем его к промежуточному итогу или ожидаемому значению. В итоге мы получим одно ожидаемое значение решения остаться в Окленде и одно ожидаемое значение решения переехать в Лас-Вегас.
Давайте начнем с простой настройки нашего базового сценария. Мы собираемся использовать подход создания фрейма данных для всех возможных комбинаций сценариев решений, государственных денег, продажи билетов и доходов RSN.
import numpy as np
import pandas as pd
# Create data frame of all possible outcomes
decision_list = ['Oakland', 'Las Vegas']
# First Node
chance_node_stadium_money_scenarios = ['Optimistic', 'Neutral', 'Pessimistic']
chance_node_stadium_money_probabilities_oakland = [0.1, 0.3, 0.6]
chance_node_stadium_money_probabilities_vegas = [0.5, 0.4, 0.1]
chance_node_stadium_money_values = [855, 500, 0]
#Second Node
chance_node_ticket_sales_scenarios = ['Optimistic', 'Neutral', 'Pessimistic']
chance_node_ticket_sales_probabilities_oakland = [0.2, 0.2, 0.6]
chance_node_ticket_sales_probabilities_vegas = [0.3, 0.4, 0.3]
chance_node_ticket_sales_values_per_year = [80, 55, 27]
# Third Node
chance_node_rsn_revenue_scenarios = ['Optimistic', 'Neutral', 'Pessimistic']
chance_node_rsn_revenue_probabilities_oakland = [0.15, 0.5, 0.35]
chance_node_rsn_revenue_probabilities_vegas = [0.1, 0.3, 0.6]
chance_node_rsn_revenue_values_per_year = [60, 45, 36]
# Convert annual values to NPV of 10 year time horizon
time_horizon = 10 # years
discount_rate = 0.03 # per year
chance_node_ticket_sales_values = [val * (1 - (1/((1 + discount_rate)**time_horizon)))/discount_rate for val in chance_node_ticket_sales_values_per_year]
chance_node_rsn_revenue_values = [val * (1 - (1/((1 + discount_rate)**time_horizon)))/discount_rate for val in chance_node_rsn_revenue_values_per_year]
# Create data frame of all possible scenarios
decision_list_list_for_df = []
chance_node_stadium_money_list_for_df = []
chance_node_stadium_money_probability_list_for_df = []
chance_node_stadium_money_value_list_for_df = []
chance_node_ticket_sales_list_for_df = []
chance_node_ticket_sales_probability_list_for_df = []
chance_node_ticket_sales_value_list_for_df = []
chance_node_rsn_revenue_list_for_df = []
chance_node_rsn_revenue_probability_list_for_df = []
chance_node_rsn_revenue_value_list_for_df = []
for i in decision_list:
for j in range(len(chance_node_stadium_money_scenarios)):
for k in range(len(chance_node_rsn_revenue_scenarios)):
for m in range(len(chance_node_rsn_revenue_scenarios)):
decision_list_list_for_df.append(i)
chance_node_stadium_money_list_for_df.append(chance_node_stadium_money_scenarios[j])
chance_node_stadium_money_value_list_for_df.append(chance_node_stadium_money_values[j])
chance_node_ticket_sales_list_for_df.append(chance_node_ticket_sales_scenarios[k])
chance_node_ticket_sales_value_list_for_df.append(chance_node_ticket_sales_values[k])
chance_node_rsn_revenue_list_for_df.append(chance_node_rsn_revenue_scenarios[m])
chance_node_rsn_revenue_value_list_for_df.append(chance_node_rsn_revenue_values[m])
if i == 'Oakland':
chance_node_stadium_money_probability_list_for_df.append(chance_node_stadium_money_probabilities_oakland[j])
chance_node_ticket_sales_probability_list_for_df.append(chance_node_ticket_sales_probabilities_oakland[k])
chance_node_rsn_revenue_probability_list_for_df.append(chance_node_rsn_revenue_probabilities_oakland[m])
elif i == 'Las Vegas':
chance_node_stadium_money_probability_list_for_df.append(chance_node_stadium_money_probabilities_vegas[j])
chance_node_ticket_sales_probability_list_for_df.append(chance_node_ticket_sales_probabilities_vegas[k])
chance_node_rsn_revenue_probability_list_for_df.append(chance_node_rsn_revenue_probabilities_vegas[m])
decision_tree_df = pd.DataFrame(list(zip(decision_list_list_for_df, chance_node_stadium_money_list_for_df,
chance_node_stadium_money_probability_list_for_df,
chance_node_stadium_money_value_list_for_df,
chance_node_ticket_sales_list_for_df,
chance_node_ticket_sales_probability_list_for_df,
chance_node_ticket_sales_value_list_for_df,
chance_node_rsn_revenue_list_for_df,
chance_node_rsn_revenue_probability_list_for_df,
chance_node_rsn_revenue_value_list_for_df)),
columns = ['Decision',
'Stadium_Money_Result', 'Stadium_Money_Prob', 'Stadium_Money_Value',
'Ticket_Sales_Result', 'Ticket_Sales_Prob', 'Ticket_Sales_Value',
'RSN_Revenue_Result', 'RSN_Revenue_Prob', 'RSN_Revenue_Value'])Теперь, если вы напечатаете свое дерево решений, вы получите фрейм данных pandas из 54 строк и 10 столбцов. Мы можем легко откатить дерево решений, творчески используя функции группировки и слияния. Давайте начнем с подсчета ожидаемого значения доходов RSN для каждой комбинации решений, денег стадиона и продаж билетов:
decision_tree_df['RSN_EV'] = decision_tree_df['RSN_Revenue_Prob'] * decision_tree_df['RSN_Revenue_Value']
# Consolidate the RSN_EV values
RSN_rollback_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob', 'Ticket_Sales_Result', 'Ticket_Sales_Prob'])['RSN_EV'].sum().reset_index()
# Keep the rest of the columns
decision_tree_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob', 'Ticket_Sales_Result', 'Ticket_Sales_Prob'])['Stadium_Money_Value', 'Ticket_Sales_Value'].mean().reset_index()
# merge two dataframes
decision_tree_df = pd.merge(decision_tree_df, RSN_rollback_df, on = ['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob', 'Ticket_Sales_Result', 'Ticket_Sales_Prob'])Результирующая таблица уменьшилась, и теперь вы можете визуально увидеть ожидаемое значение отката узлов дохода RSN.
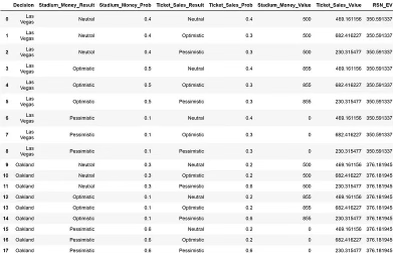
Повторение процесса с продажей билетов. У нас есть следующий код:
decision_tree_df['Ticket_Sales_RSN_EV'] = decision_tree_df['Ticket_Sales_Prob'] * decision_tree_df['Ticket_Sales_Value'] + decision_tree_df['RSN_EV']
# Consolidate the Ticket Sales and RSN_EV values
ticket_sales_rollback_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob'])['Ticket_Sales_RSN_EV'].sum().reset_index()
# Keep the rest of the columns
decision_tree_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob'])['Stadium_Money_Value'].mean().reset_index()
# merge two dataframes
decision_tree_df = pd.merge(decision_tree_df, ticket_sales_rollback_df, on = ['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob'])И вывод:
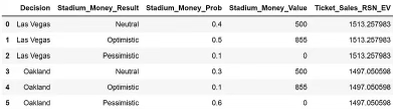
Наконец, повторяя для стадиона вклад государственных денег:
decision_tree_df['Stadium_Money_Ticket_Sales_RSN_EV'] = decision_tree_df['Stadium_Money_Prob'] * decision_tree_df['Stadium_Money_Value'] + decision_tree_df['Ticket_Sales_RSN_EV']
# Consolidate the Stadium Money, Ticket Sales, and RSN_EV values
decision_tree_df = decision_tree_df.groupby(['Decision'])['Stadium_Money_Ticket_Sales_RSN_EV'].sum().reset_index()
Здесь мы видим, что модель рассчитывает, что в течение 10 лет ожидаемая стоимость пребывания в Окленде составляет 4,7 миллиарда долларов, а ожидаемая стоимость переезда в Лас-Вегас - 5,2 миллиарда долларов.
Как мы можем обобщить модель?
Конечно, и в наших данных, и в нашей модели есть неопределенность, и есть много разных сценариев, которые мы могли бы протестировать. Естественно, мы можем попытаться определить некоторые пороговые значения или сценарии, при которых решение меняется с пребывания в Окленде на переезд в Лас-Вегас (или наоборот). Эти точки принятия решений могут служить полезным набором «бизнес-правил» для лиц, принимающих решения, и могут помочь нам, специалистам по данным, извлекать действенные рекомендации из нашего анализа.
Есть много способов достичь этой цели, но в этом блоге мы будем использовать метамоделирование машинного обучения. Мета-моделирование включает в себя разработку более быстрой (а иногда и более простой) модели исходной математической или имитационной модели, которая принимает те же входные данные и дает очень похожие выходные данные [7]. В этом случае мы будем использовать вероятностный анализ чувствительности для проверки большого пространства параметров дерева решений анализа решений и отметить результирующее решение для каждого набора параметров. Затем мы обучим модель классификации дерева решений машинного обучения, используя набор параметров в качестве признаков и полученное решение в качестве меток для нашей модели машинного обучения. Преимущество модели машинного обучения заключается в том, что она раскрывает для нас сложные взаимосвязи, которые было бы трудно расшифровать только с помощью многомерного анализа чувствительности. Мы надеемся, что мы сможем получить достаточно точности от неглубокого дерева, чтобы описать сценарии, в которых пятерки должны остаться в Окленде, а не переехать в Лас-Вегас.
Во-первых, мы начинаем с разработки вероятностного анализа чувствительности. Для этого примера мы предположим, что долларовые значения узлов шансов останутся прежними, но вероятности различных результатов будут различаться. Поскольку мы знаем, что вероятности будут варьироваться между значениями 0 и 1, мы предположим, что вероятности всех сценариев равновероятны, и смоделируем их, используя равномерное распределение с минимальным значением 0 и максимальным значением 1. После трехкратной выборки из равномерного распределения (один для каждого оптимистического, нейтрального и пессимистического сценария) мы нормализуем результаты таким образом, чтобы сумма трех вероятностей составляла 1.
# Number of simulations
n_sim = 5000
# Track scenarios
oakland_stadium_money_probabilities_optimistic_list = []
oakland_stadium_money_probabilities_neutral_list = []
oakland_stadium_money_probabilities_pessimistic_list = []
oakland_ticket_sales_probabilities_optimistic_list = []
oakland_ticket_sales_probabilities_neutral_list = []
oakland_ticket_sales_probabilities_pessimistic_list = []
oakland_rsn_revenue_probabilities_optimistic_list = []
oakland_rsn_revenue_probabilities_neutral_list = []
oakland_rsn_revenue_probabilities_pessimistic_list = []
vegas_stadium_money_probabilities_optimistic_list = []
vegas_stadium_money_probabilities_neutral_list = []
vegas_stadium_money_probabilities_pessimistic_list = []
vegas_ticket_sales_probabilities_optimistic_list = []
vegas_ticket_sales_probabilities_neutral_list = []
vegas_ticket_sales_probabilities_pessimistic_list = []
vegas_rsn_revenue_probabilities_optimistic_list = []
vegas_rsn_revenue_probabilities_neutral_list = []
vegas_rsn_revenue_probabilities_pessimistic_list = []
oakland_EV_list = []
vegas_EV_list = []
decision_list = []
# Create data frame of all possible outcomes
decision_list = ['Oakland', 'Las Vegas']
# First Node
chance_node_stadium_money_scenarios = ['Optimistic', 'Neutral', 'Pessimistic']
chance_node_stadium_money_values = [855, 500, 0]
#Second Node
chance_node_ticket_sales_scenarios = ['Optimistic', 'Neutral', 'Pessimistic']
chance_node_ticket_sales_values_per_year = [80, 55, 27]
# Third Node
chance_node_rsn_revenue_scenarios = ['Optimistic', 'Neutral', 'Pessimistic']
chance_node_rsn_revenue_values_per_year = [60, 45, 36]
# Convert annual values to NPV of 10 year time horizon
time_horizon = 10 # years
discount_rate = 0.03 # per year
chance_node_ticket_sales_values = [val * (1 - (1/((1 + discount_rate)**time_horizon)))/discount_rate for val in chance_node_ticket_sales_values_per_year]
chance_node_rsn_revenue_values = [val * (1 - (1/((1 + discount_rate)**time_horizon)))/discount_rate for val in chance_node_rsn_revenue_values_per_year]
# Run the probabilistic sensitivity analysis n_sim times
for n in range(n_sim):
## Set up tree
#First node
chance_node_stadium_money_probabilities_oakland = np.random.uniform(0,1,3)
chance_node_stadium_money_probabilities_oakland = chance_node_stadium_money_probabilities_oakland / np.sum(chance_node_stadium_money_probabilities_oakland)
chance_node_stadium_money_probabilities_vegas = np.random.uniform(0,1,3)
chance_node_stadium_money_probabilities_vegas = chance_node_stadium_money_probabilities_vegas / np.sum(chance_node_stadium_money_probabilities_vegas)
#Second Node
chance_node_ticket_sales_probabilities_oakland = np.random.uniform(0,1,3)
chance_node_ticket_sales_probabilities_oakland = chance_node_ticket_sales_probabilities_oakland / np.sum(chance_node_ticket_sales_probabilities_oakland)
chance_node_ticket_sales_probabilities_vegas = np.random.uniform(0,1,3)
chance_node_ticket_sales_probabilities_vegas = chance_node_ticket_sales_probabilities_vegas / np.sum(chance_node_ticket_sales_probabilities_vegas)
# Third Node
chance_node_rsn_revenue_probabilities_oakland = np.random.uniform(0,1,3)
chance_node_rsn_revenue_probabilities_oakland = chance_node_rsn_revenue_probabilities_oakland / np.sum(chance_node_rsn_revenue_probabilities_oakland)
chance_node_rsn_revenue_probabilities_vegas = np.random.uniform(0,1,3)
chance_node_rsn_revenue_probabilities_vegas = chance_node_rsn_revenue_probabilities_vegas / np.sum(chance_node_rsn_revenue_probabilities_vegas)
# Evaluate Tree
# Create data frame of all possible scenarios
decision_list_list_for_df = []
chance_node_stadium_money_list_for_df = []
chance_node_stadium_money_probability_list_for_df = []
chance_node_stadium_money_value_list_for_df = []
chance_node_ticket_sales_list_for_df = []
chance_node_ticket_sales_probability_list_for_df = []
chance_node_ticket_sales_value_list_for_df = []
chance_node_rsn_revenue_list_for_df = []
chance_node_rsn_revenue_probability_list_for_df = []
chance_node_rsn_revenue_value_list_for_df = []
for i in decision_list:
for j in range(len(chance_node_stadium_money_scenarios)):
for k in range(len(chance_node_rsn_revenue_scenarios)):
for m in range(len(chance_node_rsn_revenue_scenarios)):
decision_list_list_for_df.append(i)
chance_node_stadium_money_list_for_df.append(chance_node_stadium_money_scenarios[j])
chance_node_stadium_money_value_list_for_df.append(chance_node_stadium_money_values[j])
chance_node_ticket_sales_list_for_df.append(chance_node_ticket_sales_scenarios[k])
chance_node_ticket_sales_value_list_for_df.append(chance_node_ticket_sales_values[k])
chance_node_rsn_revenue_list_for_df.append(chance_node_rsn_revenue_scenarios[m])
chance_node_rsn_revenue_value_list_for_df.append(chance_node_rsn_revenue_values[m])
if i == 'Oakland':
chance_node_stadium_money_probability_list_for_df.append(chance_node_stadium_money_probabilities_oakland[j])
chance_node_ticket_sales_probability_list_for_df.append(chance_node_ticket_sales_probabilities_oakland[k])
chance_node_rsn_revenue_probability_list_for_df.append(chance_node_rsn_revenue_probabilities_oakland[m])
elif i == 'Las Vegas':
chance_node_stadium_money_probability_list_for_df.append(chance_node_stadium_money_probabilities_vegas[j])
chance_node_ticket_sales_probability_list_for_df.append(chance_node_ticket_sales_probabilities_vegas[k])
chance_node_rsn_revenue_probability_list_for_df.append(chance_node_rsn_revenue_probabilities_vegas[m])
decision_tree_df = pd.DataFrame(list(zip(decision_list_list_for_df, chance_node_stadium_money_list_for_df,
chance_node_stadium_money_probability_list_for_df,
chance_node_stadium_money_value_list_for_df,
chance_node_ticket_sales_list_for_df,
chance_node_ticket_sales_probability_list_for_df,
chance_node_ticket_sales_value_list_for_df,
chance_node_rsn_revenue_list_for_df,
chance_node_rsn_revenue_probability_list_for_df,
chance_node_rsn_revenue_value_list_for_df)),
columns = ['Decision',
'Stadium_Money_Result', 'Stadium_Money_Prob', 'Stadium_Money_Value',
'Ticket_Sales_Result', 'Ticket_Sales_Prob', 'Ticket_Sales_Value',
'RSN_Revenue_Result', 'RSN_Revenue_Prob', 'RSN_Revenue_Value'])
decision_tree_df['RSN_EV'] = decision_tree_df['RSN_Revenue_Prob'] * decision_tree_df['RSN_Revenue_Value']
# Consolidate the RSN_EV values
RSN_rollback_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob', 'Ticket_Sales_Result', 'Ticket_Sales_Prob'])['RSN_EV'].sum().reset_index()
# Keep the rest of the columns
decision_tree_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob', 'Ticket_Sales_Result', 'Ticket_Sales_Prob'])['Stadium_Money_Value', 'Ticket_Sales_Value'].mean().reset_index()
# merge two dataframes
decision_tree_df = pd.merge(decision_tree_df, RSN_rollback_df, on = ['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob', 'Ticket_Sales_Result', 'Ticket_Sales_Prob'])
decision_tree_df['Ticket_Sales_RSN_EV'] = decision_tree_df['Ticket_Sales_Prob'] * decision_tree_df['Ticket_Sales_Value'] + decision_tree_df['RSN_EV']
# Consolidate the Ticket Sales and RSN_EV values
ticket_sales_rollback_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob'])['Ticket_Sales_RSN_EV'].sum().reset_index()
# Keep the rest of the columns
decision_tree_df = decision_tree_df.groupby(['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob'])['Stadium_Money_Value'].mean().reset_index()
# merge two dataframes
decision_tree_df = pd.merge(decision_tree_df, ticket_sales_rollback_df, on = ['Decision', 'Stadium_Money_Result', 'Stadium_Money_Prob'])
decision_tree_df['Stadium_Money_Ticket_Sales_RSN_EV'] = decision_tree_df['Stadium_Money_Prob'] * decision_tree_df['Stadium_Money_Value'] + decision_tree_df['Ticket_Sales_RSN_EV']
# Consolidate the Stadium Money, Ticket Sales, and RSN_EV values
decision_tree_df = decision_tree_df.groupby(['Decision'])['Stadium_Money_Ticket_Sales_RSN_EV'].sum().reset_index()
# Fill out lists for meta-model inputs
oakland_stadium_money_probabilities_optimistic_list.append(chance_node_stadium_money_probabilities_oakland[0])
oakland_stadium_money_probabilities_neutral_list.append(chance_node_stadium_money_probabilities_oakland[1])
oakland_stadium_money_probabilities_pessimistic_list.append(chance_node_stadium_money_probabilities_oakland[2])
oakland_ticket_sales_probabilities_optimistic_list.append(chance_node_ticket_sales_probabilities_oakland[0])
oakland_ticket_sales_probabilities_neutral_list.append(chance_node_ticket_sales_probabilities_oakland[1])
oakland_ticket_sales_probabilities_pessimistic_list.append(chance_node_ticket_sales_probabilities_oakland[2])
oakland_rsn_revenue_probabilities_optimistic_list.append(chance_node_rsn_revenue_probabilities_oakland[0])
oakland_rsn_revenue_probabilities_neutral_list.append(chance_node_rsn_revenue_probabilities_oakland[1])
oakland_rsn_revenue_probabilities_pessimistic_list.append(chance_node_rsn_revenue_probabilities_oakland[2])
vegas_stadium_money_probabilities_optimistic_list.append(chance_node_stadium_money_probabilities_vegas[0])
vegas_stadium_money_probabilities_neutral_list.append(chance_node_stadium_money_probabilities_vegas[1])
vegas_stadium_money_probabilities_pessimistic_list.append(chance_node_stadium_money_probabilities_vegas[2])
vegas_ticket_sales_probabilities_optimistic_list.append(chance_node_ticket_sales_probabilities_vegas[0])
vegas_ticket_sales_probabilities_neutral_list.append(chance_node_ticket_sales_probabilities_vegas[1])
vegas_ticket_sales_probabilities_pessimistic_list.append(chance_node_ticket_sales_probabilities_vegas[2])
vegas_rsn_revenue_probabilities_optimistic_list.append(chance_node_rsn_revenue_probabilities_vegas[0])
vegas_rsn_revenue_probabilities_neutral_list.append(chance_node_rsn_revenue_probabilities_vegas[1])
vegas_rsn_revenue_probabilities_pessimistic_list.append(chance_node_rsn_revenue_probabilities_vegas[2])
oakland_EV_list.append(decision_tree_df['Stadium_Money_Ticket_Sales_RSN_EV'][0])
vegas_EV_list.append(decision_tree_df['Stadium_Money_Ticket_Sales_RSN_EV'][1])
print(n)Теперь мы можем поместить результаты в новый фрейм данных, который мы можем использовать для обучения нашей модели машинного обучения:
decision_tree_psa_data_df = pd.DataFrame(list(zip(oakland_stadium_money_probabilities_optimistic_list,
oakland_stadium_money_probabilities_neutral_list,
oakland_stadium_money_probabilities_pessimistic_list,
oakland_ticket_sales_probabilities_optimistic_list,
oakland_ticket_sales_probabilities_neutral_list,
oakland_ticket_sales_probabilities_pessimistic_list,
oakland_rsn_revenue_probabilities_optimistic_list,
oakland_rsn_revenue_probabilities_neutral_list,
oakland_rsn_revenue_probabilities_pessimistic_list,
vegas_stadium_money_probabilities_optimistic_list,
vegas_stadium_money_probabilities_neutral_list,
vegas_stadium_money_probabilities_pessimistic_list,
vegas_ticket_sales_probabilities_optimistic_list,
vegas_ticket_sales_probabilities_neutral_list,
vegas_ticket_sales_probabilities_pessimistic_list,
vegas_rsn_revenue_probabilities_optimistic_list,
vegas_rsn_revenue_probabilities_neutral_list,
vegas_rsn_revenue_probabilities_pessimistic_list,
oakland_EV_list, vegas_EV_list)),
columns = ['oakland_stad_mon_prob_optimistic',
'oakland_stad_mon_prob_neutral',
'oakland_stad_mon_prob_pessimistic',
'oakland_ticket_sales_prob_optimistic',
'oakland_ticket_sales_prob_neutral',
'oakland_ticket_sales_prob_pessimistic',
'oakland_rsn_rev_prob_optimistic',
'oakland_rsn_rev_prob_neutral',
'oakland_rsn_rev_prob_pessimistic',
'vegas_stad_mon_prob_optimistic',
'vegas_stad_mon_prob_neutral',
'vegas_stad_mon_prob_pessimistic',
'vegas_ticket_sales_prob_optimistic',
'vegas_ticket_sales_prob_neutral',
'vegas_ticket_sales_prob_pessimistic',
'vegas_rsn_rev_prob_optimistic',
'vegas_rsn_rev_prob_neutral',
'vegas_rsn_rev_prob_pessimistic',
'oakland_EV', 'vegas_EV'])
# Add decision based on EV
decision_tree_psa_data_df['decision'] = 'Oakland'
decision_tree_psa_data_df.loc[decision_tree_psa_data_df['vegas_EV'] > decision_tree_psa_data_df['oakland_EV'],'decision'] = 'Las Vegas'Теперь мы обучим базовое дерево решений машинного обучения, используя учебный пакет sci-kit. Поскольку входные данные представляют собой вероятности от 0 до 1, и мы используем древовидную модель, нам не нужно будет выполнять масштабирование или разработку каких-либо функций. В целях визуализации для блога я ограничил глубину дерева до 3. Однако чем больше глубина дерева, тем выше вероятность достижения большей точности.
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn import tree
#Features
X = decision_tree_psa_data_df.drop(['oakland_EV', 'vegas_EV', 'decision'], axis = 1)
#labels
y = decision_tree_psa_data_df['decision']
# split into train (70%) and test set (30%)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=32)
# Create decision tree model with maximum depth of 3 to keep recommendation managable
dec_tree_model = tree.DecisionTreeClassifier(random_state=32, max_depth = 3, class_weight = 'balanced')
dec_tree_model = dec_tree_model.fit(X_train, y_train)Наша модель получила приличную, но не идеальную AUC почти 0,8. (AUC — это способ измерения точности модели на основе показателей истинных и ложноположительных результатов. Чтобы узнать больше о показателях точности модели, ознакомьтесь с моим предыдущим блогом об оценке точности предсказанных результатов ESPN в фэнтези-футболе здесь.) Это достаточно респектабельно, чтобы мы могли продолжить упражнение. Конечно, существует несколько способов сделать классификатор дерева решений более точным, включая увеличение максимальной глубины, настройку гиперпараметров или запуск большего количества симуляций для увеличения количества данных.
from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, dec_tree_model.predict_proba(X_test)[:, 1])Теперь, когда мы удовлетворены производительностью, мы можем визуально изучить дерево решений поезда. Каждое разделение в дереве представляет другое измерение набора бизнес-правил. В каждом блоке (или листе) напечатанного дерева первая строка будет представлять правило, используемое моделью для разделения данных, вторая строка — это индекс Джини, который описывает распределение классов в листе (где 0,5 представляет собой равное количество каждого класса, а 0 или 1 представляет только один класс), третья строка показывает количество образцов каждого класса, а четвертая строка показывает метку, которую модель присваивает всем образцам в этом листе. Мы можем распечатать полученное дерево ниже:
# Plot decision tree results to see how decisions were made
import matplotlib.pyplot as plt
fig = plt.figure(figsize = (14,14))
tree.plot_tree(dec_tree_model, filled = True, feature_names = X.columns, fontsize = 8, class_names = ['Las Vegas', 'Oakland'])
plt.show()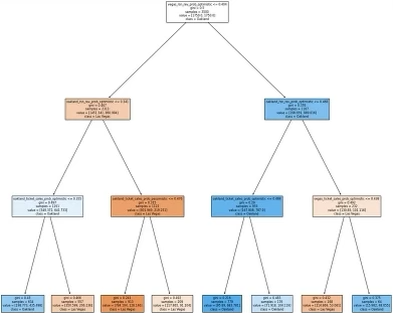
Из нашего дерева решений, основанного на машинном обучении, мы видим, что классификация того, должны ли пятерки остаться в Окленде или переехать в Лас-Вегас, основывалась сначала на вероятности оптимистического дохода RSN, а затем на вероятностях, связанных с продажей билетов в Окленде.
Лас-Вегас, вероятно, предпочтительнее, если:
- Вероятность оптимистичной выручки RSN в Лас-Вегасе больше 0,4 (за исключением случаев, когда вероятность оптимистичной выручки RSN в Окленде больше 0,341 И вероятность оптимистичной продажи билетов в Окленде больше 0,355)
- ИЛИ вероятность оптимистичной выручки RSN в Окленде меньше или равна 0,468 И вероятность оптимистичной продажи билетов в Лас-Вегасе больше 0,438.
Интересно, что, несмотря на всю болтовню в СМИ о государственном или частном финансировании нового стадиона, наша модель указывает на доходы RSN и продажи билетов. Разница может быть связана с нашим 10-летним горизонтом или может быть связана с тем, что организация ищет одобренный MLB повод покинуть Окленд. В любом случае, этот подход выдвигает на первый план важную информацию, которую команда специалистов по данным может донести до лиц, принимающих решения, для информирования бизнес-стратегии. Подобные методы могут превратить вашу модель из интересного теоретического упражнения в изменение взглядов топ-менеджеров.
Как мы проверяем модель машинного обучения?
Учитывая, что мы пытаемся сообщить об очень важном решении, важно убедиться, что наша модель устойчива к различиям во входных данных или несбалансированному набору меток классов. Как вы заметите, для учета последнего мы включили class_weight = ‘balanced’ при создании нашей модели машинного обучения. Чтобы учесть первое и для проверки модели, мы можем использовать оценку перекрестной проверки, чтобы увидеть, какими будут другие показатели производительности разделения обучения/тестирования:
# 10-fold cross-validation scores
cross_val_score(dec_tree_model, X, y, cv=10)Вывод следующий: массив ([0,724, 0,722, 0,718, 0,72, 0,722, 0,708, 0,732, 0,726, 0,76, 0,702]), который говорит нам, что в 10 различных возможных разделениях обучения/тестирования наша модель имела одинаковую производительность.
Что мы узнали?
Таким образом, мы перешли от бизнес-вопроса о перемещении бейсбольной команды «А» к откатыванию модели дерева решений для анализа решений, чтобы выяснить, почему «А» могут отправиться в Лас-Вегас, к использованию дерева решений с машинным обучением для обобщения наших результатов в легко усваиваемые бизнес-правила, которые руководство может использовать, чтобы решить, следует ли перемещать компанию или нет. Надеюсь, вы сможете использовать подобную методологию или подход для информирования лиц, принимающих решения, в вашей организации или в повседневной жизни.
Рекомендации
[1] Сутелан, Э., График переезда легкой атлетики в Лас-Вегас: спотыкания на стадионе, сбои в финансировании на пути к отъезду А из Окленда (2023 г.), The Sporting News
[2] Кентон, В., Анализ решений (DA): определение, использование и примеры (2022), Investopedia.
[3] Ховард Р. и Аббас А. Основы анализа решений (2014 г.)
[4] Морсс, Э., Финансы Высшей лиги бейсбола: что нам говорят цифры (2019), Morss Global Finance
[5] Грир Дж., Почему Рейдеры переехали в Лас-Вегас? Объяснение перехода франшизы в 2020 году из Окленда в Город грехов (2020), The Sporting News
[6] Андре, Д. Отчет: Рейдеры первыми по доходам от билетов НФЛ в 2021 году (2022), Fox 5 Las Vegas
[7] Маллой, Г. и Брандо, М. Когда массовая профилактика экономически эффективна для борьбы с эпидемиями? Сравнение подходов к принятию решений (2022 г.), Принятие медицинских решений
Весь код и данные можно найти на GitHub здесь: gspmalloy/oakland_as_decision_trees: Code for my blog “Decision analysis and trees in Python — The case of the Oakland A’s” (github.com)
Считаете ли вы, что пятёрки должны остаться в Окленде? Переехать в Вегас? Может, попробовать другой город? Каков ваш опыт использования машинного обучения для метамоделирования.