Кластеризация траектории GPS с помощью Python
Быстрый рост мобильных устройств привел к появлению огромного количества траекторий GPS, собранных службами на основе определения местоположения, геосоциальными сетями, транспортом или приложениями для совместного использования.
Кластеризация траекторий GPS все чаще используется во многих приложениях. Например, это может помочь определить частые маршруты или поездки. Сходство траектории можно использовать, чтобы определить, следует ли траектория определенному маршруту. Затем его можно использовать для отслеживания транспортных услуг, например, городских автобусов.
В этой статье я приведу краткое введение в быструю кластеризацию траекторий GPS. В этом решении используются библиотеки Python с открытым исходным кодом. Как правило, при кластеризации траекторий может возникнуть несколько проблем.
- Траектории GPS часто содержат много точек данных. Кластеризация может занять много времени.
- Соответствующие меры сходства необходимы для сравнения различных траекторий.
- Кластерный подход и настройка
- Визуализация траекторий и их скоплений
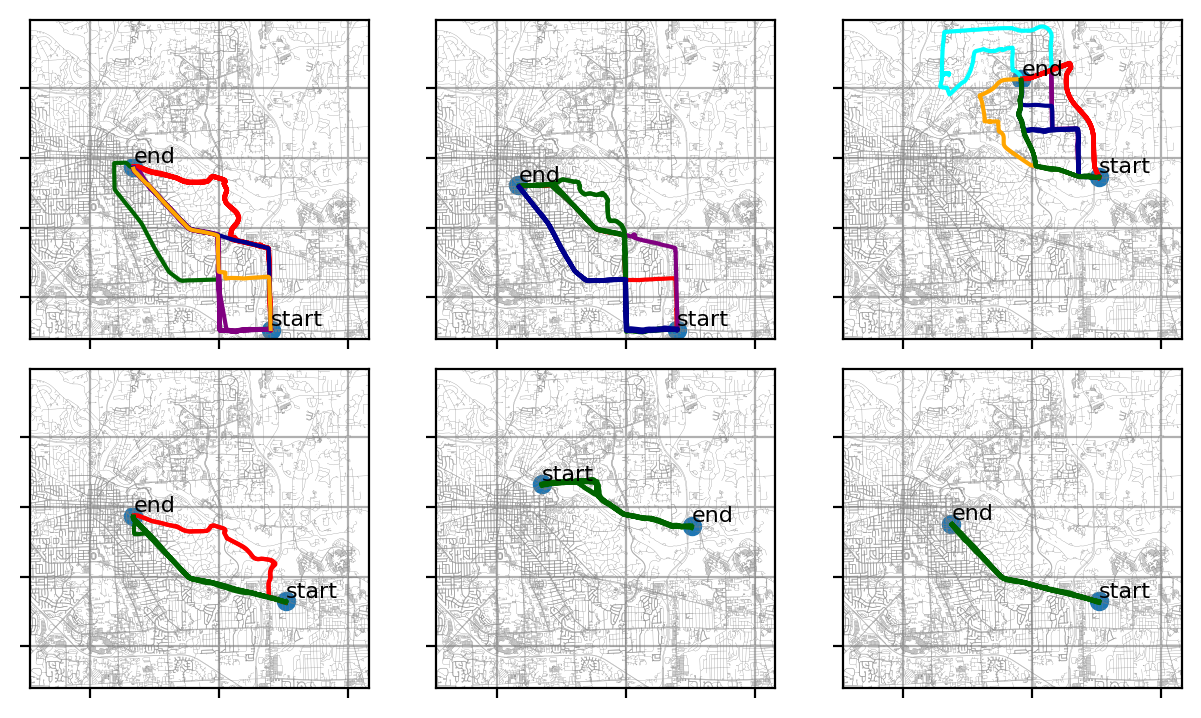
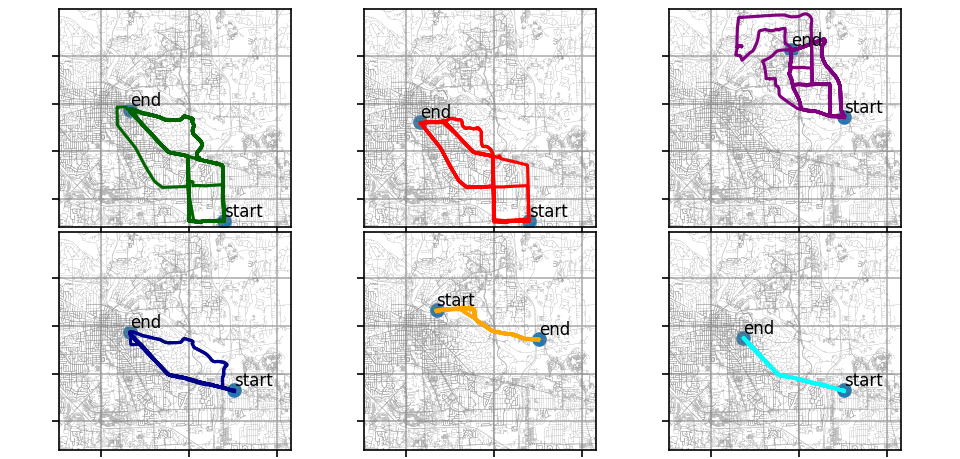
На эту тему есть ряд интересных статей. Однако решены не все вышеперечисленные проблемы. В этой статье я проиллюстрирую решение Python, охватывающее все эти области. Используемые здесь данные взяты из набора данных по энергии транспортного средства. Сначала к исходным данным был применен процесс кластеризации всех точек GPS. Затем я выбрал траектории для нескольких начально-конечных групп. Для простоты данные, представленные в этой статье, относятся к этим группам траекторий, как показано ниже:
Уменьшение точек данных траектории
Алгоритм Рамера-Дугласа-Пекера (RDP) - один из самых популярных методов уменьшения количества точек в ломаной линии. Цель этого алгоритма - найти подмножество точек для представления всей ломаной линии.
def rdp_with_index(points, indices, epsilon):
"""rdp with returned point indices
"""
dmax, index = 0.0, 0
for i in range(1, len(points) - 1):
d = point_line_distance(points[i], points[0], points[-1])
if d > dmax:
dmax, index = d, i
if dmax >= epsilon:
first_points, first_indices = rdp_with_index(points[:index+1], indices[:index+1], epsilon)
second_points, second_indices = rdp_with_index(points[index:], indices[index:], epsilon)
results = first_points[:-1] + second_points
results_indices = first_indices[:-1] + second_indices
else:
results, results_indices = [points[0], points[-1]], [indices[0], indices[-1]]
return results, results_indices
Параметр epsilon здесь установлен равным 10 (метрам). После RDP количество точек данных на траекториях значительно уменьшается по сравнению с исходными точками данных.
traj # data points original after RDP
0 266 21
1 276 36
2 239 34
...
Это способствует резкому сокращению времени вычисления матрицы расстояний.
distance matrix without RDP: 61.0960 seconds
distance matrix with RDP: 0.4899 seconds
Меры сходства траекторий и матрица расстояний
Существуют различные методы измерения сходства двух траекторий, например, расстояние Фреше, метод площади, как показано на следующем рисунке. Они могут быть рассчитаны с использованием пакета similaritymeasures.
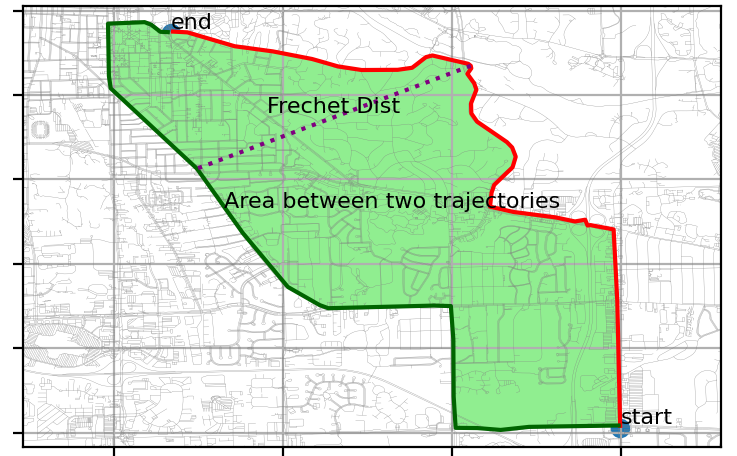
В примерах в этой статье расстояние Фреше используется для вычисления матрицы расстояний, как показано ниже. Также поддерживается мера сходства по площади.
def compute_distance_matrix(trajectories, method="Frechet"):
"""
:param method: "Frechet" or "Area"
"""
n = len(trajectories)
dist_m = np.zeros((n, n))
for i in range(n - 1):
p = trajectories[i]
for j in range(i + 1, n):
q = trajectories[j]
if method == "Frechet":
dist_m[i, j] = similaritymeasures.frechet_dist(p, q)
else:
dist_m[i, j] = similaritymeasures.area_between_two_curves(p, q)
dist_m[j, i] = dist_m[i, j]
return dist_m
DBSCAN кластеризация
Scikit-learn предоставляет несколько методов кластеризации. В этой статье я представляю DBSCAN с предварительно вычисленной матрицей. Параметры устанавливаются следующим образом:
- eps: 1000 (м) для расстояния Фреше, 300000 (м²) для измерения площади.
- min_samples: 1, чтобы убедиться, что все траектории будут сгруппированы в кластер.
Код приведен ниже.
def clustering_by_dbscan(distance_matrix, eps=1000):
"""
:param eps: unit m for Frechet distance, m^2 for Area
"""
cl = DBSCAN(eps=eps, min_samples=1, metric='precomputed')
cl.fit(distance_matrix)
return cl.labels_
Результаты и визуализация траектории
Matplotlib - это комплексная библиотека для визуализации на Python. Он предоставляет гибкие решения как для статической, так и для анимированной визуализации.
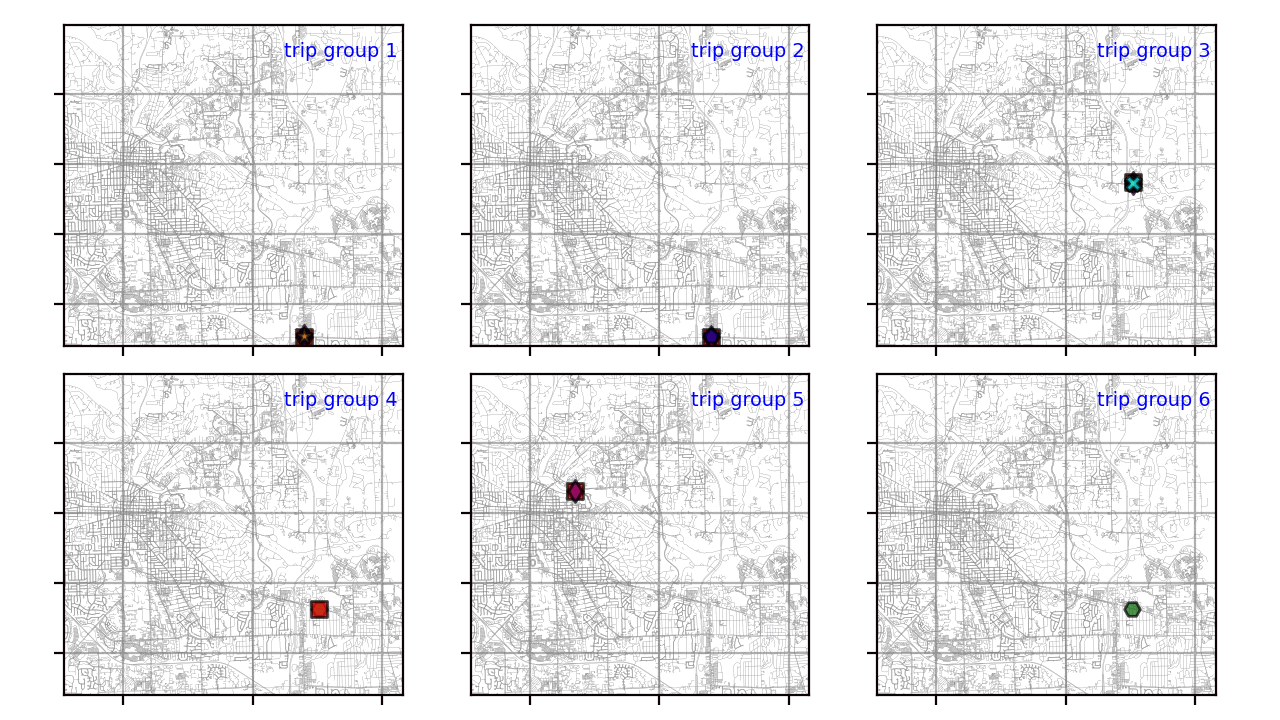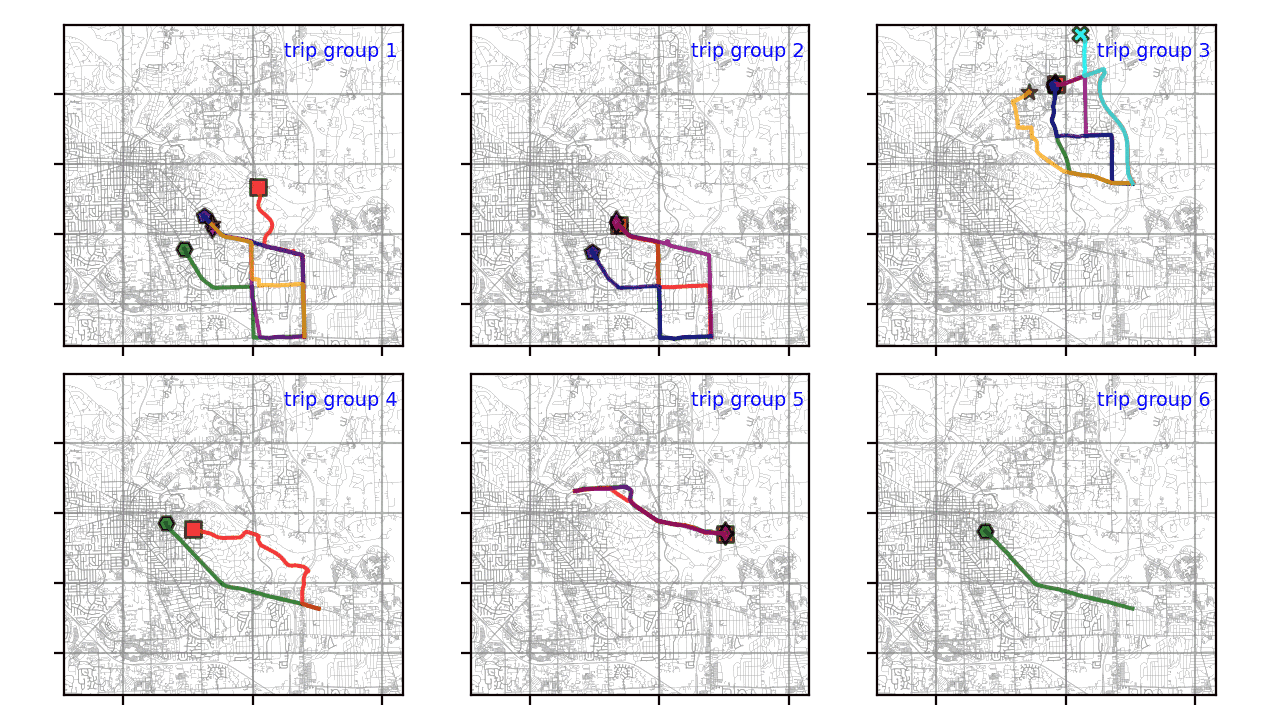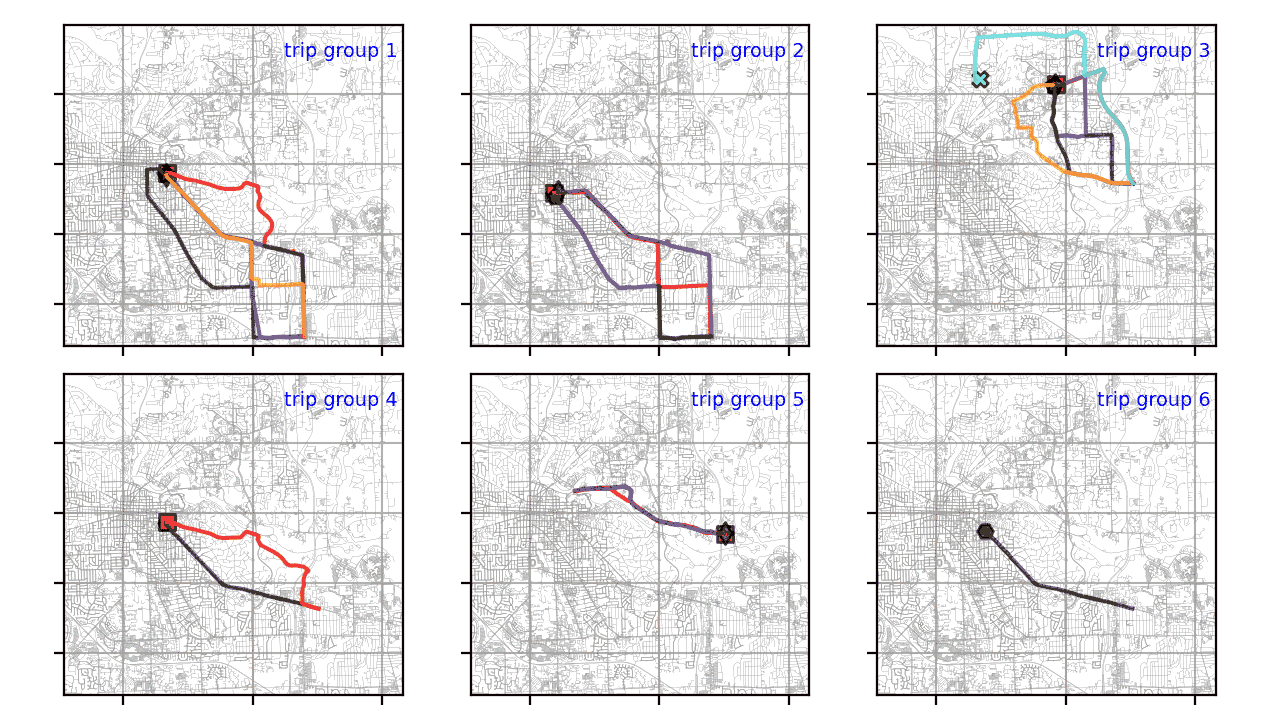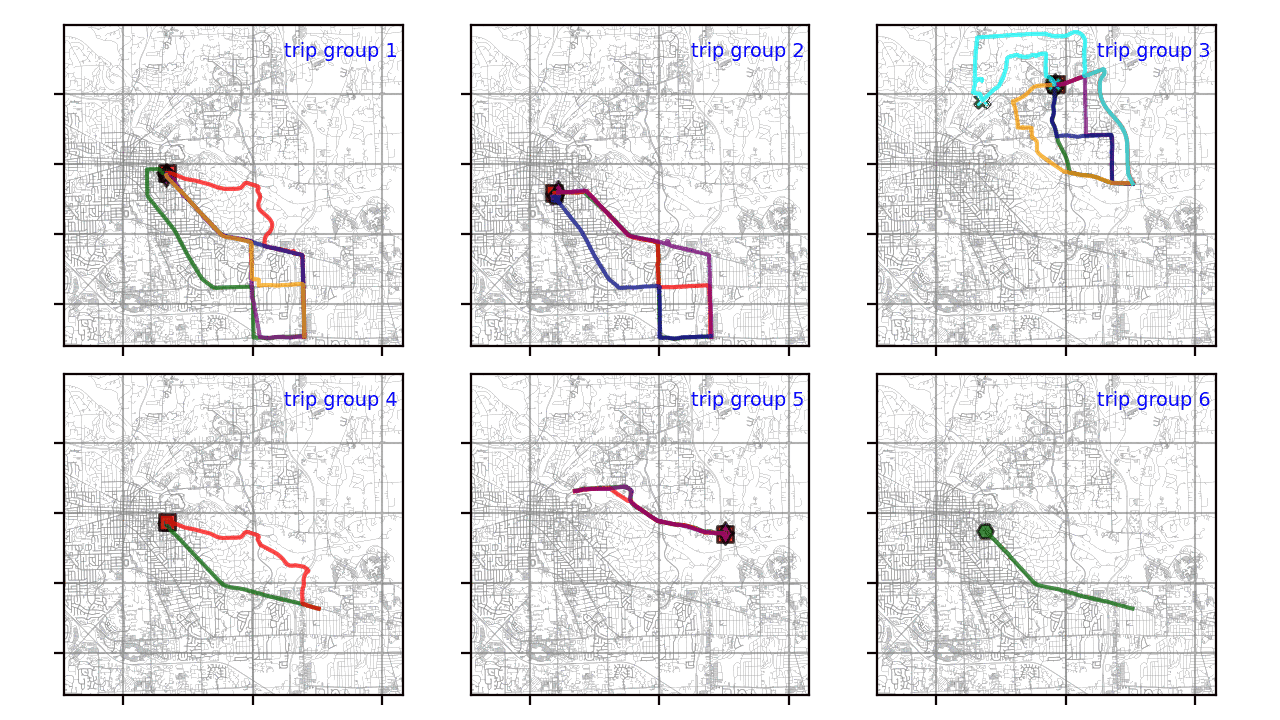
Результаты кластеризации для шести групп визуализируются с помощью подзаголовков в Matplotlib. Как показано ниже, большинство групп траекторий состоит из нескольких кластеров. Только две последние группы имеют один кластер по той причине, что сходство этих траекторий велико (расстояния Фреше меньше eps, т.е. 1000).