Линейная алгебра: Системы линейных уравнений и матриц с использованием Python

Линейная алгебра имеет решающее значение во многих областях науки и техники в целом. Она занимает центральное место почти во всех областях математики. Например, уравнения обычно используются для моделирования реальных проблем, а проблемы с несколькими переменными могут быть смоделированы с помощью систем уравнений. И даже системы нелинейных уравнений могут быть преобразованы в системы линейных уравнений. Таким образом, знание того, как решать эти системы линейных уравнений, может быть очень полезным в любой области современной науки. И как специалисту по обработке данных также важно хорошо разбираться в линейной алгебре, чтобы работать с большинством методов машинного обучения, особенно с алгоритмами глубокого обучения.
Линейное уравнение
Линейное уравнение — это уравнение, в котором старшая степень переменной всегда равна 1.
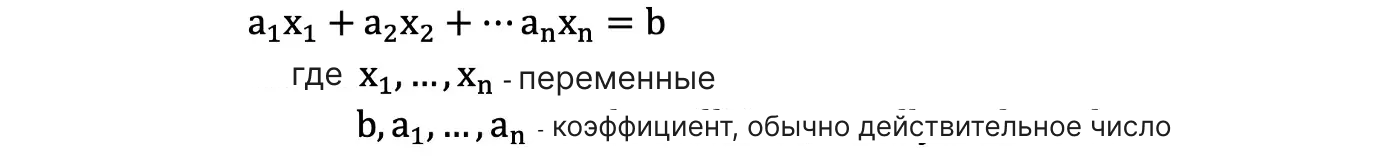
Линейная система
Система линейных уравнений - это серия линейных уравнений.
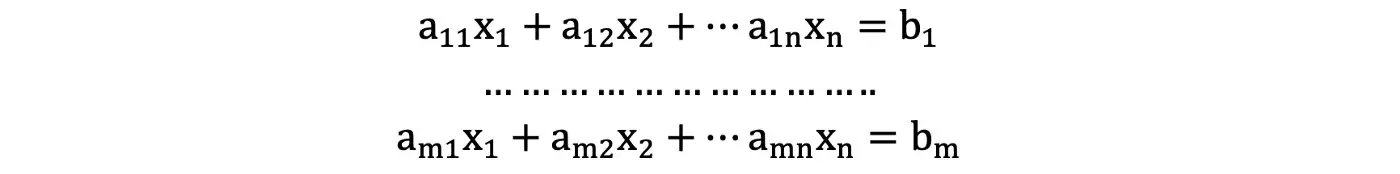
Приведенную выше систему линейных уравнений можно было бы переписать в виде матрицы, называемой дополненной матрицей. Матрица m x n представляет собой массив чисел с m строками и n столбцами, где m > 1 и n > 1. Каждое число в матрице называется записью.
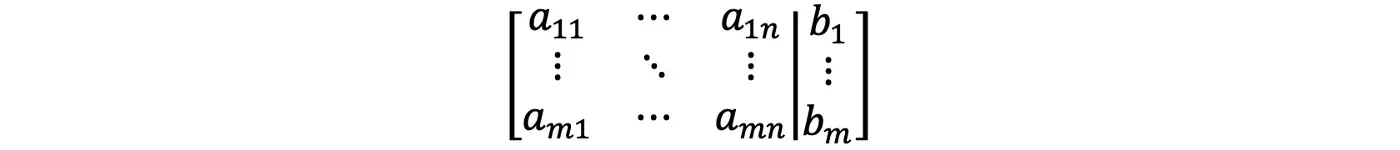
Однородные линейные системы
Линейная система называется однородной, если все постоянные члены bᵢ равны нулю.
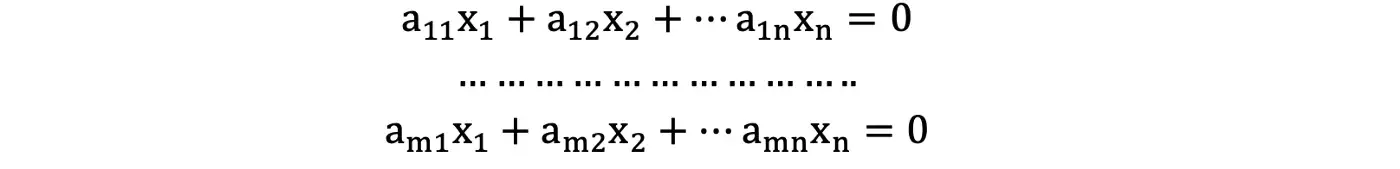
xᵢ = 0 называется тривиальным решением однородной системы.
Однородная система с большим количеством неизвестных, чем уравнений (n > m), имеет бесконечно много решений.
Возможные решения линейной системы
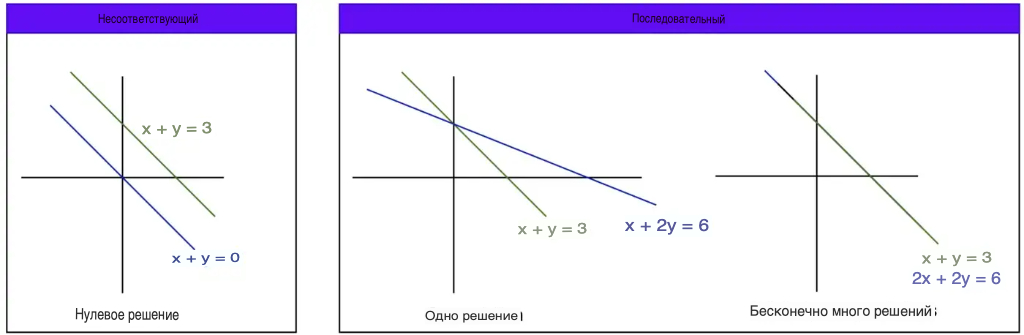
Возможны 3 случая решения линейных систем:
- Нулевое решение
- Одно решение
- Бесконечно много решений
Линейная система, не имеющая решения, называется несовместной. Если существует хотя бы одно решение, оно называется непротиворечивым.
Шаги для решения системы линейных уравнений с использованием элементарных операций со строками
Сокращение строк
Сокращение строк - это алгоритм для решения систем линейных уравнений. Уменьшение строк в матрице выполняется с помощью последовательности элементарных операций над строками для изменения матрицы до тех пор, пока нижний левый угол матрицы не будет заполнен нулями. Существует 3 типа операций со строками:
- Перестановка — уравнение заменяется другим, меняются местами 2 строки.
- Масштабирование — в уравнении обе части умножаются на ненулевую константу, умножается строка на ненулевую константу.
- Сводка — уравнение заменяется суммой самого себя и кратного другого уравнения, добавляя кратное одной строки к другой строке.
Форма эшелона строк
Система находится в форме эшелона строк, если
- Он выполнен в виде лестницы
- Ведущая запись (первая запись с ненулевым коэффициентом) в строке находится справа от ведущей записи в строке над ней
- Все ведущие записи 1

Процесс, который создает матрицу в эшелонированной форме, называется устранением Гаусса.
Уменьшенная форма эшелона
Система находится в форме уменьшенного эшелона, если
- Начальная запись в каждой ненулевой строке равна 1.
- Все остальные записи столбца, в котором встречается начальная запись 1, являются нулями.

Процесс, который создает матрицу в форме уменьшенного эшелона, называется устранением Гаусса-Жордана.
В эшелонированной форме первая переменная с ненулевым коэффициентом - это сводные переменные/ведущие переменные. Не ведущие переменные являются свободными переменными.
Примеры
Решите приведенную ниже систему уравнений:
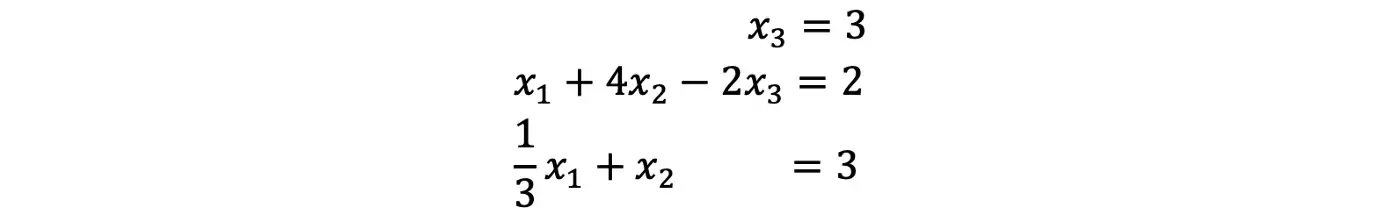
Сначала преобразуйте систему линейных уравнений в расширенную матрицу, а затем выполните серию элементарных операций над строками, чтобы решить ее в виде эшелона строк.

import sympy
import numpy as np
augmented_matrix = np.array([[0, 0, 1, 3], [1, 4, -2, 2], [1/3, 1, 0, 3]])
reduced_echlon_form = sympy.Matrix(augmented_matrix).rref()
reduced_echlon_form
import numpy as np
# coefficient matrix
coefficient_matrix = np.array([[0, 0, 1], [1, 4, -2], [1/3, 1, 0]])
# dependent variable values
dependent_variable_values = np.array([3, 2, 3])
# solving linear equation system
solution = np.linalg.solve(coefficient_matrix, dependent_variable_values)
solution
Вывод
В этом посте вы узнали об основах линейной алгебры, системах линейных уравнений и матрицах. Вы узнали, что представляют собой линейные уравнения и линейные системы, и 3 возможных решения линейной системы. Кроме того, вы узнали, как решать линейные уравнения, применяя последовательности операций над строками, чтобы преобразовать матрицы либо в эшелонированную, либо в редуцированную эшелонированную форму. Кроме того, вы также узнаете, какие пакеты программирования можно использовать для решения систем линейных уравнений.