Линейный и бинарный поиск с помощью JavaScript

JavaScript поставляется с некоторыми довольно удобными инструментами для поиска в массиве. Но с большим набором данных в O(N), такие методы как indexOf или find могут работать не так быстро как хотелось бы. Вместо этого мы можем использовать бинарный поиск для обхода массива и поиска только того что нам действительно нужно, игнорируя то, что нам явно не нужно, при этом давая нам сложность O(logn).
Предпосылки
Я буду использовать Big O Notation при сравнении производительности и сложности, с которыми вы можете ознакомиться здесь.
Входные данные
Вот некоторые отсортированные и несортированные наборы данных, оба из 50 элементов, на которые я буду ссылаться.
const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];
const sortedArr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50];
Линейный поиск
Это стандартное решение для перебора, я уверен, вы уже делали это тысячу раз. Мы просто говорим: «Мне нужно что-то, так что просматривайте все один за другим, пока не найдете это». Если элементов в миллион раз больше, это займет в миллион раз больше времени, и это может привести к долгому выполнению или даже зависанию браузера.
const linear = (arr, target) => {
let steps = 0;
for (let i = 0; i < arr.length; i++) {
steps++;
if (arr[i] === target) return `Found: ${arr[i]} in ${steps} steps`;
};
};
console.log(linear(unsortedArr, 40)); // 40 steps in 40 Milliseconds
console.log(linear(sortedArr, 40)); // 40 steps in 40 Milliseconds
Бинарный поиск
Грубое движение к результату, очевидно, является очень медленным и не масштабируемым решением. Вместо того, чтобы тратить ресурсы на поиск данных, которые, очевидно, не то, что нам нужно, мы можем использовать подход «разделяй и властвуй», чтобы каждая операция была сосредоточена на игнорировании того, что нам не нужно, вместо того, чтобы мучительно искать то, что мы хотим.
У нас есть три основных компонента, два указателя и одна ось. Каждый указатель начинается с любого конца массива с осью в центре. Затем мы проверяем, является ли то, что мы хотим, выше или ниже нашего центра, если выше, чем левый указатель перемещается в положение центра, в то время как центр перемещается в новую середину. Мы продолжаем работать до тех пор, пока наша точка не станет равна нашей цели.
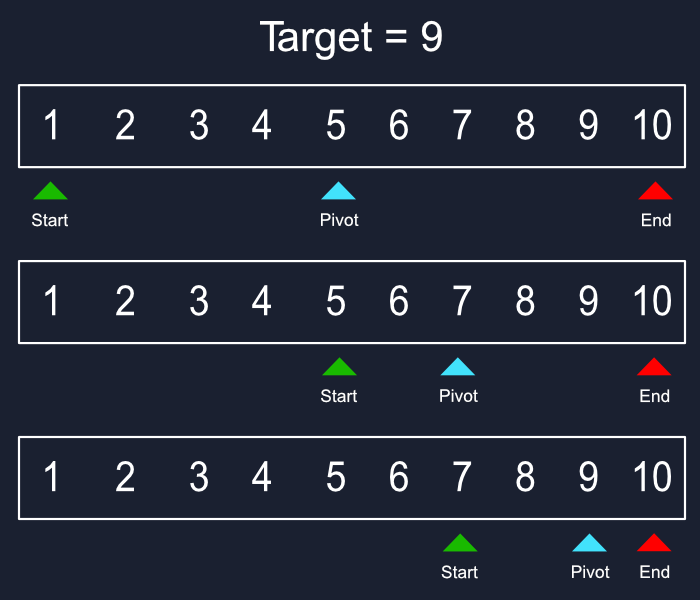
С каждым шагом мы разрезаем наш набор данных пополам, полностью игнорируя то, что нам не нужно, давая нам временную сложность O(log n). Если мы выполнили поиск числа в массиве из миллиона элементов, который занял десять шагов, поиск миллиарда элементов может занять всего 15-20 шагов.
const binary = (arr, target) => {
let start = 0;
let end = arr.length;
let pivot = Math.floor((start + end) / 2);
let steps = 0;
for (let i = 0; i < arr.length; i++) {
if (arr[pivot] !== target) {
if (target < arr[pivot]) end = pivot;
else start = pivot;
pivot = Math.floor((start + end) / 2);
steps++;
};
if (arr[pivot] === target) return `Found: ${target} in ${steps} steps`;
};
return 'Nothing Found';
};
console.log(linear(unsortedArr, 40)); // Nothing Found
console.log(binary(arr, 44)); // 5 steps in 8 Milliseconds
console.log(binary(arr, 43)); // 2 steps in 7 Milliseconds
Бинарный поиск имеет большой недостаток - он позволяет нам делать это только на отсортированных массивах, но есть и другие решения, основанные на предварительной сортировке данных перед поиском.
Вывод
Это только один из способов применения бинарного поиска, но идея может быть перенастроена для различных структур данных, если они отсортированы. Я надеюсь, что в будущем мы сможем изучить использование этой техники для прохождения более сложных наборов данных на молниеносной скорости ⚡.