13.03.2023 в 10:57

Моделирование парадокса дня рождения с использованием Python

Вы уже испытали на себе парадокс дня рождения. Мы в этом уверены.

Это один из тех парадоксов, которые имеют место в реальной жизни. Вспомните свое время в детском саду, начальной или старшей школе. Или даже подумайте о своей группе друзей. Сколько вы знаете случаев, когда у двух людей был один и тот же день рождения (день и месяц)?

Возможно, Вы даже знаете людей, у которых день рождения совпадает с вашим.

Причина поразительна:

Если в комнате находится по крайней мере 23 человека, то вероятность того, что у двух или более из этих людей день рождения в один и тот же день (без учета года рождения), превышает 50%.

Это определение парадокса дня рождения. В это трудно поверить и все же. Есть 365 дней, но только 23 человека. Как может случиться, что вероятность этого превышает 50%?

Давайте попробуем смоделировать этот парадокс на Python и проведем некоторую визуализацию.

Кодирование парадокса дня рождения

Поскольку день рождения - это один день из 365 дней в году, мы представляем год как дни 1-365 без какого-либо учета месяца.

Чтобы сделать вещи еще более доступными (и короче), позвольте нам представить следующее событие: тот же birthday.

Один и тот же день рождения действителен, если два или более человека из x человек в комнате имеют одинаковый день рождения.

Представление этого статистического события избавляет нас от необходимости писать "два или более человека из..." — и облегчает чтение для вас.

Написание кода довольно простое.

Инициализируйте 23 случайных дня рождения.
Подсчитайте, сколько из них уникальны.
Если уникальных дней менее 23, это означает, что хотя бы один день рождения встречается более одного раза.
Сделайте это несколько раз (например, тысячи раз) для статистической основы.

Вот код:

import numpy as np

# count how often two or more people have the same birthday 
sameBirthday = 0 

iterations = 5000 

for i in range(iterations): 
    # init. array for holding 23 days (birthdays) from 1 - 365 
    birthdays = np.ones(23)
    
    # randomly set one day of the year as birthday 
    for j in range(len(birthdays)): 
        birthdays[j] = np.random.randint(1, 366)
            
    # if there is at least one not-unique birthday, two or more people have the same    
    uniqueBirthdays = len(np.unique(birthdays)) 
  
    if uniqueBirthdays < 23: 
        sameBirthday += 1 

print(sameBirthday / iterations) # about 0.5

Мы видим парадокс, когда выводим соотношение двух или более человек, имеющих одинаковый день рождения, к количеству проведенных экспериментов. Это значение составляет около 0,5. В нашем блокноте это 0,506. Следовательно, вероятность одного и того же дня рождения у 23 человек составляет около 50%.

Закон больших чисел

Возможно, вы уже слышали об этом математическом законе раньше. Закон больших чисел гласит, что чем больше попыток в эксперименте, тем больше усредненный результат будет приближаться к ожидаемому значению. При двукратном подбрасывании монеты ожидаемое значение орла составляет 50%. Тем не менее, поскольку мы подбрасываем монету несколько раз, есть хороший шанс, что мы дважды получим "орел" или "решки".

Подбрасывая монету 1000 раз, мы с гораздо большей вероятностью окажемся в районе ожидаемого значения.

Тот же эффект можно увидеть в парадоксе дня рождения.

Добавив глобальную переменную probByIteration = [] в начало нашего кода, мы можем измерить, как вероятности изменяются с течением времени. Мы можем добавить следующую строку кода в конец нашего цикла (не волнуйтесь, полный код находится в конце):

if (i % 20 == 0) and i > 0:
    probByIteration.append(sameBirthday / i)

Теперь в этом списке указано, как часто одни и те же дни рождения отмечались при разном количестве итераций, с которыми мы экспериментировали. Мы можем легко построить его, используя следующее:

xpoints = list(range(len(probByIteration)))
ypoints = probByIteration

plt.plot(xpoints, ypoints)

plt.xlabel("Iterations")
plt.ylabel("Same birthdays")

plt.show()

И получите этот график:

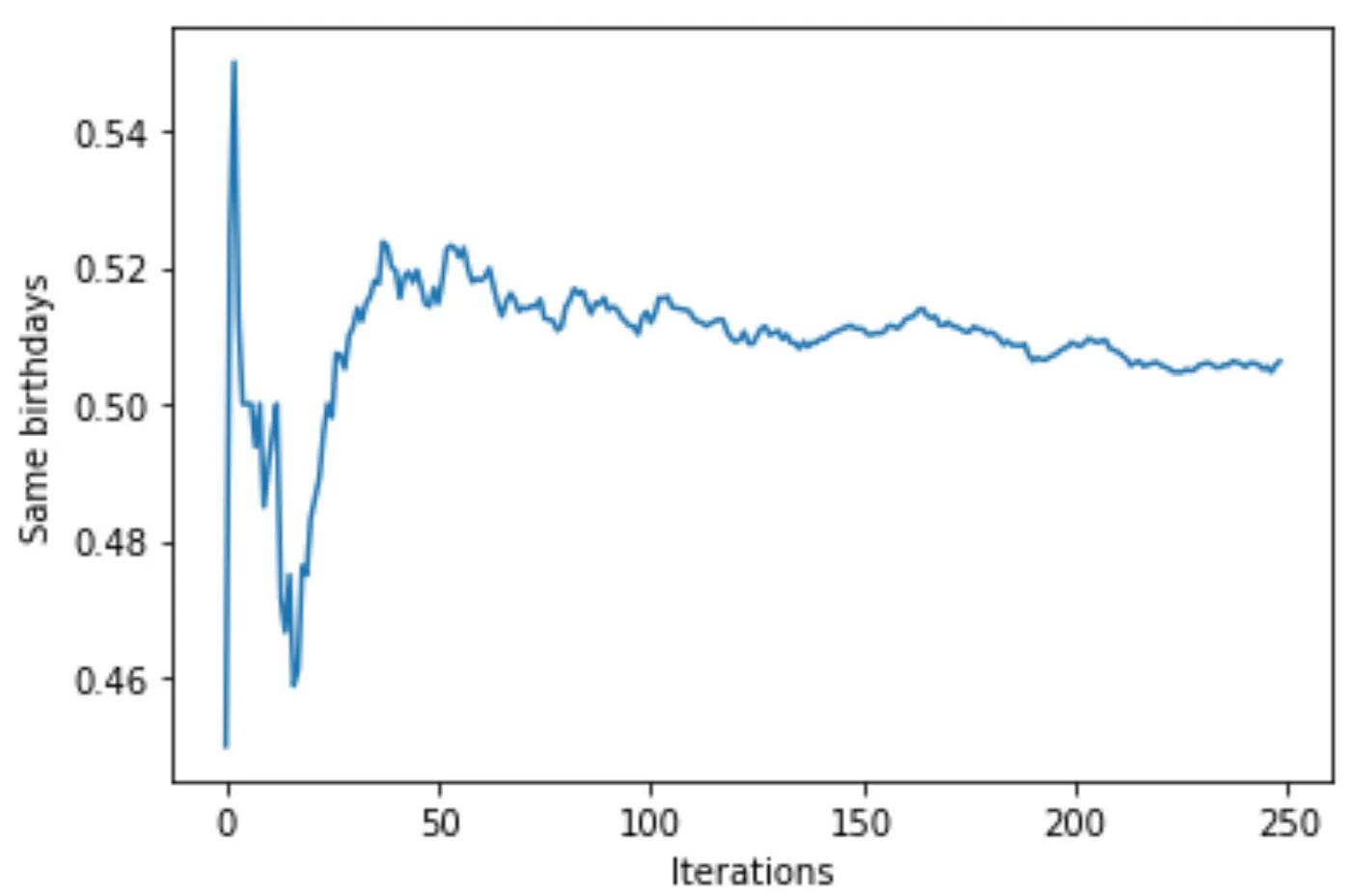
Это закон больших чисел в действии!

Наконец, давайте визуализируем, как и почему вероятность приближается примерно к 50% для разного количества людей. Для нас это самая захватывающая часть.

Чтобы сделать это, мы помещаем наш код в другой цикл, предоставляя другое количество людей.

numsPeople = list(range(2, 24))
probs = []

for numPeople in numsPeople: 
    sameBirthday = 0 
    
    for i in range(iterations): 
        # init. array for holding 23 days (birthdays) from 1 - 365 
        birthdays = np.ones(numPeople)

        # randomly set one day of the year as birthday 
        for j in range(len(birthdays)): 
            birthdays[j] = np.random.randint(1, 366)

        # if there is at least one not-unique birthday, two or more people have the same    
        uniqueBirthdays = len(np.unique(birthdays)) 

        if uniqueBirthdays < numPeople: 
            sameBirthday += 1 
        
    probs.append(sameBirthday / iterations) 


# plotting the probabilities: 
xpoints = numsPeople
ypoints = probs

plt.plot(xpoints, ypoints)

plt.xlabel("Numbers of people in room")
plt.ylabel("Prob. same birthday")

plt.show()

Это приводит нас к следующему графику:

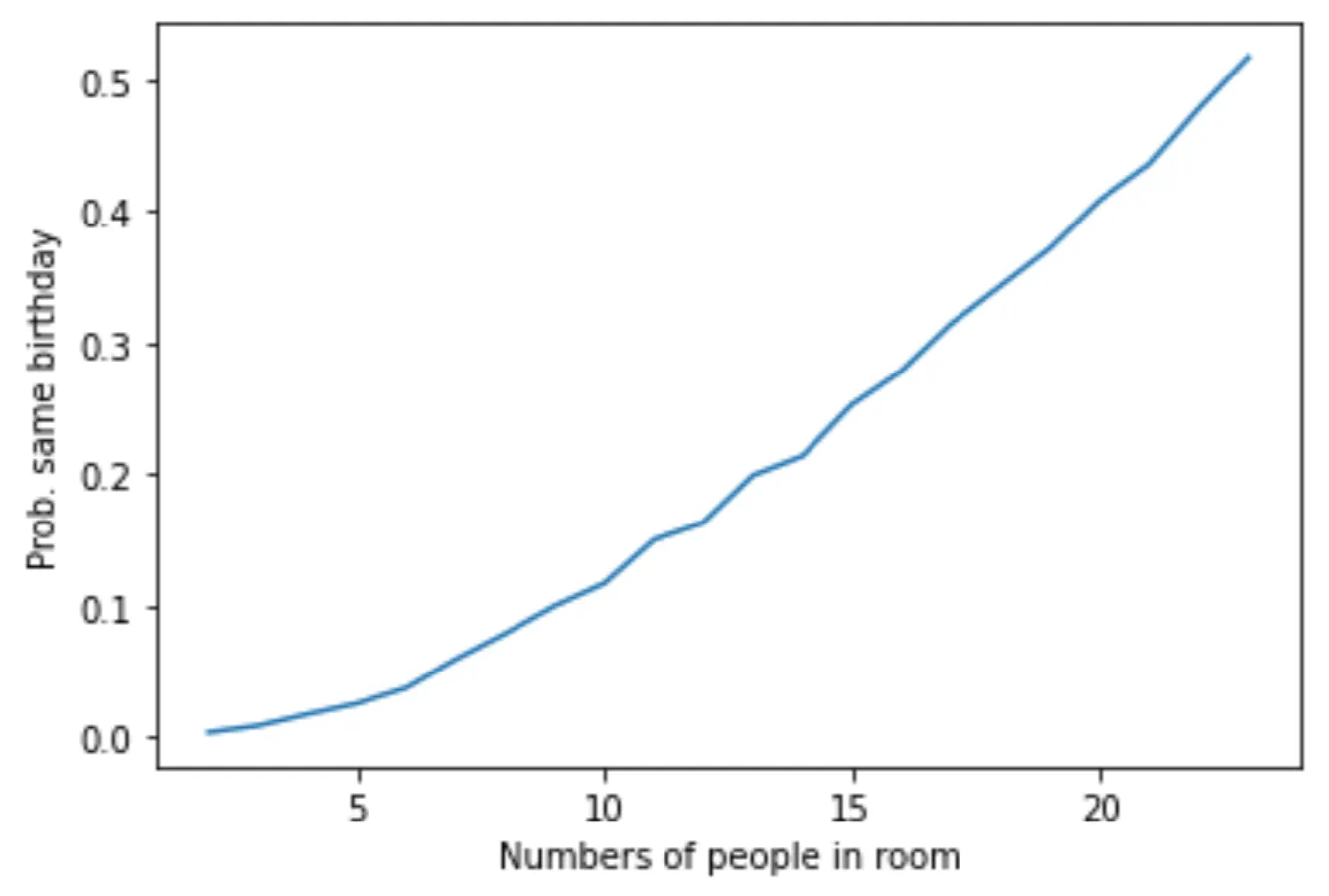
Предоставляем вам полный исходный код на Kaggle.

#Python #Data Science #Matplotlib

314

Войти на сайт

Моделирование парадокса дня рождения с использованием Python

Кодирование парадокса дня рождения

Закон больших чисел