Объяснено с помощью python: Что говорит вам уравнение линейной регрессии?

В этой серии мы внимательно рассмотрим алгоритм машинного обучения и изучим плюсы и минусы каждого алгоритма. Мы рассмотрим алгоритмы вместе с математикой, лежащей в основе алгоритма.
Во-первых, давайте проясним некоторые основные термины, используемые в машинном обучении.
- Контролируемый алгоритм ML: Те алгоритмы, которые используют помеченные данные, известны как контролируемые алгоритмы ml. Контролируемые алгоритмы ml широко используются для двух задач: классификации и регрессии.
- Классификация: Когда задача состоит в том, чтобы классифицировать объекты выборки по определенным категориям (целевая переменная), тогда это называется классификацией. Например, определение того, является ли электронное письмо спамом или нет.
- Регрессия: когда задача состоит в том, чтобы предсказать непрерывную переменную (целевую переменную), тогда это называется регрессией. Например, прогнозирование цен на жилье.
- Неконтролируемый алгоритм ML: те алгоритмы, которые используют немаркированные данные, известны как неконтролируемые алгоритмы ml. Для кластеризации используется неконтролируемый алгоритм.
- Кластеризация: задача поиска групп в заданных немаркированных данных известна как кластеризация.
- Ошибка: разница между фактическим и прогнозируемым значением.
- Градиентный спуск: механизм обновления параметров модели таким образом, чтобы генерировать минимальное значение функции ошибки.
Что такое линейная регрессия в машинном обучении?
Линейная регрессия - это тип контролируемого алгоритма машинного обучения, который используется для прогнозирования непрерывной числовой переменной, известной как цель. Это один из самых простых алгоритмов машинного обучения. Он называется «линейным», потому что алгоритм предполагает, что взаимосвязь между входными характеристиками (также известными как независимые переменные) и выходной переменной (также известной как зависимая или целевая переменная) является линейной. Другими словами, алгоритм пытается найти прямую линию (или гиперплоскость в случае нескольких входных объектов), которая наилучшим образом соответствует данным.
Типы линейной регрессии:
Простая линейная регрессия:
Линейная регрессия известна как простая линейная регрессия, когда прогнозирование выходного значения выполняется с использованием одной входной функции. Мы можем провести линию между зависимыми и независимыми переменными в 2D-пространстве, когда задан один входной признак. здесь b0 — точка пересечения, b1 — коэффициент, x1, x2,…, xn — входные признаки, а y — выходная переменная.
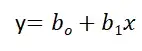
Множественная линейная регрессия:
Линейная регрессия известна как множественная линейная регрессия, когда прогнозирование выходной переменной выполняется с использованием нескольких входных признаков. Мы можем нарисовать плоскость между зависимой и независимой переменными в 3D-пространстве, когда заданы только два входных объекта. В более высоких измерениях визуализация становится затруднительной, но интуиция заключается в том, чтобы найти гиперплоскость в более высоких измерениях. здесь b0 - это перехват, а b1, b2, b3, ......., bn-1, bn известны как коэффициенты, а x1, x2,..., xn известны как входные характеристики, а y - переменная результата.
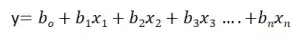
К этому моменту мы поняли, что линейная регрессия пытается построить линейную границу, но как она это делает?
Как он найдет идеальную линию, которая разделяет данные два класса?
Как указано в уравнении, b0 известен как перехват, а b1, b2,...., bn известны как коэффициенты линейной регрессии, и теперь цель состоит в том, чтобы найти ту линейную границу, которая минимизирует функцию ошибки. Функция ошибки представляет собой квадрат суммы разностей между прогнозируемыми и фактическими значениями целевой переменной. Если мы не сведем ошибку в квадрат, то положительные и отрицательные моменты будут компенсировать друг друга.
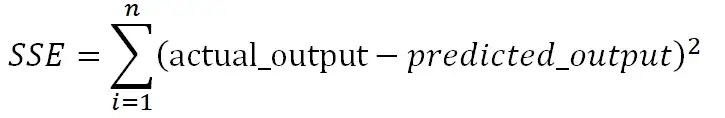
Нам нужно найти коэффициенты и перехваты для линейной регрессии таким образом, чтобы сумма квадратов ошибок (SSE) была минимизирована. Градиентный спуск - один из самых популярных методов, который используется для нахождения оптимальных коэффициентов для ml и алгоритмов глубокого обучения.
В приведенном ниже разделе мы обучим модель на базе данных страхования, где мы должны спрогнозировать расходы с учетом входных данных: возраст, пол, ИМТ, расходы на больницу, количество прошлых консультаций и т.д.
Реализация на Python:
Вы можете использовать библиотеку sklearn на python для обучения и тестирования модели линейной регрессии. Мы будем использовать набор данных insurance.csv для обучения модели линейной регрессии. Некоторые этапы предварительной обработки выполняются для описания данных, обработки пропущенных значений и проверки допущений линейной регрессии.
Шаг 1: Загрузите все необходимые библиотеки и наборы данных, используя библиотеку pandas.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.stats.outliers_influence import variance_inflation_factor as VIF
from sklearn.metrics import classification_report
insurance=pd.read_csv('new_insurance_data.csv')
insurance.head()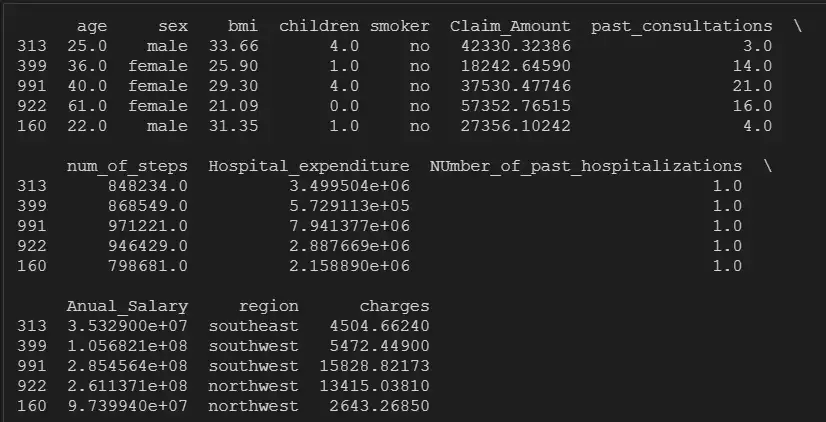
Шаг 2: Проверьте нулевые значения, форму и тип данных переменных:
# checks for non-null entries, size and datatype
insurance.info()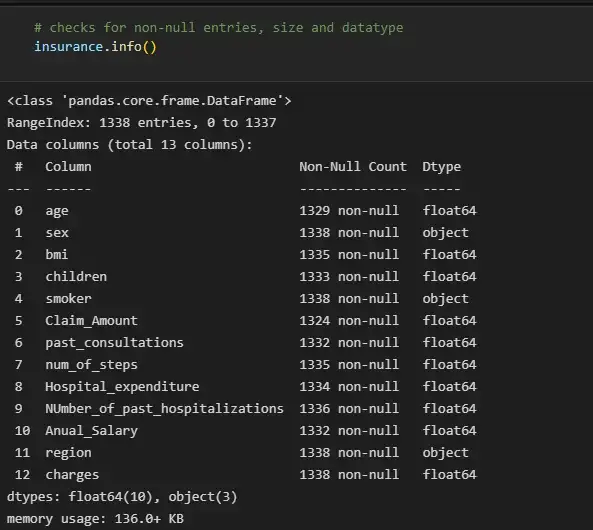
Мы можем отдельно проверить количество нулей для каждой функции, используя df.isna().sum():
insurance.isnull().sum()
# helps me to check for null values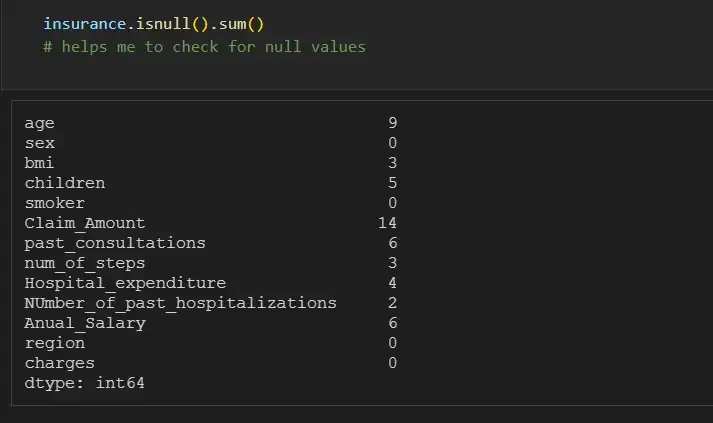
Шаг 3. Заполните пропущенные значения
Мы можем заполнить недостающие значения объектов объектного типа, используя режим, а объектов целочисленного типа - среднее значение или медиану.
# calculating mode for object data type features which will be used to fill missing values.
# We have 3 features which are of object type
print(f"mode of sex feature: {insurance['sex'].mode()[0]}")
print(f"mode of region feature: {insurance['region'].mode()[0]}")
print(f"mode of smoker feature: {insurance['smoker'].mode()[0]}")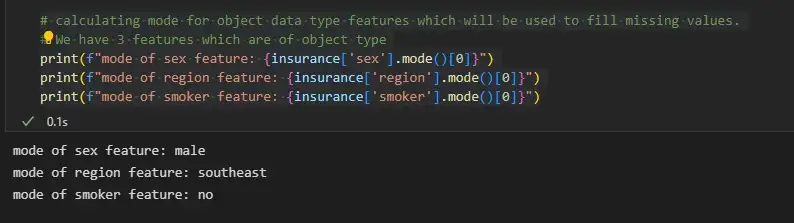
# describe() function will give the descriptive statistics for all numerical features
insurance.describe().transpose()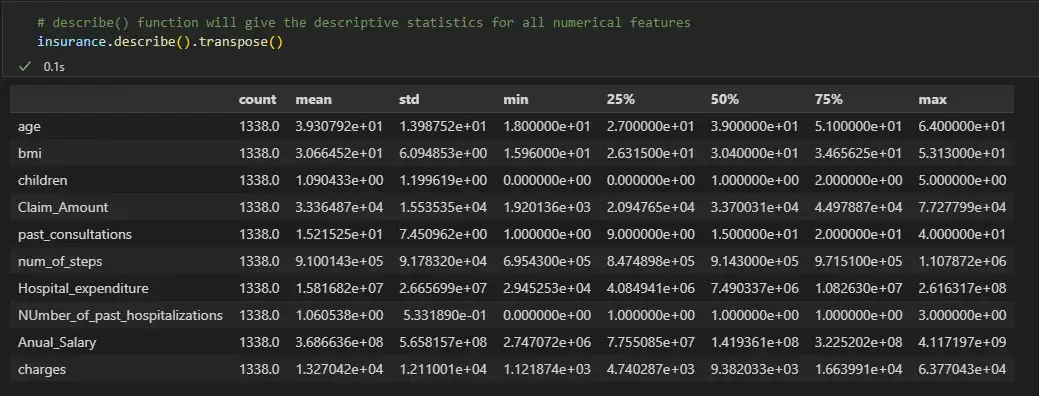
Мы видим, что для числовых признаков среднее и медиана почти одинаковы. Поэтому теперь мы заменим нулевые значения числовых признаков их медианой, а нулевые значения категориальных переменных - их режимом.
for col_name in list(insurance.columns):
if insurance[col_name].dtypes=='object':
# filling null values with mode for object type features
insurance[col_name] = insurance[col_name].fillna(insurance[col_name].mode()[0])
else:
# filling null values with mean for numeric type features
insurance[col_name] = insurance[col_name].fillna(insurance[col_name].median())
# Now the null count for each feature is zero
print("After filling null values:")
print(insurance.isna().sum())
Шаг 4: Анализ выбросов
Мы построим прямоугольную диаграмму для всех числовых характеристик, кроме целевых переменных зарядов.
i = 1
plt.figure(figsize=(16,15))
for col_name in list(insurance.columns):
# total 9 box plots will be plotted, therefore 3*3 grid is taken
if((insurance[col_name].dtypes=='int64' or insurance[col_name].dtypes=='float64') and col_name != 'charges'):
plt.subplot(3,3, i)
plt.boxplot(insurance[col_name])
plt.xlabel(col_name)
plt.ylabel('count')
plt.title(f"Box plot for {col_name}")
i += 1
plt.show()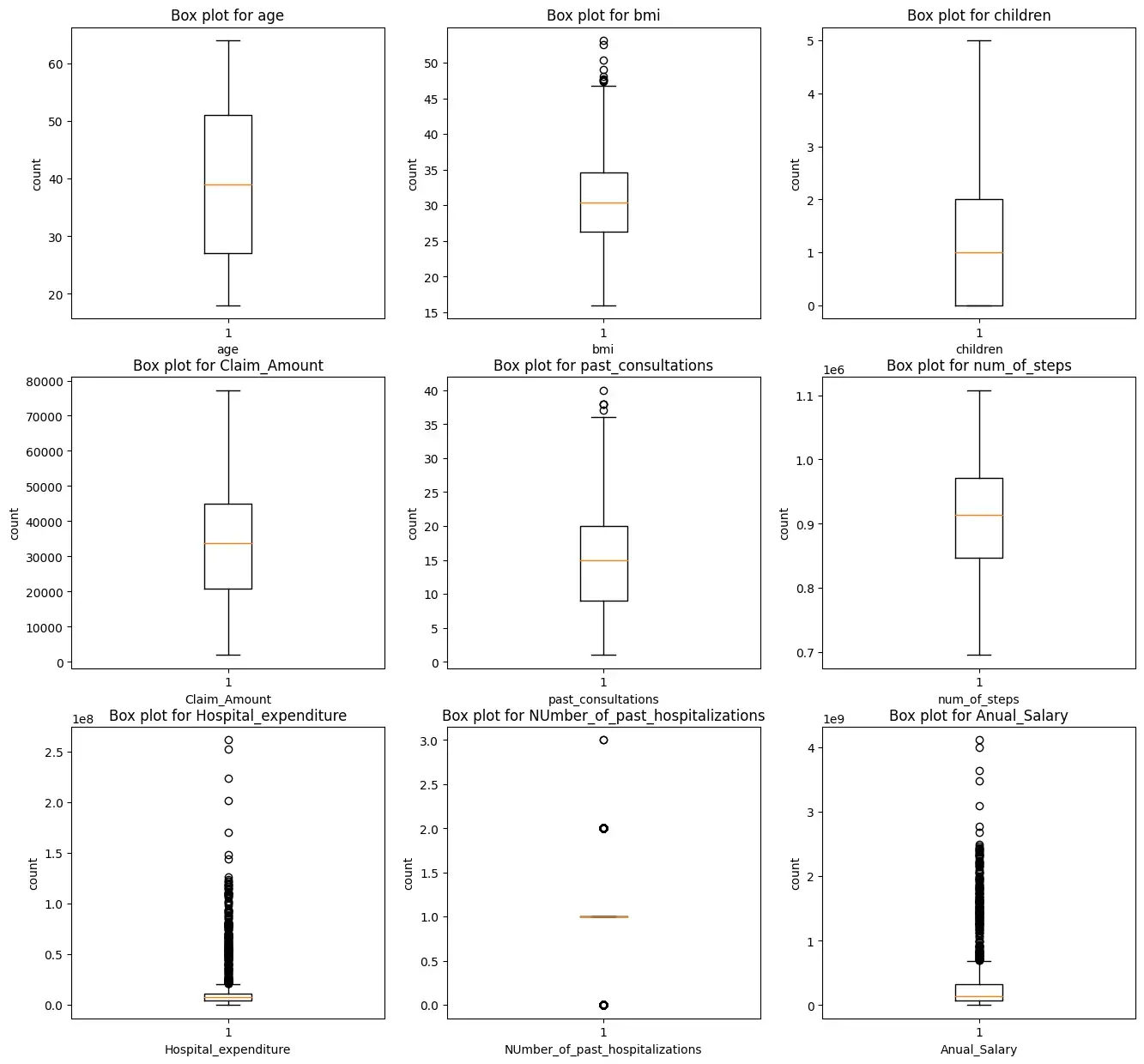
Мы видим, что характеристики ‘bmi’, ‘Hospital_expenditure’ и ‘Number_of_past_hospitalizations’ имеют выбросы. Мы удалим эти выбросы:
outliers_features = ['bmi', 'Hospital_expenditure', 'Anual_Salary', 'past_consultations']
for col_name in outliers_features:
Q3 = insurance[col_name].quantile(0.75)
Q1 = insurance[col_name].quantile(0.25)
IQR = Q3 - Q1
upper_limit = Q3 + 1.5*IQR
lower_limit = Q1 - 1.5*IQR
prev_size = len(insurance)
insurance = insurance[(insurance[col_name] >= lower_limit) & (insurance[col_name] <= upper_limit)]
cur_size = len(insurance)
print(f"dropped {prev_size - cur_size} rows for {col_name} due to presence of outliers")
Шаг 5: Проверьте корреляцию:
Существует корреляция между age & charges, age & Anual_salary и т. д., поскольку их корреляция больше 0,5.
import seaborn as sns
sns.heatmap(insurance.corr(),cmap='gist_rainbow',annot=True)
plt.show()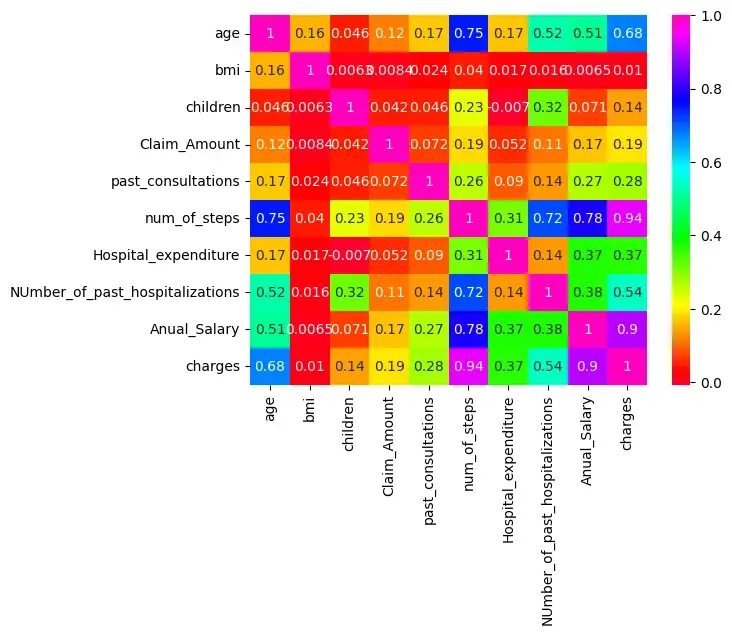
Мы проверим наличие мультиколлинеарности среди признаков:
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)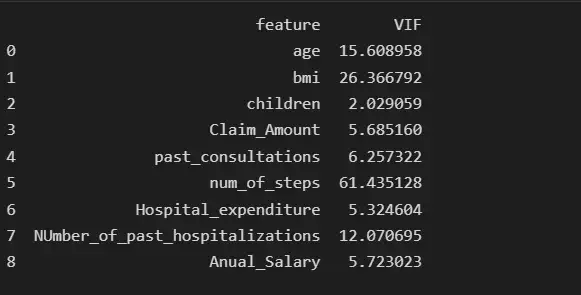
Мы видим, что функция num_of_steps имеет самую высокую коллинеарность, равную 61,43, поэтому мы удалим функцию num_of_steps и снова проверим оценку VIF.
# deleting num_of_steps feature
insurance.drop('num_of_steps', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)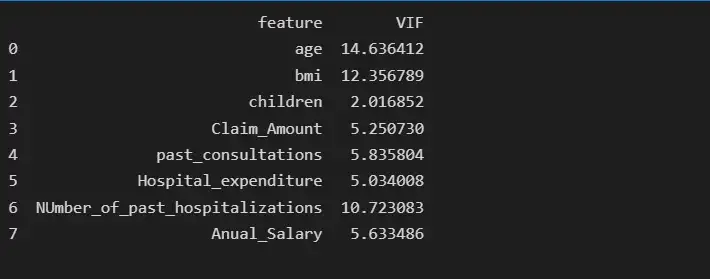
После удаления функции num_of_steps age имеет самую высокую коллинеарность, равную 14,63, поэтому мы удалим функцию age и снова проверим оценку VIF.
# deleting age feature
insurance.drop('age', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)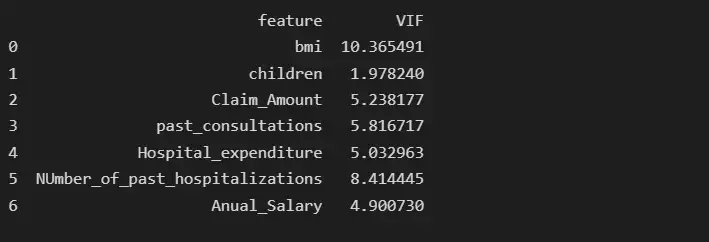
После удаления функции возраста BMI имеет самую высокую коллинеарность, равную 10,36, поэтому мы удалим BMI и снова проверим показатель VIF.
# deleting bmi feature
insurance.drop('bmi', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor
col_list = []
for col in insurance.columns:
if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
col_list.append(col)
X = insurance[col_list]
X = insurance[col_list]
vif_data = pd.DataFrame()
vif_data["feature"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
print(vif_data)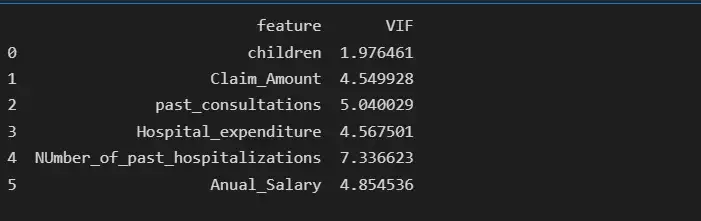
Шаг 6: Разделение входных функций и целевой переменной:
x=insurance.loc[:,['children','Claim_Amount','past_consultations','Hospital_expenditure','NUmber_of_past_hospitalizations','Anual_Salary']]
y=insurance.loc[:,'charges']
x_train, x_test, y_train, y_test=train_test_split(x,y,train_size=0.8, random_state=0)
print("length of train dataset: ",len(x_train) )
print("length of test dataset: ",len(x_test) )
Шаг 7: Обучение модели линейной регрессии на наборе поездов и ее оценка на тестовом наборе данных:
from sklearn.linear_model import LinearRegression
from sklearn.metrics import classification_report, recall_score, r2_score, f1_score, accuracy_score
model = LinearRegression()
# train the model
model.fit(x_train, y_train)
print("trained model coefficients:", model.coef_, " and intercept is: ", model.intercept_)
# model.intercept_ is b0 term in linear boundary equation, and model.coef_ is
# the array of weights assigned to ['children','Claim_Amount','past_consultations','Hospital_expenditure',
# 'NUmber_of_past_hospitalizations','Anual_Salary'] respectively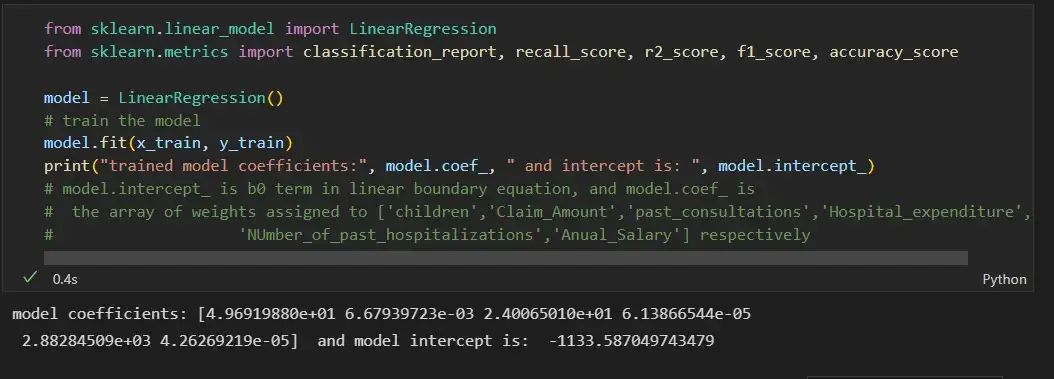
y_pred = model.predict(x_test)
error_pred=pd.DataFrame(columns={'Actual_data','Prediction_data'})
error_pred['Prediction_data'] = y_pred
error_pred['Actual_data'] = y_test
error_pred["error"] = y_test - y_pred
sns.distplot(error_pred['error'])
plt.show()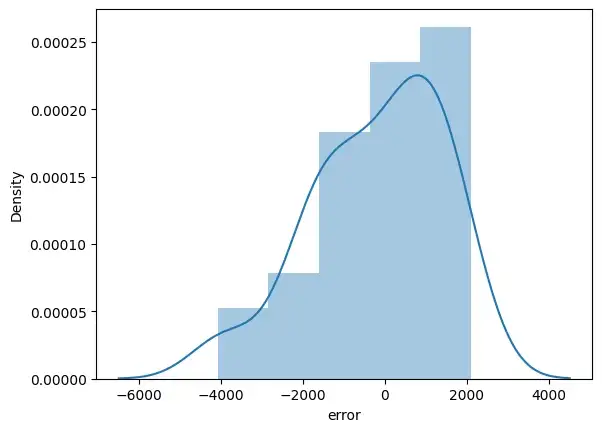
Мы можем построить остаточные графики между фактической целью и остатками или ошибками:
sns.scatterplot(x = y_test,y = (y_test - y_pred), c = 'g', s = 40)
plt.hlines(y = 0, xmin = 0, xmax=20000)
plt.title("residual plot")
plt.xlabel("actural target")
plt.ylabel("residula error")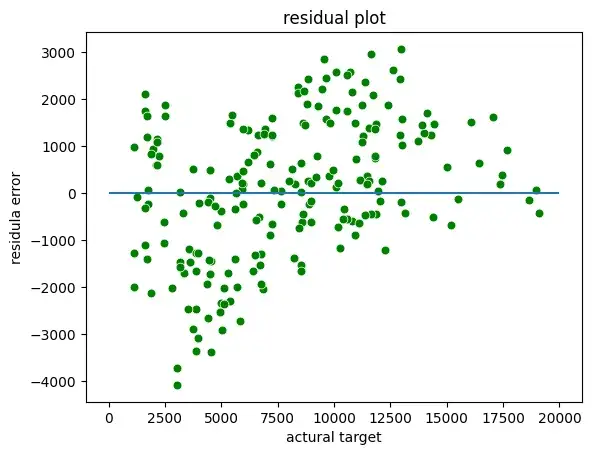
Оценка R-квадрата:
R-квадрат известен как коэффициент детерминации. R Squared — это статистическая мера, которая представляет долю дисперсии зависимой переменной, объясненную независимыми переменными в регрессии. Это значение находится в диапазоне от 0 до 1. Значение «1» указывает, что предиктор полностью учитывает все изменения в Y. Значение «0» указывает, что предиктор «x» не учитывает никаких изменений в «y». Значение R-Squared содержит три термина SSE, SSR и SST.
SSE — это сумма квадратов ошибок. Его также называют остаточной суммой квадратов (RSS).
SSR — это сумма квадратов регрессии.
SST (Сумма в квадрате) — это квадрат разницы между наблюдаемой зависимой переменной и ее средним значением.

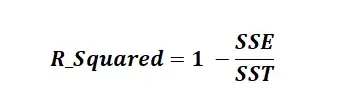
# check for model performance
print(f'r2 score of trained model: {r2_score(y_pred=y_pred, y_true= y_test)}')
Предположения линейной регрессии
- Линейная связь: линейная регрессия предполагает линейную связь между прогнозируемой переменной и независимой переменной. Вы можете использовать точечную диаграмму, чтобы визуализировать взаимосвязь между независимой переменной и зависимой переменной в 2D-пространстве.
- Небольшая мультиколлинеарность или отсутствие мультиколлинеарности между функциями: линейная регрессия предполагает, что функции должны быть независимыми друг от друга, т. Е. Никакой корреляции между функциями. Вы можете использовать функцию VIF, чтобы найти значение мультиколлинеарности признаков. Общее предположение гласит, что если значение признака VIF больше 5, то признаки сильно коррелированы.
- Однородность: линейная регрессия предполагает, что члены ошибок имеют постоянную дисперсию, т. е. разброс членов ошибок должен быть постоянным. Это предположение можно проверить, построив остаточную диаграмму. Если предположение нарушается, то точки образуют форму воронки, в противном случае они будут постоянными.
- Нормальность: линейная регрессия предполагает, что каждая функция данного набора данных следует нормальному распределению. Вы можете строить гистограммы и графики KDE для каждой функции, чтобы проверить, нормально ли они распределены или нет.
- Ошибка: линейная регрессия предполагает, что условия ошибки также должны быть нормально распределены. Вы можете строить гистограммы, а KDE строит графики ошибок, чтобы проверить, нормально ли они распределены или нет.
Вот ссылка GitHub для кода и набора данных.