Проверка гипотезы ANOVA как на R, так и на Python

Дисперсионный анализ (ANOVA) - это набор статистических моделей и связанных с ними процедур оценки, используемых для анализа разницы между средними значениями. ANOVA была разработана статистиком Рональдом Фишером в его статье 1918 года, озаглавленной «Корреляция между родственниками в предположении менделевского наследования», а первое применение ANOVA было опубликовано в 1921 году. ANOVA основан на законе общей дисперсии, где наблюдаемая дисперсия по конкретной переменной разбивается на компоненты, относящиеся к различным источникам вариации. ANOVA обеспечивает статистический тест на то, равны ли два или более средних по совокупности, и, следовательно, обобщает t-критерий за пределы двух средних.

Тест гипотезы ANOVA использует нулевую и альтернативную гипотезы:

• В нулевой гипотезе групповые средние значения равны.
• В альтернативной гипотезе по крайней мере одно среднее значение группы отличается от других групп.
  

В данном примере мы проведем два теста ANOVA как на R, так и на Python. Тест гипотезы, который будет использоваться для ответа на вопросы, - это основанный на дисперсии F-тест, используемый для проверки равенства групповых средних. Сначала приведем код на R, а затем переведем его на Python.

Код на языке программирования R был написан в Reply, который представляет собой бесплатный онлайн-переводчик, поддерживающий различные языки программирования.

Код на языке программирования Python был переведен с помощью Google Colab, который представляет собой бесплатный онлайн Jupyter Notebook, размещенный Google.

Давайте начнем, перед нами несколько сортов риса.

Первый вопрос касается сортов риса. Вопрос исследования:

Влияет ли сорт риса на средний урожай среди этих четырех сортов?

В R встроена функция, aov, которая принимает зависимую переменную и независимую переменную, разнообразие. В этом случае функция aov дала значение p, равное 0,00503, что меньше альфа = 0,05, что означает, что нулевая гипотеза не может быть принята:

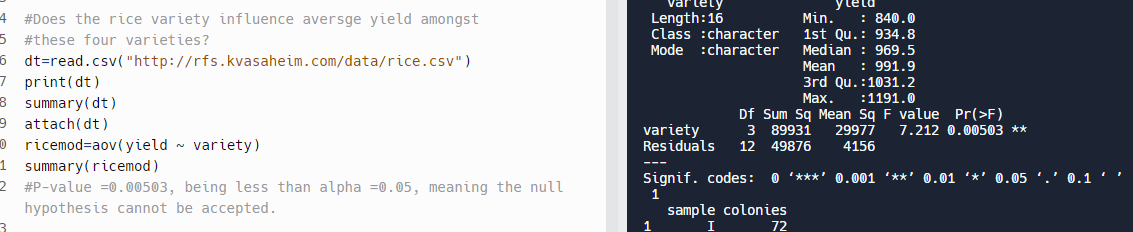
Решить проблему с помощью Python было немного сложнее, потому что фрейм данных нужно было разбить на четыре фрейма меньшего размера для каждого сорта риса. В библиотеке scipy есть функция f_oneway для решения вопроса исследования:

Приведем блочную диаграмму, которая дает визуальное представление о различных сортах риса. Значение p также такое же, как и записанное с использованием R:

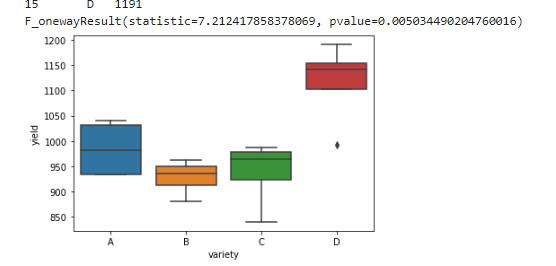
Теперь рассмотрим с другого ракурса - вода в пруду.

Второй пример касается воды в пруду. Исследовательский вопрос заключается в следующем:

Соберите пробу воды из пруда. Разделите эту воду на четыре разных стакана. Разделите выключатели, чтобы убедиться в отсутствии перекрестного загрязнения. Для каждого стакана возьмите четыре образца, подсчитайте и запишите количество амеб.

В R встроена функция aov, которая принимает зависимые колонии и независимую переменную sample. В этом случае функция aov дала значение p, равное 0,669, что больше, чем альфа = 0,05, что означает, что нулевая гипотеза не может быть отклонена:

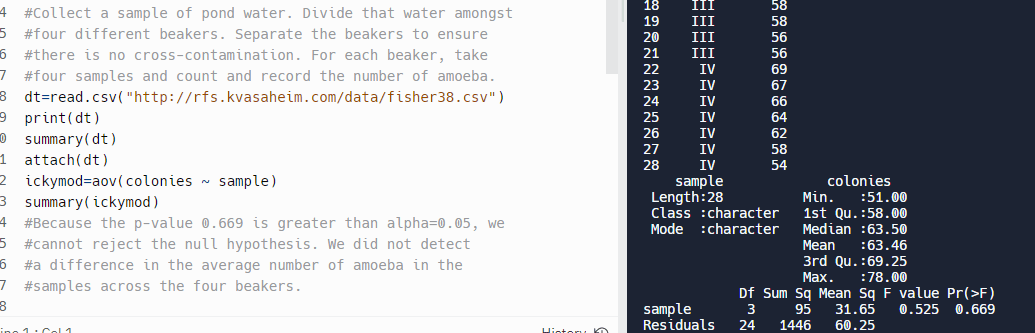
Было немного сложнее решить проблему с помощью Python, потому что фрейм данных нужно было разбить на четыре меньших фрейма данных для каждого образца амебы. В библиотеке scipy есть функция f_oneway для решения вопроса исследования: 

Так же, как и в первом случае, создадим блочную диаграмму, которая дает визуальное представление о различных образцах амебы. Значение p также такое же, как и записанное с использованием R:

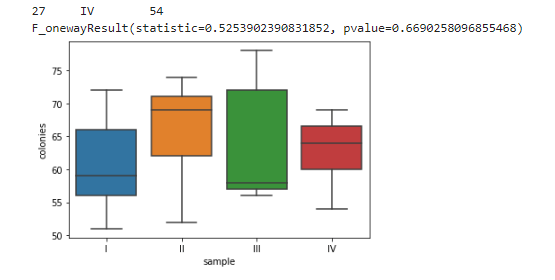
Еще одним интересным моментом является тот факт, что f-статистика обратно пропорциональна p-значению. Следовательно, если p-значение низкое, f-статистика будет высокой, и наоборот.

Мы показали два способа расчета проверки гипотезы ANOVA в R и Python. Python может выполнять те же вычисления, что и R, но для этого требуется больше шагов. Поэтому читателю решать, какой метод ему больше нравится.

На самом деле, некоторые специалисты по данным используют и Python, и R. Они используют Python для своей работы и R для проведения исследований.