Реализация дерева Python с помощью BigTree

Python имеет встроенные структуры данных для списков, массивов и словарей, но не для древовидных структур данных. В LeetCode вопросы для Trees ограничены Binary Search Trees, и его реализация не имеет большого количества функций.

Пакет bigtree Python может создавать и экспортировать деревья в списки Python, словари и DataFrames pandas и из них, легко интегрируясь с существующими рабочими процессами Python.

Древовидные структуры данных можно использовать для отображения иерархических отношений, таких как генеалогические деревья и организационные диаграммы.

В этой статье будут представлены основные понятия дерева, как строить деревья с помощью пакета Python bigtree, методы обхода дерева, поиска, модификации и экспорта. Эта статья заканчивается способами использования деревьев для реализации списка дел и расширения реализации дерева для структур данных Trie и Directed Acycloper Graph.

Основы дерева и терминологии

Tree — это нелинейные структуры данных, которые хранят данные иерархически и состоят из узлов, соединенных ребрами. Например, в генеалогическом дереве узел будет представлять человека, а ребро будет представлять отношения между двумя узлами.

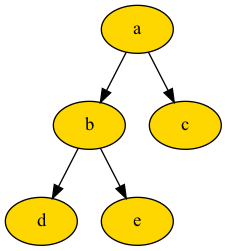
После знакомства с компонентами, составляющими дерево, есть несколько терминов, которые распространяются на эти компоненты.

• Root (Корень): Узел, у которого нет родителя и от которого происходит все дерево. На рис. корень — это узел a.
• Leaf (Лист): узлы, у которых нет дочерних элементов. На рис. конечные узлы — это узлы c, d и e.
  
• Parent Node (Родительский узел): непосредственный предшественник узла. На рис. узел a является родительским узлом для узлов b и c.
  
• Child Node (Дочерний узел): непосредственный преемник узла. На рис. узел b является дочерним узлом узла a.
  
• Ancestors (Предки): все предшественники узла. На рис. узлы a и b являются предками узла d.
  
• Descendants (Потомки): все потомки узла. На рис. узлы d и e являются потомками узла b.
  
• Siblings (Братья и сестры/дети одних родителей): узлы, имеющие одного и того же родителя. На рис. узлы d и e являются братьями и сестрами.
  
• Left Sibling (Левый брат): Брат слева от узла. На рис. узел d является левым братом узла e.
  
• Right Sibling (Правый брат): брат справа от узла. На рис. узел e является правым братом узла d.
  
• Depth (Глубина): длина пути от узла до корня. На рис. глубина узла b равна 2, а узла d — 3.
  
• Height/Max Depth (Высота/максимальная глубина): максимальная глубина от корня до конечного узла. На рис. высота дерева равна 3
  

Настройка Bigtree

Bigtree легко настроить, просто запустите следующую команду в Терминале.

Если вы хотите экспортировать деревья в изображение, вместо этого выполните следующую команду в Терминале.

Давайте погрузимся в реализацию деревьев.

Построение Trees

Чтобы построить деревья, мы должны сначала определить узлы и связать узлы, указав parent и children узла.

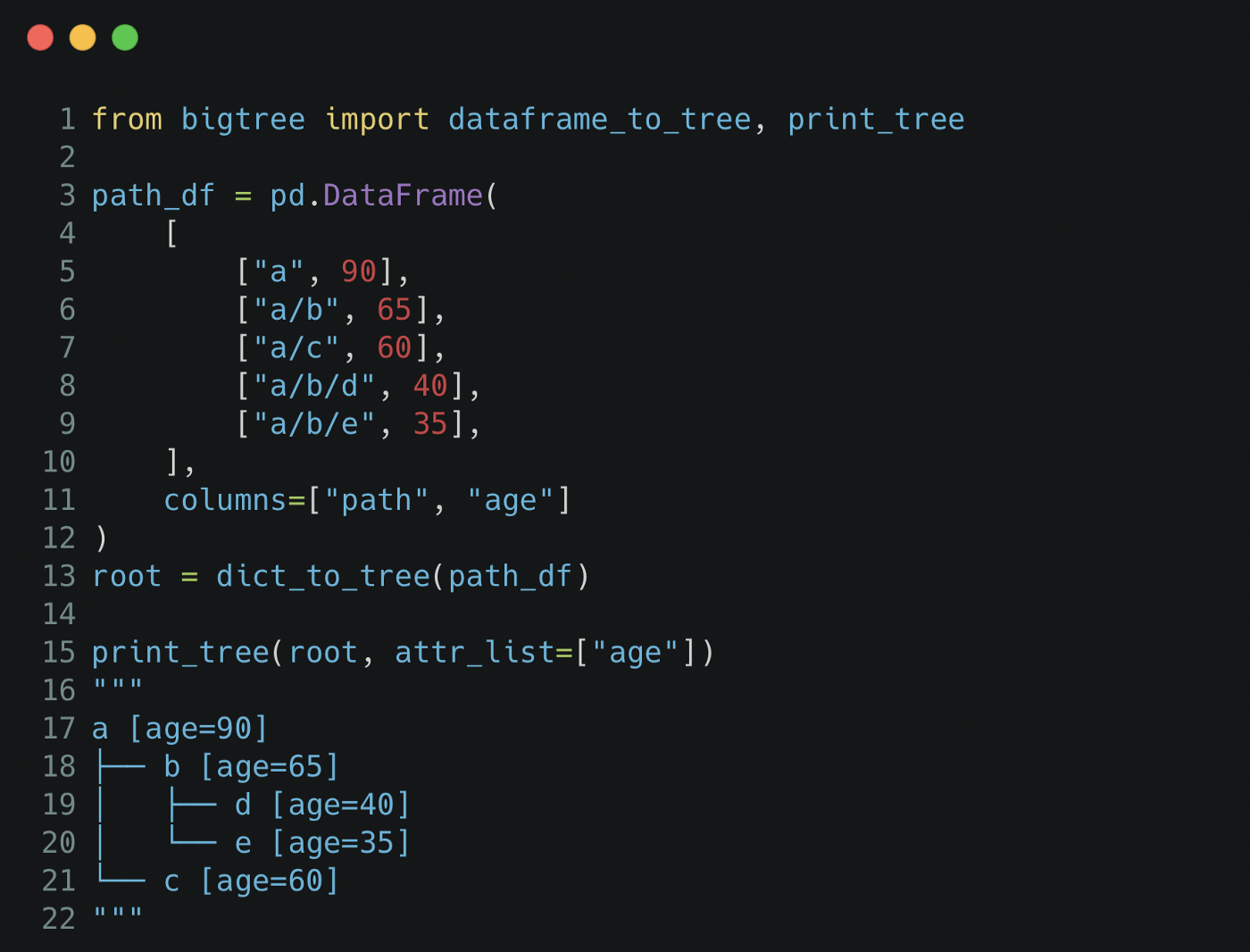
Например, чтобы построить генеалогическое древо,

В приведенном выше примере мы определяем узлы b и c как дочерние элементы узла a с 3 строками кода (строки 3–5). Мы также можем добавить атрибуты, такие как атрибут age, к узлам. Чтобы просмотреть древовидную структуру, мы можем использовать метод print_tree (строка 16).

Мы также можем запросить root, leaves, parent, children, ancestors, descendants, siblings, left_sibling, right_sibling, depth и max_depth узлов, как описано в предыдущем разделе.

Приведенный выше метод определения каждого узла и ребра может быть ручным и утомительным. Существуют альтернативные способы построения деревьев со списками, словарями и пандами DataFrame.

Если нет атрибутов узла, самый простой способ построить дерево — использовать списки Python и метод list_to_tree.

При наличии атрибутов узла рекомендуется построить дерево со словарем или pandas DataFrame, используя методы dict_to_tree и dataframe_to_tree соответственно.

Алгоритмы Tree Traversal

Существует два типа обхода дерева: поиск в глубину (Depth-First Search - DFS) и поиск в ширину (Breadth-First Search - BFS).

• Поиск в глубину (Depth-First Search) начинается с корня и исследует каждую ветвь до конечного узла, прежде чем перейти к следующей ветви.
• Поиск в ширину (Breadth-First Search) начинается с корня и исследует каждый дочерний узел и делает это рекурсивно для каждого узла.
  

 Вы можете подробнее рассмотреть тему в статье Поиск в глубину (Depth-First Search).

Pre-Order Traversal (DFS, NLR)

Pre-Order Traversal — это метод поиска в глубину (DFS), который рекурсивно выполняет 3 шага,

• Посетите текущий узел (N)
• Рекурсивный обход левого поддерева текущего узла (L)
  
• Рекурсивно пройти по правому поддереву текущего узла (R)
  

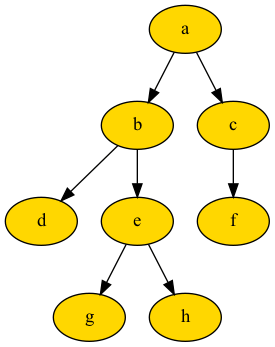
Для обхода в предварительном порядке он будет проходить по дереву на рис. в следующем порядке:

Post-Order Traversal (DFS, LRN)

Post-Order Traversal — это метод поиска в глубину (DFS), который рекурсивно выполняет 3 шага,

• Рекурсивный обход левого поддерева текущего узла (L)
• Рекурсивно пройти по правому поддереву текущего узла (R)
  
• Посетите текущий узел (N)
  

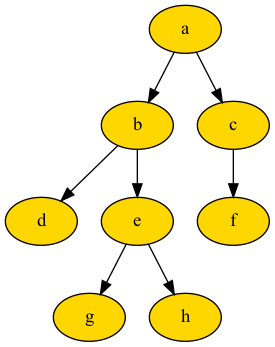
При pre-order traversal он будет проходить по дереву на рис. в следующем порядке:

Level-Order Traversal (BFS)

Level-Order Traversal — это метод поиска в ширину.

При Level-Order Traversal он будет проходить по дереву на рис. в следующем порядке:

Level-Order Group Traversal (BFS)

Level-Order Group Traversal похож на обход по порядку уровней, с той разницей, что каждый уровень будет возвращен как вложенный список; list[idx] обозначает элементы в глубине idx + 1.

Для группового обхода по уровням он будет проходить по дереву на рис. в следующем порядке:

Обратите внимание, что также существует In-Order Traversal (DFS, LNR), который применим только к двоичным деревьям, а не к общим деревьям.

Методы Tree Search

Мы можем использовать методы поиска по дереву, чтобы получить один или несколько узлов, отвечающих определенным критериям, с методами find для одного узла и findall для нескольких узлов.

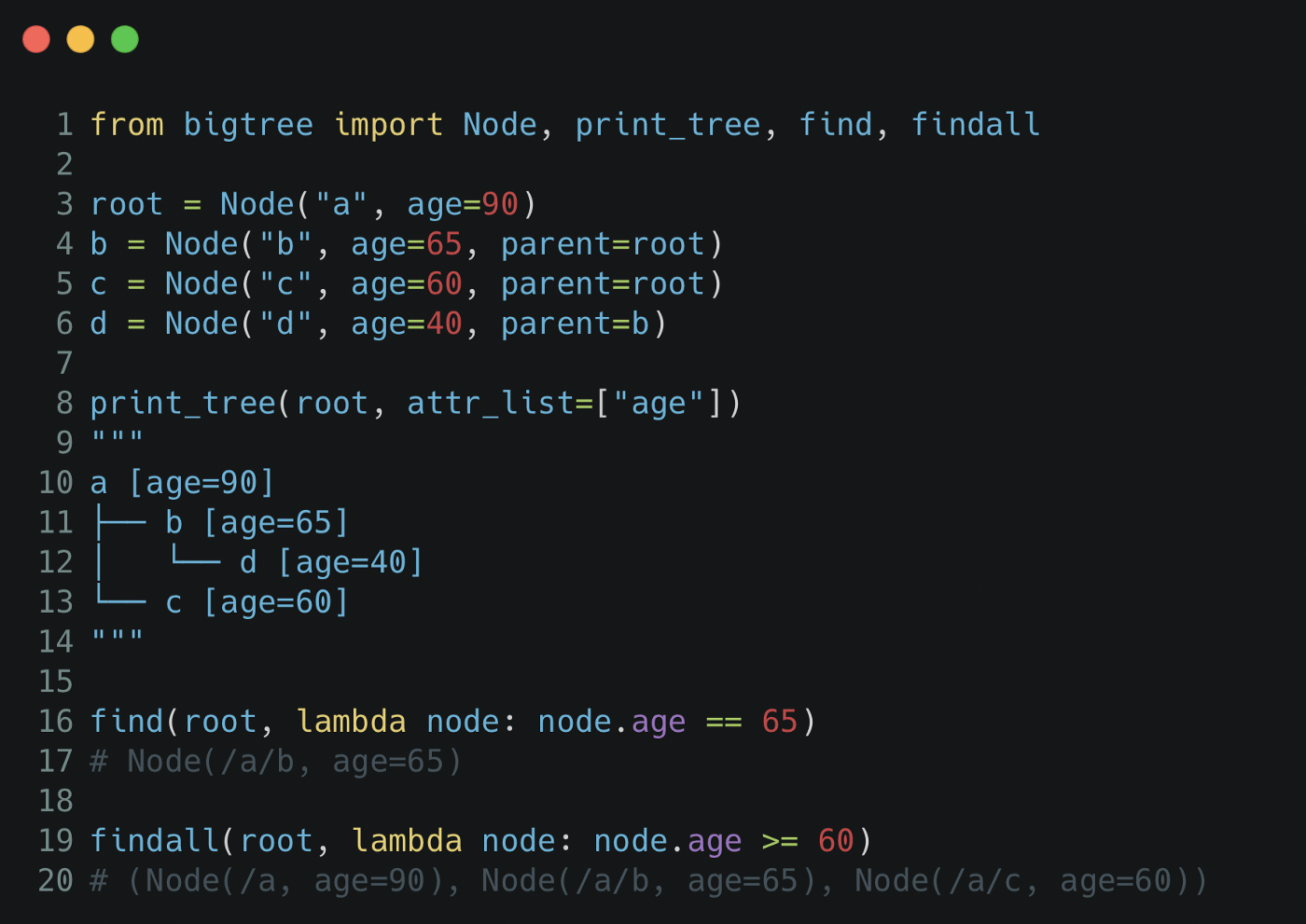
Для общих методов поиска без определения lambda-функции существуют встроенные методы,

• find_attr и find_attrs: найти один/несколько узлов по атрибуту;
• find_name и find_names: найти один/несколько узлов по имени;
  
• find_path, find_paths: найти один/несколько узлов по полному или частичному пути;
  
• find_full_path: найти один узел по их полному пути;
  
• find_children: найти потомков узла по имени, устраняет необходимость поиска по всему дереву.
  

Методы Tree Modification

bigtree поддерживает случаи, когда узлы должны быть перемещены или скопированы из местоположения в место назначения. Например, мы можем перемещать и переупорядочивать узлы в реализации списка дел.

Существуют также другие методы модификации дерева, такие как:

1. copy_nodes: Сделайте копию узла из местоположения в место назначения, узел будет существовать в двух местах.
2. copy_nodes_from_tree_to_tree: Сделайте копию узла из одного дерева в другое дерево, узел будет существовать в двух деревьях.
   

Экспорт Trees

Как упоминалось в начале статьи, bigtree легко интегрируется со словарями Python и пандами DataFrame. Деревья можно экспортировать в словарь, вложенный словарь, Pandas DataFrame и другие форматы.

Печать Tree на консоль

Имея дерево, мы можем вывести дерево на консоль, используя print_tree с возможностью указать атрибуты для печати и стиль дерева. 

Вместо метода генератора вы можете использовать метод yield_tree.

Экспорт Tree в словарь

Имея дерево, мы можем экспортировать дерево в словарь, используя tree_to_dict, с возможностью хранить все атрибуты с именами как есть или сопоставлять атрибуты дерева с именами пользовательских атрибутов с помощью словаря.

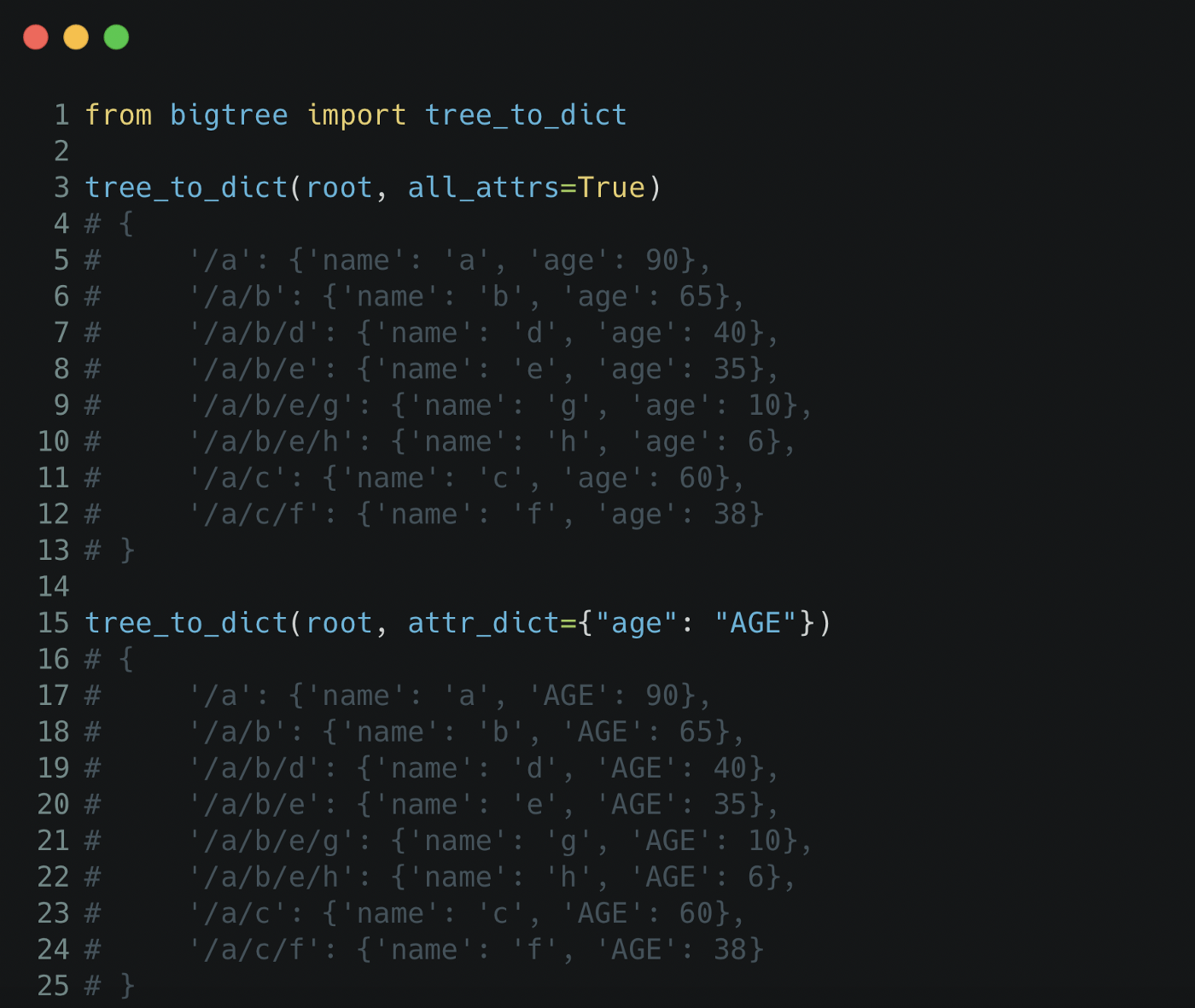
Исходное дерево можно восстановить обратно с помощью метода dict_to_tree.

Экспорт Tree в DataFrame

Имея дерево, мы можем экспортировать дерево в DataFrame, используя tree_to_dataframe с возможностью хранить все атрибуты в виде столбцов с именами как есть или сопоставлять атрибуты дерева с именами пользовательских столбцов с помощью словаря.

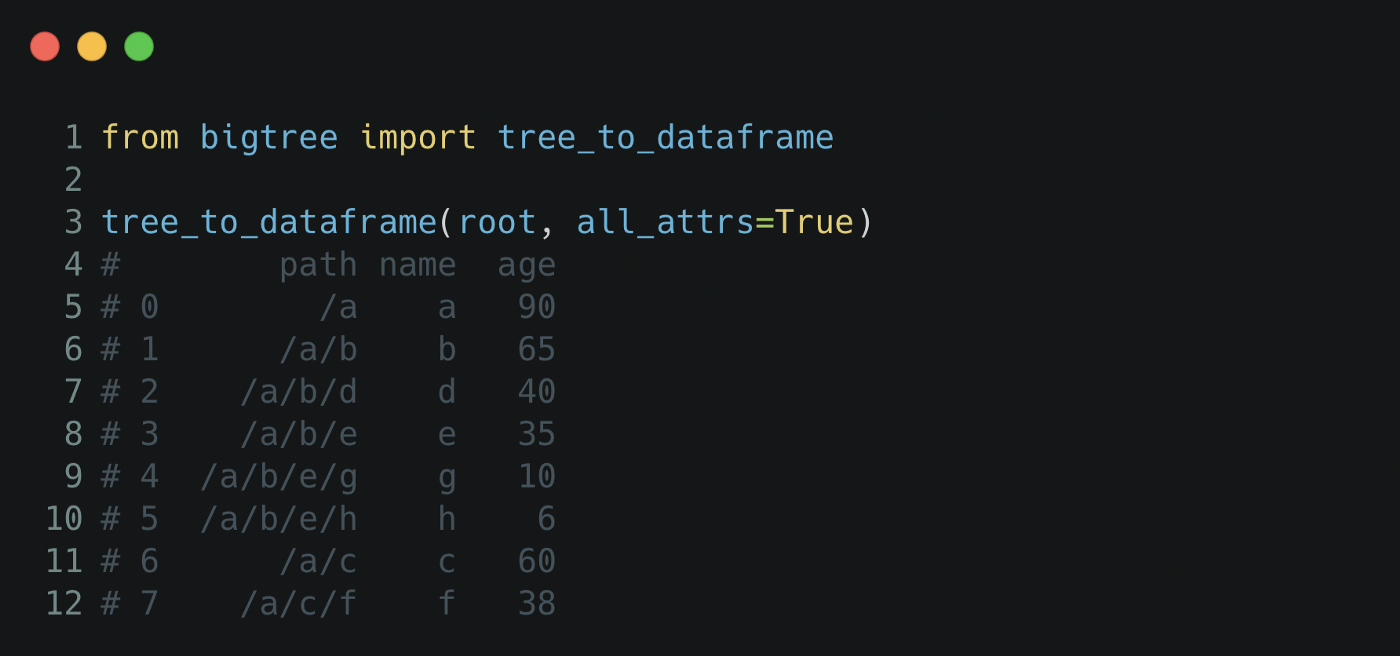
Исходное дерево можно восстановить с помощью метода dataframe_to_tree.

Экспорт Tree в изображение (и многое другое)

Имея дерево, мы можем экспортировать дерево в изображение или другую графику или файлы, используя tree_to_dot. Это использует pydot под капотом, который использует язык Dot и может быть связан с Graphviz.

На рис. экспорт дерева в dot граф имеет тип данных pydot.Dot со встроенной реализацией для записи в форматы файлов dot, PNG, SVG и т. д. Результат аналогичен рис., где приведен пример рассматриваемого дерева.

Дополнительные вохможности bigtree

Использование списка дел с bigtree

Если на данный момент вам все еще интересно, что вы можете сделать с bigtree, bigtree поставляется со встроенным рабочим процессом списка дел с возможностью импорта и экспорта из файла JSON.

Эта реализация списка дел имеет три уровня — имя приложения, имя списка и имя элемента. Вы можете добавлять списки в приложение или добавлять элементы в список. Например,

В приведенном выше примере

1. Название приложения относится к To-Do App;
2. Название списка относится к School, Groceries и General;
   
3. Название предмета относится к Homework 1, Milk, Bread и Cook.
   

Расширение до Trie

Trie — это тип k-арного дерева поиска, используемого для хранения и поиска определенного ключа из набора, полученного из слова reTRIEval. Trie можно использовать для сортировки набора строк в алфавитном порядке или поиска, если для строки присутствует префикс.

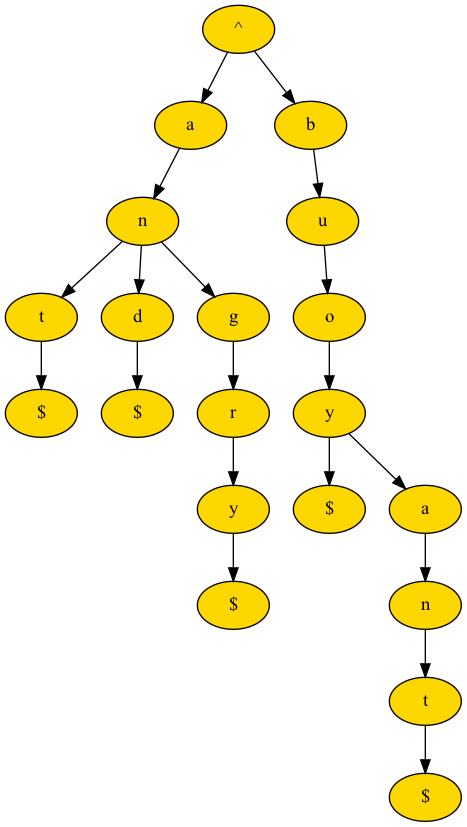
Чтобы расширить bigtree с помощью Trie, мы можем добавить начальный символ ^ и завершающий символ $ к каждому слову и использовать методы поиска по дереву, чтобы найти определенное слово или подслово с помощью find_path. Trie может быть построен как таковой,

Приведенный выше фрагмент кода приводит к изображению на рис., к котором мы привели пример Trie, если экспортировать его с использованием метода tree_to_dot.

Directed Acyclic Graph (DAG)

Направленный ациклический граф (Directed Acyclic Graph - DAG) - это структура данных графа, в которой каждый узел может иметь более одного родителя. Дерево считается ограниченной формой графа. Это различие приводит к следующим различиям,

• Root: В DAG нет концепции корня, поскольку узел может иметь несколько родителей.
• Depth: В DAG нет понятия глубины, так как нет корневого узла.
  
• Height/Max depth: В DAG нет понятия высоты, так как нет корневого узла.
  

DAG лучше всего использовать для представления рабочих процессов, поскольку рабочие процессы имеют определенный порядок (направленный) и не повторяются бесконечно; не имеет петель (ациклический).

Подобно деревьям, DAG в bigtree можно создавать вручную из списков Python, словарей или фреймов данных pandas с помощью методов list_to_dag, dict_to_dag и dataframe_to_dag соответственно.

Приведенный выше фрагмент кода приводит к следующему изображению:

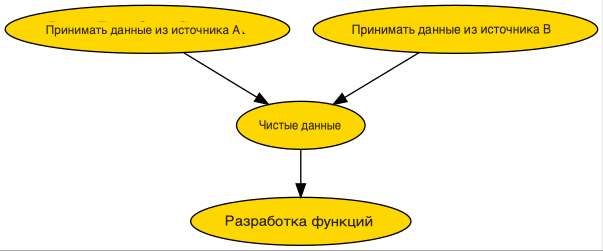
Надеюсь, вы лучше разобрались в древовидных структурах и в том, как их реализовать с помощью пакета bigtree Python.