Сжатие изображения - метод DCT
Мы видим, что в последние годы наблюдается экспоненциальный рост вычислительных ресурсов и данных. Хотя и вычислительные ресурсы, и объем данных растут, темпы роста этих же показателей резко отличаются. Теперь у нас очень большие объемы данных и недостаточно вычислительных ресурсов для их обработки в приличное количество времени. Это подводит нас к одной из основных проблем, с которыми мир сталкивается сейчас. Как мы можем сжимать информацию о данных, сохраняя при этом большую часть информации, содержащейся в данных?
В этом проекте мы будем иметь дело с информацией об изображении. К изображениям применяются два основных типа сжатия - сжатие без потерь и сжатие с потерями. Некоторыми примерами стандартов сжатия без потерь являются PNG (переносимая сетевая графика) и PCX (обмен изображениями). При сжатии без потерь вся информация сохраняется, но степень сжатия низкая. Если нам нужно более высокое сжатие, мы должны рассмотреть алгоритмы сжатия с потерями. Одним из широко используемых алгоритмов сжатия с потерями является алгоритм сжатия JPEG. Алгоритм JPEG работает на DCT, что является темой обсуждения в этом проекте.
DCT расшифровывается как Discrete Cosine Transform. Это тип быстрого вычисления преобразования Фурье, который отображает реальные сигналы в соответствующие значения в частотной области. DCT работает только с реальной частью сложного сигнала, потому что большинство реальных сигналов являются реальными сигналами без сложных компонентов. Здесь мы обсудим реализацию алгоритма DCT для данных изображения и его потенциальное использование. Проект размещен на GitHub, и вы можете просмотреть его здесь.
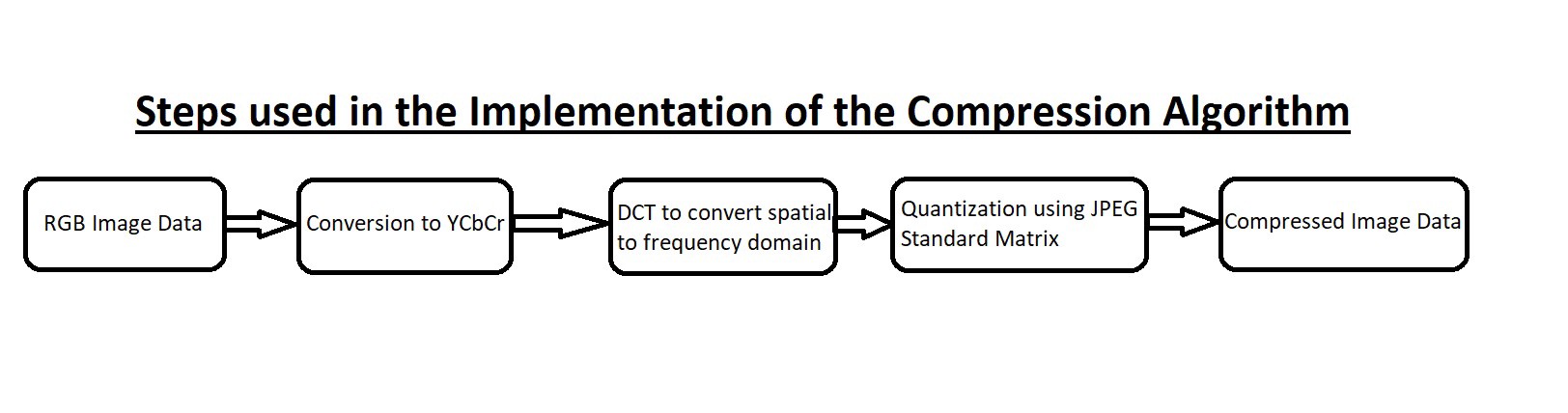
Этапы реализации DCT для сжатия изображений:
· Если у нас есть многоканальное изображение, нам нужно применить алгоритм индивидуально к каждому каналу. Мы должны преобразовать изображение RGB в эквивалентный формат YCbCr, прежде чем сможем выполнять обработку DCT. Другим важным шагом здесь является изменение диапазона значений пикселей с -128 до 127 вместо 0 до 255, что является стандартным диапазоном значений для 8-битных изображений.
BGRImage = cv2.imread('/content/nature1.jpg')
BGRImage = cv2.resize(BGRImage, (800, 1200))
YCrCbImage = cv2.cvtColor(BGRImage, cv2.COLOR_BGR2YCR_CB)
Y, Cb, Cr = YCrCbImage[:,:,0], YCrCbImage[:,:,1], YCrCbImage[:,:,2]
Y = np.array(Y).astype(np.int16)
Cb = np.array(Cb).astype(np.int16)
Cr = np.array(Cr).astype(np.int16)
Y, Cb, Cr = Y - 128, Cb - 128, Cr - 128
· Изображение разбито на N * N блоков. Здесь мы берем N = 8, потому что это стандарт алгоритма JPEG.
· Затем DCT последовательно применяется к каждому блоку.
· Квантование применяется для ограничения количества значений, которые могут быть сохранены без потери информации.
· Подмножество квантованных блоков сохраняется в массиве, откуда его можно взять для дальнейшей обработки.
· Мы можем применить IDCT к квантованным блокам, а затем расположить блоки 8 * 8 в последовательном порядке, чтобы получить изображение YCbCr, которое затем можно преобразовать в RGB, чтобы получить исходное изображение в сжатой форме. Этот шаг не был реализован в рамках данного проекта.
Реализация алгоритма сжатия изображения:
Уравнение DCT для 2D DCT показано на изображении ниже. P(x, y) здесь обозначает пиксели входного изображения.

Однако, когда мы имеем дело со сжатием JPEG, мы всегда берем N = 8, что изменяет уравнение и дает нам уравнение ниже:
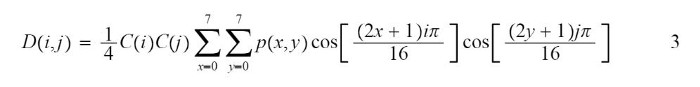
Но применение этого сложного скалярного вычисления в каждой точке блока изображения 8 * 8 может занять много времени, поэтому мы можем дополнительно упростить уравнения, чтобы получить их векторное представление. Векторное представление того же самого может быть дано следующим образом:
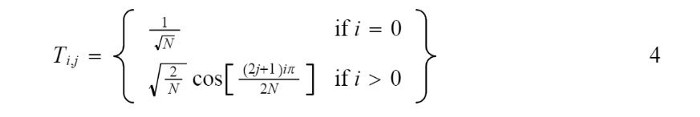
Мы вычисляем DCT, применяя следующую формулу -
D = DCT_Matrix @ Image_Block @ DCT_Matrix.T
Блок квантования для 8 * 8 DCT закодирован непосредственно в функцию. Однако пользователь может выбрать необходимую степень сжатия в соответствии с дальнейшим применением.
Человеческая зрительная система более восприимчива к низкочастотным компонентам изображения по сравнению с высокочастотными компонентами. Следовательно, мы можем легко отбросить высокочастотные компоненты из изображения и по-прежнему сохранить большую часть информационного содержания в изображении. После квантования обработанный массив размером 8 * 8 может быть уменьшен до более низкого измерения. Здесь мы берем подмножество блока 5 * 5, которое по-прежнему сохраняет около 95% информации, при этом уменьшая размер на 60,9% (1 - (25/64)). Это также помогает нам достичь общей степени сжатия от 60% до 67% в зависимости от размера входного изображения.
Результаты эксперимента:
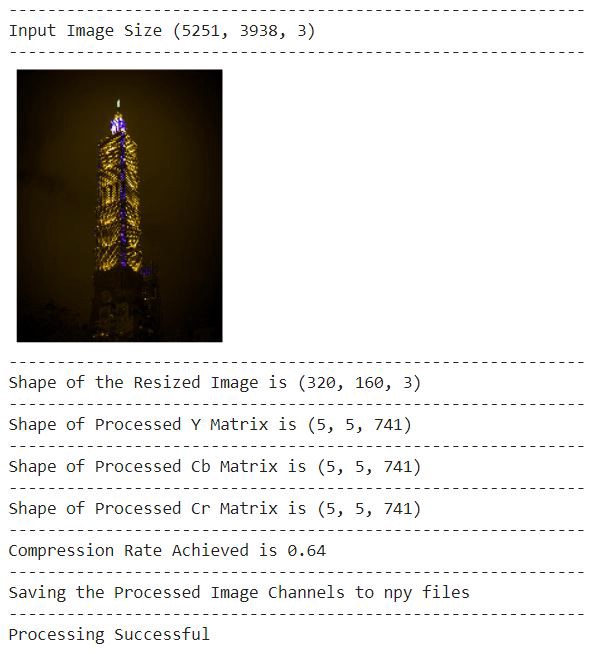

Приложения:
· Изображения могут быть сохранены в сжатом формате и могут быть повторно преобразованы в версию RGB, когда они должны отображаться.
· Обработанные блоки информации могут быть отправлены по каналу связи, что потребляет меньшую полосу пропускания.
· Эта обработанная информация DCT может быть предоставлена в качестве входных данных для задач компьютерного зрения на основе глубокого обучения, которые обычно требуют большого количества высококачественных данных.
Как специалист по анализу данных, имеющий опыт работы в области электроники и телекоммуникаций, который в основном сосредоточился на обработке сигналов, я видел и работал с первыми двумя частями, упомянутыми в разделе приложений. Моя цель в конечном итоге - реализовать третью часть сейчас.