09.11.2022 в 17:54

Тематическое моделирование с использованием LDA

О чем говорят страны на Общих дебатах ООН? Здесь мы рассмотрим интуицию, лежащую в основе LDA, и ее ограничения, а также реализацию на python с использованием Gensim.

Что такое скрытое распределение Дирихле (Latent Dirichlet Allocation)?

Скрытое распределение Дирихле (LDA) - популярная модель, когда речь идет об анализе больших объемов текста. Это генеративная вероятностная модель, которая позволяет пользователям обнаруживать скрытые («латентные») темы из коллекции документов. LDA моделирует каждый документ как созданный в процессе многократной выборки слов и тем из статистических распределений. Применяя умные алгоритмы, LDA может восстановить наиболее вероятные распределения, которые использовались в этом генеративном процессе (Blei, 2003). Эти дистрибутивы рассказывают нам кое-что о том, какие темы существуют и как они распределены между каждым документом.

Давайте сначала рассмотрим простой пример, иллюстрирующий некоторые ключевые особенности LDA. Представьте, что у нас есть следующая коллекция из 5 документов

🍕🍕🍕🍕🍕🦞🦞🦞🐍🐍🐋🐋🐢🐌🍅
🐌🐌🐌🐌🐍🐍🐍🐋🐋🐋🦜🦜🐬🐢🐊
🐋🐋🐋🐋🐋🐋🐢🐢🐢🐌🐌🐌🐍🐊🍕
🍭🍭🍭🍭🍭🍭🍕🍕🍕🍕🍅🍅🦞🐍🐋
🐋🐋🐋🐋🐋🐋🐋🐌🐌🐌🐌🐌🐍🐍🐢

и хотите понять, какие темы присутствуют и как они распределяются между документами. Быстрое наблюдение показывает, что у нас много смайликов, связанных с едой и животными

еда: {🍕,🍅,🍭,🦞}
животные: {🦞🐍🐋🐬🐌🦜}

и что эти темы проявляются в разных пропорциях в каждом документе. Документ 4 в основном посвящен еде, документ 5 в основном - животным, а первые три документа представляют собой смесь этих тем. Это то, что мы имеем в виду, когда говорим о распределении тем, доля тем распределена по разному в каждом документе. Кроме того, мы видим, что смайлики 🐋 и 🍭 появляются чаще, чем другие смайлики. Это то, что мы имеем в виду, когда говорим о распределении слов по каждой теме.

Эти раздачи по темам и словам в каждой теме - это то, что возвращает нам LDA. В приведенном выше примере мы пометили каждую тему как еда и животное, чем LDA, к сожалению, не занимается для нас, Он просто возвращает нам распределение слов для каждой темы, из которого мы, как пользователи, должны сделать вывод о том, что на самом деле означает тема.

Итак, как LDA обеспечивает распределение слов по каждой теме? Как уже упоминалось, предполагалось, что каждый документ создается случайным процессом рисования тем и слов из различных дистрибутивов, и используется умный алгоритм для поиска параметров, которые являются наиболее вероятными параметрами для получения данных.

Интуиция, стоящая за LDA

LDA - это вероятностная модель, которая использует как Дирихле, так и мультиномиальные распределения. Прежде чем мы продолжим с подробностями того, как LDA использует эти дистрибутивы, давайте сделаем небольшой перерыв, чтобы освежить в памяти, что означают эти дистрибутивы. Распределения Дирихле и мультиномиальные распределения являются обобщениями бета- и биномиальных распределений. В то время как бета- и биномиальные распределения можно понимать как случайные процессы, связанные с подбрасыванием монет (возвращением дискретного значения), Дирихле и мультиномиальные распределения имеют дело со случайными процессами, связанными, например, с бросанием костей. Итак, давайте сделаем шаг назад и рассмотрим несколько более простой набор распределений: бета-распределение и биномиальное распределение.

Бета- и биномиальное распределение

LDA — это вероятностная модель, в которой используются как распределения Дирихле, так и полиномиальные распределения. Прежде чем мы продолжим подробно рассказывать о том, как LDA использует эти дистрибутивы, давайте сделаем небольшой перерыв, чтобы освежить нашу память о том, что означают эти дистрибутивы. Распределения Дирихле и мультиномиальные распределения являются обобщениями бета-распределений и биномиальных распределений. В то время как бета-и биномиальные распределения можно понимать как случайные процессы, включающие подбрасывание монет (возвращающие дискретное значение), распределения Дирихле и мультиномиальные распределения имеют дело со случайными процессами, касающимися, например, бросание игральных костей. Итак, давайте сделаем шаг назад и рассмотрим несколько более простой набор распределений: бета-распределение и биномиальное распределение. Для простоты мы будем использовать пример подбрасывания монеты, чтобы проиллюстрировать, как работает LDA. Представьте, что у нас есть документ, полностью написанный всего двумя словами: 🍕 и 🍅, и этот документ создается путем многократного подбрасывания монеты. Каждый раз, когда монета падает орлом, мы пишем 🍕, и каждый раз, когда монета падает решкой, мы пишем 🍅. Если мы заранее знаем, каков уклон монеты, другими словами, какова вероятность того, что она выдаст 🍕, мы можем смоделировать процесс генерации документа с помощью биномиального распределения. Например, вероятность получения 🍕🍕🍕🍕🍕🍕🍕🍅🍅🍅 (в любом порядке) определяется как P = 120P(🍕)⁷P(🍅)³, где 120 — количество комбинаций, позволяющих расположить 7 пицц и 3 помидора.

Но как мы узнаем вероятности P(🍕) и P(🍅)? Учитывая приведенный выше документ, мы могли бы оценить P (🍕) = 7/10 и P (🍅) = 3/10, но насколько мы уверены в присвоении этих вероятностей? Подбрасывание монеты 100 или даже 1000 раз еще больше сузило бы эти вероятности.

В приведенном выше эксперименте каждый эксперимент дал бы нам одинаковую вероятность P (🍕) = 7/10 = 0,7. Однако каждый последующий эксперимент укреплял нашу уверенность в том, что P(🍕)=7/10. Именно бета-распределение дает нам возможность количественно оценить укрепление наших убеждений после получения дополнительных доказательств. Бета-распределение принимает два параметра 𝛼 и 𝛽 и создает распределение вероятностей. Параметры 𝛼 и 𝛽 можно рассматривать как «псевдосчетчики» и они представляют, сколько предварительных знаний мы имеем о монете. Более низкие значения 𝛼 и 𝛽 приводят к более широкому распределению и отражают неопределенность и отсутствие предварительных знаний. С другой стороны, большие значения 𝛼 и 𝛽 дают распределение с резким пиком около определенного значения (например, 0,7 в третьем эксперименте). Это означает, что мы можем подтвердить наше утверждение о том, что P(🍕)=0,7. Мы иллюстрируем бета-распределение, соответствующее трем вышеупомянутым экспериментам, на рисунке ниже.

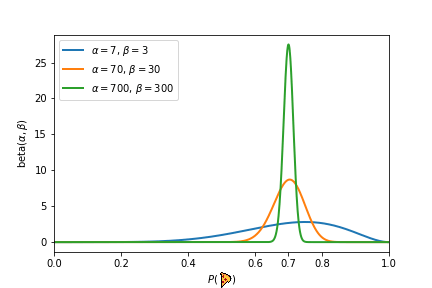
Бета-распределение с различными значениями альфа и бета-версии. Большое количество экспериментов означает более узкий разброс.

Теперь подумайте об этом таким образом, у нас есть априорное убеждение, что вероятность приземления головой равна 0,7. Это наша гипотеза. Вы продолжаете другой эксперимент — подбрасываете монету 100 раз и получаете 74 орла и 26 решек, какова вероятность того, что априорная вероятность, равная 0,7, верна? Томас Байес обнаружил, что вы можете описать вероятность события на основе априорных знаний, которые могут быть связаны с событием, с помощью теоремы Байеса, которая показывает, как с учетом некоторой вероятности, гипотезы и доказательств мы можем получить апостериорную вероятность:

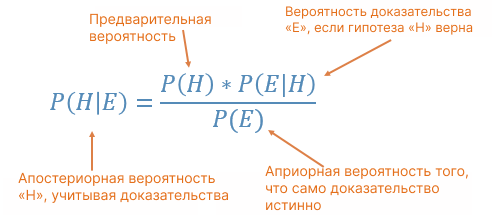
Здесь есть 4 компонента:

Априорная вероятность: гипотеза или априорная вероятность. Он определяет наши прежние убеждения о событии. Идея состоит в том, что мы предполагаем некоторое априорное распределение, наиболее разумное с учетом наших лучших знаний. Априорная вероятность — это P (голова) каждой монеты, сгенерированная с использованием бета-распределения, которая в нашем примере равна 0,7.
Апостериорная вероятность: вероятность априорной вероятности с учетом свидетельства. Это вероятность вероятности. Учитывая 100 подбрасываний с 74 орлами и 26 решками, какова вероятность того, что априорная вероятность, равная 0,7, верна? Другими словами, при наличии свидетельств/наблюденных данных какова вероятность того, что предыдущее убеждение верно?
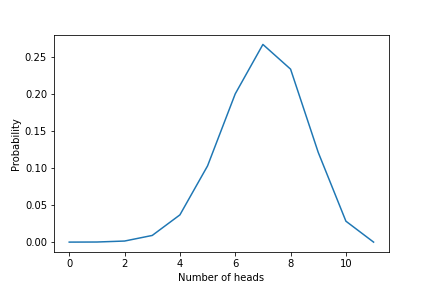
Вероятность: вероятность может быть описана как вероятность наблюдения данных/доказательств при условии, что наша гипотеза верна. Например, предположим, что я подбросил монету 100 раз и получил 70 орлов и 30 решек. Учитывая наше предыдущее убеждение, что P (орел) равен 0,7, какова вероятность наблюдать 70 орлов и 30 решек из 100 подбрасываний? Мы будем использовать биномиальное распределение для количественной оценки вероятности. Биномиальное распределение использует априорную вероятность из бета-распределения (0,7) и количество экспериментов в качестве входных данных и выбирает количество орлов/решек из биномиального распределения.
Вероятность свидетельства: свидетельством являются наблюдаемые данные/результат эксперимента. Не зная, в чем состоит гипотеза, какова вероятность наблюдения за данными? Один из способов количественной оценки этого термина — вычислить P(H)*P(E|H) для каждой возможной гипотезы и взять сумму. Поскольку член доказательства находится в знаменателе, мы видим обратную зависимость между доказательством и апостериорной вероятностью. Другими словами, наличие высокой вероятности свидетельства ведет к малой апостериорной вероятности и наоборот. Высокая вероятность свидетельства отражает то, что альтернативные гипотезы так же совместимы с данными, как и текущая, поэтому мы не можем обновить наши предыдущие убеждения.

Кривая плотности вероятности биномиального распределения для 10 испытаний с априорной вероятностью, равной 0,7. Как видно, выпадение 7 орлов из 10 подбрасываний имеет наибольшую вероятность.

Моделирование документов и тем

Подумайте об этом так: я хочу создать новый документ, используя некоторые математические схемы. Имеет ли это хоть какой-то смысл? Если это так, как я могу это сделать? Идея LDA заключается в том, что каждый документ создается из смеси тем, и каждая из этих тем представляет собой распределение слов (Blei, 2003). Что вы можете сделать, так это случайным образом выбрать тему, взять слово из этой темы и поместить это слово в документ. Вы повторяете процесс, подбираете тему следующего слова, сэмплируете следующее слово, помещаете его в документ… и так далее. Процесс повторяется до завершения.

Следуя теореме Байеса, LDA узнает, как темы и документы представлены в следующей форме:

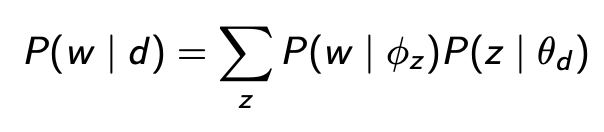
Блей и др. (2003). Скрытое распределение Дирихле.

Здесь стоит упомянуть две вещи:

Во-первых, документ состоит из смеси тем, где каждая тема z взята из полиномиального распределения z~Mult(θ) (Blei и др., 2003).

Назовем Theta (θ) распределение тем данного документа, то есть вероятность появления каждой темы в документе. Чтобы определить значение θ, мы выбираем тематическое распределение из распределения Дирихле. Если вы помните, что мы узнали из бета-распределения, каждая монета имеет разную вероятность выпадения орла. Точно так же каждый документ имеет разное распределение тем, поэтому мы хотим нарисовать распределения тем θ каждого документа из распределения Дирихле. Распределение Дирихле с использованием альфа / α - правильное знание / гипотеза в качестве входного параметра для создания тематического распределения θ, то есть θ ∼ Dir (α). Значение α в единицах Дирихле — это наша предварительная информация о смесях тем для этого документа. Затем мы используем θ, сгенерированное распределением Дирихле, в качестве параметров полиномиального распределения z∼Mult(θ) для генерации темы следующего слова в документе.

Во-вторых, каждая тема z состоит из смеси слов, где каждое слово взято из полиномиального распределения w~Mult(ϕ) (Blei и др., 2003).

Назовем phi (ϕ) распределением слов по каждой теме, т. е. вероятностью появления каждого слова в словаре в данной теме z. Чтобы определить значение ϕ, мы выбираем распределение слов по заданной теме из распределения Дирихле φz ∼ Dir(β), используя бета в качестве входного параметра β — априорную информацию о частоте слов в теме. Например, я могу использовать количество раз, когда каждое слово было назначено для данной темы в качестве значений β. Затем мы используем phi (ϕ), сгенерированный из Dir(β), в качестве параметра полиномиального распределения для выборки следующего слова в документе — при условии, что мы уже знали тему следующего слова.

Весь процесс генерации LDA для каждого документа выглядит следующим образом:

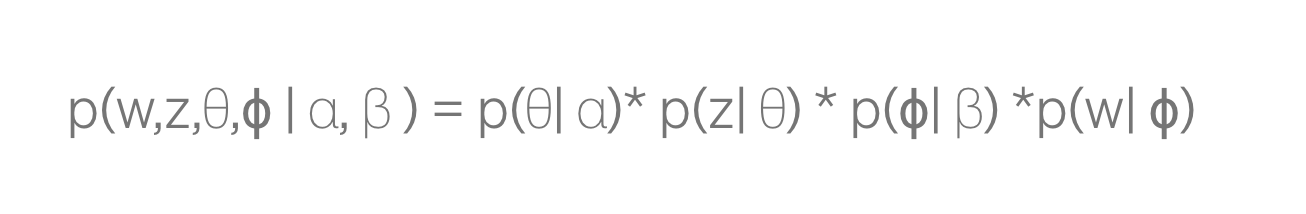
Подводя итог, первый шаг — получение тематических смесей документа — θ, сгенерированных из распределения Дирихле с параметром α. Это дает нам первый член. Тема z следующего слова берется из полиномиального распределения с параметром θ, что дает нам второй член. Затем вероятность появления каждого слова в документе ϕ определяется из распределения Дирихле с параметром β, что дает третий член p(ϕ|β). Как только мы узнаем тему следующего слова z, мы используем полиномиальное распределение, используя ϕ в качестве параметра, чтобы определить слово, которое дает нам последний термин.

Реализация Python с помощью Gensim

Набор данных

Реализация LDA python в этом посте использует набор данных, состоящий из корпуса текстов общих дебатов ООН. Он содержит все заявления, сделанные представителями каждой страны на общих дебатах ООН с 1970 по 2020 год. Набор данных является открытыми данными и доступен в Интернете.

Предварительная обработка данных

В рамках предварительной обработки мы будем использовать следующую конфигурацию:

Нижний регистр
Токенизировать (разделить документы на токены с помощью токенизации NLTK).
Лемматизация токенов (WordNetLemmatizer() из NLTK)
Удалить стоп-слова

Функции предварительной обработки текста.

def lemmatize_token(token):
    """
    lemmatize the token using nltk library
    Input: a single token
    Output: the lemmatization of the token
    """
    wordnet = WordNetLemmatizer()
    lemmatized_word = wordnet.lemmatize(token)
    return lemmatized_word
    
def preprocess_speech(speech):
    """
    This function does the preprocessing inlcuding lower case, tokenization, lemmatization and removing stopwords
    :param data:
    """
    # put all characters in lower case
    speech = speech.lower()

    # keep the tokens of the data
    tokens = nltk.word_tokenize(speech)

    # lemmatizing
    tokens = [lemmatize_token(token) for token in tokens]

    # remove stop words and non-alphabetic from all the text
    sw = nltk.corpus.stopwords.words("english")
    no_sw = []
    for w in tokens:
        if (w not in sw) and w.isalpha():
            no_sw.append(w)
    return no_sw

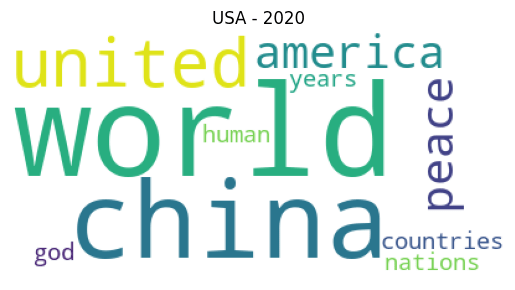
Пример некоторых атрибутов в наборе данных

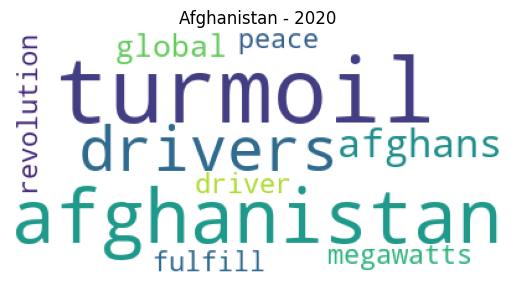
Пример 10 самых важных слов в речи США и Афганистана в 2020 году с использованием TF-IDF. Размер слова представляет вес/уровень важности.

Обучение модели LDA с использованием Gensim

Gensim — это бесплатная библиотека Python с открытым исходным кодом для обработки необработанных неструктурированных текстов и представления документов в виде семантических векторов. Gensim использует различные алгоритмы, такие как Word2Vec, FastText, LSI со скрытым семантическим индексированием, LDA со скрытым распределением Дирихле и т. д. Он будет обнаруживать семантическую структуру документов путем изучения статистических закономерностей совпадения в корпусе учебных документов.

Что касается параметров обучения, то прежде всего давайте обсудим слона в комнате: сколько тем в документах? На этот вопрос нет простого ответа, он зависит от ваших данных и ваших знаний о данных, а также от того, сколько тем вам действительно нужно. Я случайным образом использовал 10 тем, так как хотел иметь возможность интерпретировать и обозначать темы.

Параметры обучения модели LDA

texts = pd.eval(speeches['preprocessed_speech'], engine='python')
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]
lda_model = models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=10, update_every=1,
                                      chunksize =100000, passes=100, alpha='auto', eta='auto')

Параметр Chunksize определяет, сколько документов одновременно обрабатывается в алгоритме обучения. Пока фрагмент документов помещается в память, увеличение размера фрагмента ускорит обучение. Проходы контролируют, как часто мы обучаем модель на всем корпусе, что известно как эпохи. Альфа и эта — параметры, описанные в разделах 2.1 и 2.2. Параметр формы eta здесь соответствует beta.

В результате модели LDA, как показано ниже, давайте рассмотрим тему 0 в качестве примера. В нем говорится, что 0,015 — это вероятность того, что слово «нация» будет сгенерировано/появлено в документе. Это означает, что если вы рисуете выборку бесконечное количество раз, то слово «нация» будет выбрано в 0,015% случаев.

topic #0 (0.022): 0.015*"nation" + 0.013*"united" + 0.010*"country" + 0.010*"ha" + 0.008*"people" + 0.008*"international" + 0.007*"world" + 0.007*"peace" + 0.007*"development" + 0.006*"problem" 
topic #1 (0.151): 0.014*"country" + 0.014*"nation" + 0.012*"ha" + 0.011*"united" + 0.010*"people" + 0.010*"world" + 0.009*"africa" + 0.008*"international" + 0.008*"organization" + 0.007*"peace" 
topic #2 (0.028): 0.012*"security" + 0.011*"nation" + 0.009*"united" + 0.008*"country" + 0.008*"world" + 0.008*"international" + 0.007*"government" + 0.006*"state" + 0.005*"year" + 0.005*"assembly" 
topic #3 (0.010): 0.012*"austria" + 0.009*"united" + 0.008*"nation" + 0.008*"italy" + 0.007*"year" + 0.006*"international" + 0.006*"ha" + 0.005*"austrian" + 0.005*"two" + 0.005*"solution" 
topic #4 (0.006): 0.000*"united" + 0.000*"nation" + 0.000*"ha" + 0.000*"international" + 0.000*"people" + 0.000*"country" + 0.000*"world" + 0.000*"state" + 0.000*"peace" + 0.000*"organization" 
topic #5 (0.037): 0.037*"people" + 0.015*"state" + 0.012*"united" + 0.010*"imperialist" + 0.010*"struggle" + 0.009*"aggression" + 0.009*"ha" + 0.008*"american" + 0.008*"imperialism" + 0.008*"country" 
topic #6 (0.336): 0.017*"nation" + 0.016*"united" + 0.012*"ha" + 0.010*"international" + 0.009*"state" + 0.009*"world" + 0.008*"country" + 0.006*"organization" + 0.006*"peace" + 0.006*"development" 
topic #7 (0.010): 0.020*"israel" + 0.012*"security" + 0.012*"resolution" + 0.012*"state" + 0.011*"united" + 0.010*"territory" + 0.010*"peace" + 0.010*"council" + 0.007*"arab" + 0.007*"egypt" 
topic #8 (0.048): 0.016*"united" + 0.014*"state" + 0.011*"people" + 0.011*"nation" + 0.011*"country" + 0.009*"peace" + 0.008*"ha" + 0.008*"international" + 0.007*"republic" + 0.007*"arab" 
topic #9 (0.006): 0.000*"united" + 0.000*"nation" + 0.000*"country" + 0.000*"people" + 0.000*"ha" + 0.000*"international" + 0.000*"state" + 0.000*"peace" + 0.000*"problem" + 0.000*"organization"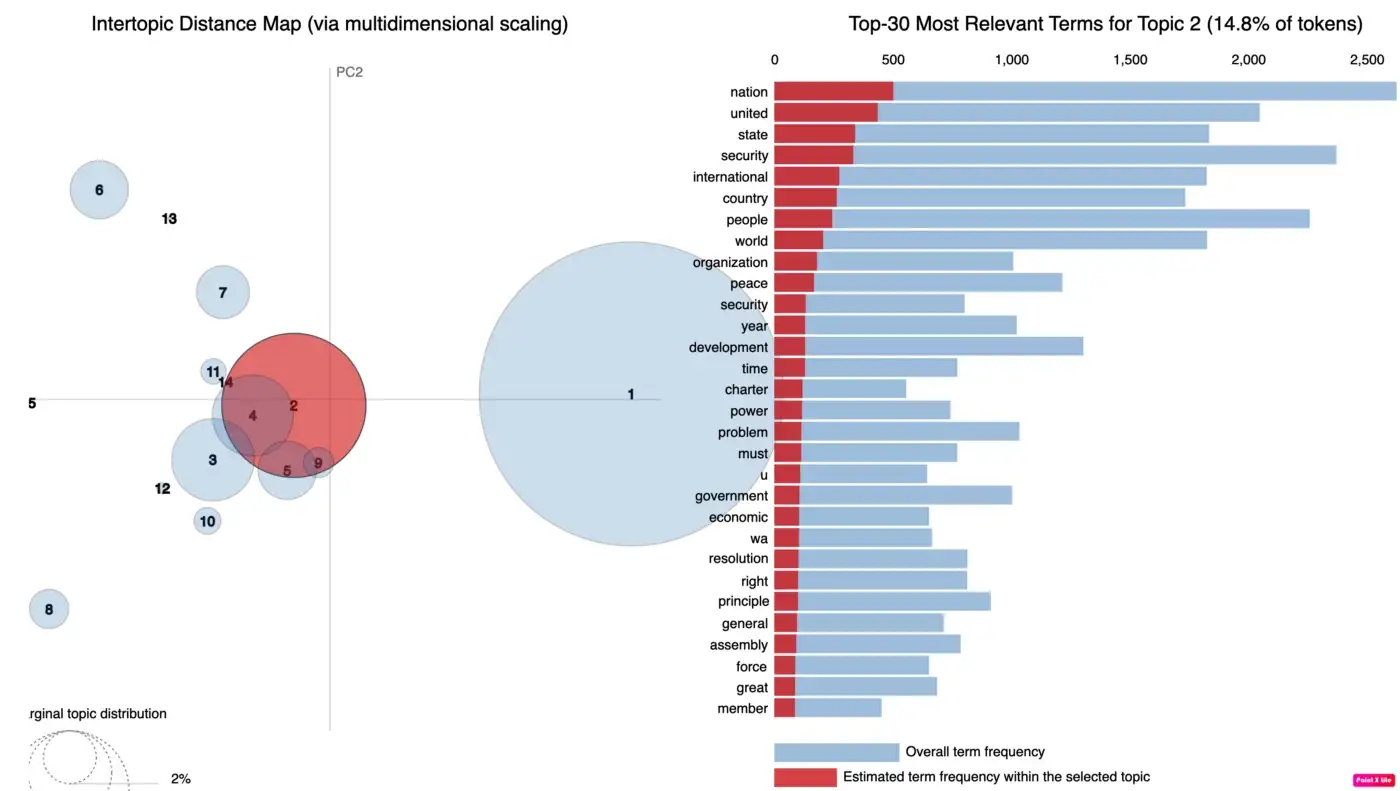

Каждый пузырь представляет собой тему. Синие полосы представляют собой общую частотность каждого слова в корпусе. Красные полосы показывают предполагаемое количество раз, когда данный термин был создан по данной теме. Слово с самой длинной красной полосой — это слово, которое чаще всего используется в речах, относящихся к этой теме. Нация, государство и безопасность, по-видимому, являются одними из наиболее часто используемых слов в этой латентной теме 2.

Качество тем

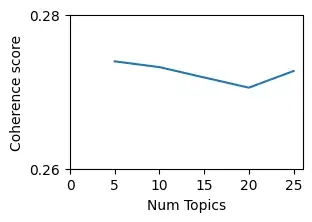
Создаваемые темы обычно используются для рассказа истории. Таким образом, темы хорошего качества — это те, которые легко интерпретируются людьми. Популярной метрикой для оценки качества темы является согласованность, где более высокие значения согласованности обычно соответствуют более интерпретируемым темам. Это означает, что мы можем использовать показатели согласованности тем для определения оптимального количества тем. Двумя популярными показателями согласованности являются оценки согласованности UMass и word2vec. UMass подсчитывает, как часто два слова в теме появляются в одном и том же документе по сравнению с тем, как часто они встречаются по отдельности. Наличие темы с такими словами, как United, Nations и States, будет иметь более низкую оценку связности, потому что, хотя United часто встречается вместе с Nations и States в одном и том же документе, Nations и States этого не делают. С другой стороны, оценки связности, основанные на word2vec, используют другой подход. Для каждой пары слов в теме word2vec векторизует каждое слово и вычисляет косинусное сходство. Оценка косинусного сходства говорит нам, являются ли два слова семантически похожими друг на друга.

Значения согласованности, соответствующие модели LDA с соответствующим количеством тем. Представляется, что выбор 5 тем, скорее всего, даст наилучший показатель согласованности/качества, даже несмотря на то, что различия в баллах для разного количества тем в этом случае незначительны.

Ограничения

Порядок не имеет значения: LDA обрабатывает документы как «мешок слов». Пакет слов означает, что вы просматриваете частоту слов в документе без учета порядка появления слов. Очевидно, что в этом процессе будет потеряна некоторая информация, но наша цель при тематическом моделировании состоит в том, чтобы иметь возможность для просмотра «большой картины» из большого количества документов. Альтернативный способ думать об этом: у меня есть словарь из 100 тысяч слов, используемых в 1 миллионе документов, затем я использую LDA для просмотра 500 тем.
Количество тем — это гиперпараметр, который должен быть установлен пользователем. На практике пользователь запускает LDA несколько раз с разным количеством тем и сравнивает оценки согласованности для каждой модели. Более высокие баллы согласованности обычно означают, что темы лучше интерпретируются людьми.
LDA не всегда хорошо работает с небольшими документами, такими как твиты и комментарии.
Темы, созданные LDA, не всегда поддаются интерпретации. На самом деле, исследования показали, что модели с наименьшей сложностью или логарифмической правдоподобием часто имеют менее поддающиеся интерпретации скрытые пространства (Chang и др. 2009).
Общие слова часто доминируют над каждой темой. На практике это означает удаление стоп-слов из каждого документа. Эти стоп-слова могут быть специфическими для каждого набора документов, и поэтому их необходимо создавать вручную.
Выбор правильной структуры для предварительного распределения. На практике такие пакеты, как Gensim, по умолчанию выбирают симметричный Дирихле. Это распространенный выбор, который в большинстве случаев не приводит к ухудшению извлечения темы (Wallach и др. 2009, Syed и др. 2018).
LDA не учитывает корреляции между темами. Например, «кулинария» и «диета» с большей вероятностью будут сосуществовать в одном и том же документе, а «кулинария» и «законы» — нет (Blei и др. 2005). В LDA предполагается, что темы независимы друг от друга из-за выбора использования распределения Дирихле в качестве априорного. Один из способов решить эту проблему — использовать коррелированные тематические модели вместо LDA, которые используют логистическое нормальное распределение вместо распределения Дирихле для построения тематических распределений.

#Python

1783

Войти на сайт