Замените списки Python и сделайте свой код быстрее

Каждый начинающий программист любит циклы for из-за их полезности и простоты понимания. Точно так же все любят массивы. Однако чаще всего мы начинаем использовать массивы для всего, даже не задумываясь. Мы ходим на занятия по структурам данных, но когда дело доходит до практики того, что мы узнали, мы не успеваем. Только недавно я поймал себя на том, что попал в эту ловушку. Я работал над задачей программирования, пытаясь заставить себя писать эффективный и быстрый код.
Мы можем сделать лучше!
В этом посте мы кратко рассмотрим словари и наборы в Python.
Мы (вновь) откроем для себя мощь этих структур данных в том, чтобы сделать операции с данными сверхбыстрыми в нашем коде. Мы узнаем, как хеш-таблицы могут привести к значительному улучшению алгоритмической производительности.
Но сначала нам нужно рассмотреть некоторые понятия.
Пора вернуться к истокам!
Назад к основам: хеш-таблицы
Структуры данных в языках программирования — это реализации абстрактных структур данных в информатике. Словари и наборы Python в основном представляют собой хэш-таблицу. Хеш-таблица является реализацией абстрактной структуры данных, называемой ассоциативным массивом, словарем или картой. Проще говоря, хеш-таблица — это сопоставление ключей со значениями. Имея ключ, можно запросить структуру данных, чтобы получить соответствующее значение.
Простым способом реализации этого может быть таблица прямых адресов или массив.
Таким образом, для ключа 1 мы будем хранить значение в позиции индекса массива 1.
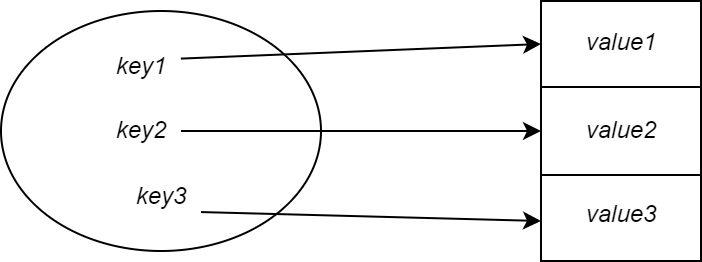
Каждый ключ просто сопоставляется со следующим слотом в массиве.
Однако есть одна проблема с этим подходом. Если ключей много, размер массива будет огромным. Это сделало бы невозможным хранение в памяти.
Решением этой проблемы является использование хеш-функции. Хэш-функция отвечает за сопоставление ключа со значением, хранящимся в хеш-таблице. Вы передаете ему ключ, и он выдает значение, называемое хэш-значением. Хэш-значение определяет, где в хеш-таблице хранить значение, соответствующее ключу. Другими словами, это индекс.
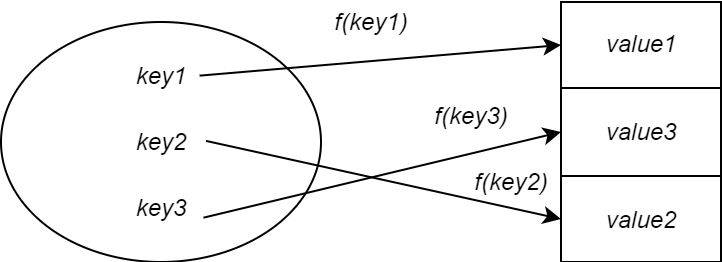
Теперь размер хеш-таблицы будет меньше размера таблицы прямых адресов. Это означает, что хеш-таблицу можно реализовать с точки зрения памяти. Однако это также означает, что два ключа могут сопоставляться одному и тому же значению.
Это называется коллизией хэшей и происходит, когда хеш-функция выводит одно и то же значение для двух разных ключей.
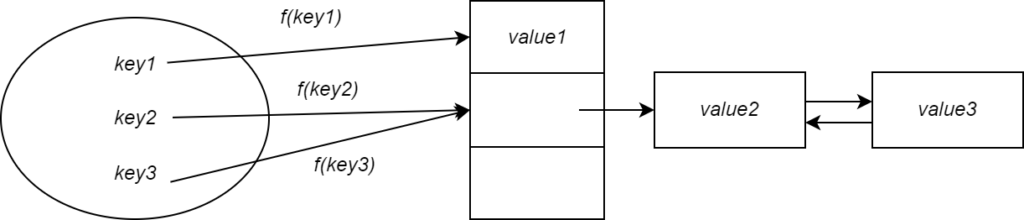
Чтобы решить эту проблему, мы можем сохранить значения в связанном списке, если два ключа хешируют одно и то же значение (см. рисунок выше). Любое последующее столкновение просто приведет к тому, что значение будет добавлено к связанному списку. Это называется разрешением коллизий путем связывания.
Теперь вы можете себе представить, если все ключи будут хешированы до одного и того же значения, все они будут добавлены в связанный список, а это означает, что производительность будет не лучше, чем при использовании списка!
Хеш-таблицы изменяются, если они становятся слишком полными. Порог называется коэффициентом загрузки и определяет соотношение занятых слотов к доступным слотам. Обычно, когда значение превышает размер 3/4 хэш-таблицы. Это гарантирует, что связанные списки никогда не станут слишком полными, и обеспечит обещанную среднюю производительность. Наконец, хеш-функции обычно выбираются таким образом, чтобы они равномерно распределяли ключи по слотам. Это означает, что вероятность столкновения с самого начала очень мала.
Здорово! Теперь давайте посмотрим на какую-нибудь большую нотацию O.
Назад к основам: O(1) против O(n)
Поиск элементов в массиве имеет среднюю временную сложность O(n), так как нам нужно линейно перемещаться по списку, чтобы найти элемент. Чем больше размер списка, тем больше времени потребуется для поиска элемента. Вы можете визуализировать это как линию стоящих людей, где вы начинаете с крайнего левого человека и спрашиваете, тот ли он, кого вы ищете.
Если нет, то спросите у человека рядом с ним и так далее. Вы можете себе представить, что поиск человека займет больше времени, если будет 1000 человек против 10.
Однако для хеш-таблицы средняя временная сложность поиска для случая O(1) - она постоянна. Неважно, сколько элементов вы храните, будь то миллион или 10, поиск элемента всегда будет занимать постоянную единицу времени. Другими словами, это было бы быстро для всех размеров ввода.
Вы можете представить себе группу стоящих людей и еще одного человека, который будет вашим помощником. Чтобы найти человека, вы просто спросите помощника, а не будете искать его в группе. Помощник мгновенно сообщит вам, где находится интересующий вас человек.
Вставка и удаление элементов также O(1).
Щелкните здесь, чтобы получить действительно хорошую шпаргалку по структурам данных и большому O.
Хорошо, теперь пора кодировать и увидеть хеш-таблицы в действии!
Код и тесты
Мы собираемся смоделировать следующую задачу:
- Список
L, содержащий элементы от 0 до 100 000 в отсортированном порядке. Третий последний индекс имеет случайно сгенерированное отрицательное значение в диапазоне от 0 до 100 000. - Список
R, содержащий элементы от 0 до 100 000 в отсортированном порядке.
Задача проста. Нам нужно найти значение в L, которое не появляется в R.
Я знаю, что есть более простые способы решения этой проблемы, но в целях обучения мы попробуем более сложный подход.
import time
import random
def solution(A, B):
for i in range(len(A)):
if A[i] not in B:
return A[i]
def solution2(A, B):
H=set(B)
for i in range(len(A)):
if A[i] not in H:
return A[i]
L = list(range(0, 100000))
L[-3] = -random.randint(0,100000)
R = list(range(0, 100000))
st=time.time()
solution(L, R)
print("elapsed 1", time.time() - st)
st=time.time()
solution2(L, R)
print("elapsed 2", time.time() - st)Функция solution является наивной реализацией решения. Мы перебираем L и для каждого элемента проверяем, существует ли он в списке R. Оператор in проверяет членство и сродни выполнению операции поиска. Если оно существует, мы просто возвращаем отрицательное целое число.
Истекшее время для этого решения составляет приблизительно 60 с.
Если мы проанализируем код функции solution, мы увидим, что временная сложность составляет O(n^2).
Это связано с тем, что для каждого элемента в L мы обходим R и проверяем принадлежность. Цикл for занимает O(n) при выполнении n шагов. Для каждого шага мы выполняем O(n) операций, так как нам нужно проверить каждый элемент в списке R и посмотреть, является ли он тем, который мы ищем.
Это дает O(n) * O(n) = O(n ^ 2)
Операция выполняется за квадратичное время. Затраченное время будет эквивалентно квадрату входного размера. Вы можете себе представить, как возведение в квадрат все больших и больших чисел дает постоянно возрастающие большие значения.
Что мы можем сделать, чтобы улучшить это?
Вместо обхода R для проверки членства мы можем реализовать R как хеш-таблицу вместо массива. Таким образом, временная сложность проверки членства будет O(1). В результате операция займет O(n)*O(1)=O(n).
Это линейно по размеру ввода! Таким образом, время, которое потребуется, будет пропорционально размеру ввода (в отличие от квадратичного).
Подождите, пока вы не увидите улучшения производительности!
Затраченное время solution2 0,011 с. Это улучшение более чем в 5000 раз!
Заключение и заключительные замечания
Таким образом, вы узнали мотивацию использования хеш-функций и хеш-таблиц. Мы кратко рассмотрели нотацию большого O для хеш-таблиц и сравнили ее с таковой для массивов. В довершение всего мы рассмотрели реализацию, которая использует хеш-таблицы для решения алгоритмической задачи в рекордно короткие сроки.
Как инженеры-программисты, мы должны знать, какой инструмент использовать в нужной ситуации, и не пытаться использовать методы грубой силы в каждом сценарии, с которым мы сталкиваемся.
Имея это в виду, нужно помнить несколько моментов.
Как и все остальное, хэш-таблицы не являются панацеей. Они не подходят для каждого варианта использования. Например, повторяющиеся элементы нельзя хранить в хеш-таблицах. Поэтому, если ваш вариант использования требует этого, вам лучше использовать массив. Точно так же хеш-таблицы не сортируются. Если для вашего варианта использования требуется отсортированная структура данных, хеш-таблицы не подходят. Наконец, нет встроенных функций для поиска максимального или минимального количества элементов в хеш-таблице. Наконец, временные сложности, упомянутые выше, являются средним случаем. Могут быть ситуации, когда возникает наихудший случай, когда хеш-таблицы будут работать так же, как массивы.
Надеюсь, вам понравилось содержание этого поста. До скорого.