Генерация синтетических данных с помощью Numpy и Scikit-Learn

В этом руководстве мы обсудим детали создания различных синтетических наборов данных с использованием библиотек Numpy и Scikit-learn. Мы увидим, как можно сгенерировать разные образцы из разных распределений с известными параметрами.
Мы также обсудим создание наборов данных для различных целей, таких как регрессия, классификация и кластеризация. В конце мы увидим, как мы можем создать набор данных, имитирующий распределение существующего набора данных.
Потребность в синтетических данных
В науке о данных синтетические данные играют очень важную роль. Это позволяет нам протестировать новый алгоритм в контролируемых условиях. Другими словами, мы можем генерировать данные, которые проверяют очень конкретное свойство или поведение нашего алгоритма.
Например, мы можем протестировать его производительность на сбалансированных и несбалансированных наборах данных, или мы можем оценить его производительность при разных уровнях шума. Делая это, мы можем установить базовый уровень производительности нашего алгоритма в различных сценариях.
Есть много других случаев, когда могут потребоваться синтетические данные. Например, получение реальных данных может быть трудным или дорогостоящим, либо в них может быть слишком мало точек данных. Другая причина - конфиденциальность, когда реальные данные не могут быть раскрыты.
Настройка
Прежде чем писать код для генерации синтетических данных, давайте импортируем необходимые библиотеки:
import numpy as np
# Needed for plotting
import matplotlib.colors
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Needed for generating classification, regression and clustering datasets
import sklearn.datasets as dt
# Needed for generating data from an existing dataset
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV
Затем вначале у нас будет несколько полезных переменных:
# Define the seed so that results can be reproduced
seed = 11
rand_state = 11
# Define the color maps for plots
color_map = plt.cm.get_cmap('RdYlBu')
color_map_discrete = matplotlib.colors.LinearSegmentedColormap.from_list("", ["red","cyan","magenta","blue"])
Создание одномерных выборок из известных распределений
Теперь мы поговорим о создании точек выборки из известных распределений в 1D.
Модуль random из numpy предлагает широкий спектр способов генерации случайных чисел, отобранных из известного распределения с фиксированным набором параметров. Для наших целей мы передадим seed (аналог python random.seed) в RandomState, и пока мы используем то же самое значение, мы получим те же самые числа.
Давайте определим список рассылки, такие как uniform, normal, exponential и т.д., список параметров и список цветов, чтобы мы могли визуально различать их:
rand = np.random.RandomState(seed)
dist_list = ['uniform','normal','exponential','lognormal','chisquare','beta']
param_list = ['-1,1','0,1','1','0,1','2','0.5,0.9']
colors_list = ['green','blue','yellow','cyan','magenta','pink']
Теперь мы упакуем их в подзаголовки Figure для визуализации и сгенерируем синтетические данные на основе этих распределений, параметров и назначим им соответствующие цвета.
Это делается с помощью функции eval(), которую мы используем для генерации выражения Python. Например, мы можем использовать rand.exponential(1, 5000) для генерации выборок из экспоненциального распределения масштаба 1 и размера 5000.
Здесь мы будем использовать наши dist_list, param_list и color_list для генерации этих вызовов:
fig,ax = plt.subplots(nrows=2, ncols=3,figsize=(12,7))
plt_ind_list = np.arange(6)+231
for dist, plt_ind, param, colors in zip(dist_list, plt_ind_list, param_list, colors_list):
x = eval('rand.'+dist+'('+param+',5000)')
plt.subplot(plt_ind)
plt.hist(x,bins=50,color=colors)
plt.title(dist)
fig.subplots_adjust(hspace=0.4,wspace=.3)
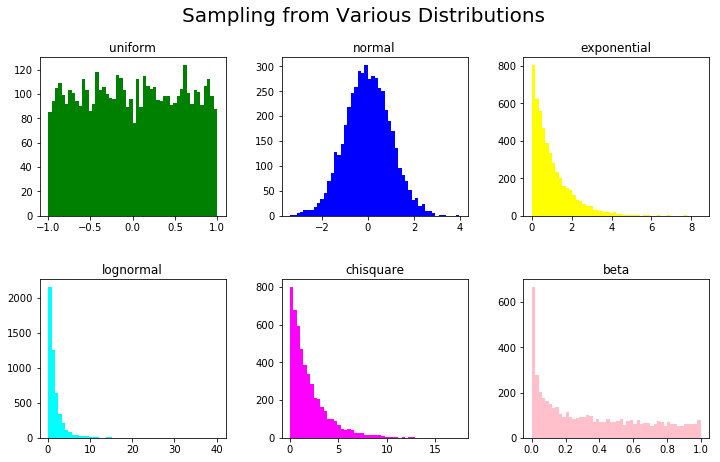
plt.suptitle('Sampling from Various Distributions',fontsize=20)
plt.show()
Это приводит к:
Синтетические данные для регрессии
В пакете sklearn.datasets есть функции для создания синтетических наборов данных для регрессии. Здесь мы обсуждаем линейные и нелинейные данные для регрессии.
Функция make_regression() возвращает набор точек ввода данных (регрессоров) вместе с их выходом (целью). Эту функцию можно настроить с помощью следующих параметров:
n_features- количество измерений / характеристик сгенерированных данныхnoise- стандартное отклонение гауссовского шумаn_samples- количество образцов
Переменная ответа представляет собой линейную комбинацию сгенерированного входного набора.
Переменная response - это то, что зависит от других переменных, в данном конкретном случае - от целевой функции, которую мы пытаемся предсказать, используя все другие входные функции.
В приведенном ниже коде синтетические данные были сгенерированы для разных уровней шума и состоят из двух входных функций и одной целевой переменной. Изменение цвета входных точек показывает изменение целевого значения, соответствующего точке данных. Данные создаются в 2D для лучшей визуализации, но данные большого размера могут быть созданы с помощью параметра n_features:
map_colors = plt.cm.get_cmap('RdYlBu')
fig,ax = plt.subplots(nrows=2, ncols=3,figsize=(16,7))
plt_ind_list = np.arange(6)+231
for noise,plt_ind in zip([0,0.1,1,10,100,1000],plt_ind_list):
x,y = dt.make_regression(n_samples=1000,
n_features=2,
noise=noise,
random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x[:,0],
x[:,1],
c=y,
vmin=min(y),
vmax=max(y),
s=35,
cmap=color_map)
plt.title('noise: '+str(noise))
plt.colorbar(my_scatter_plot)
fig.subplots_adjust(hspace=0.3,wspace=.3)
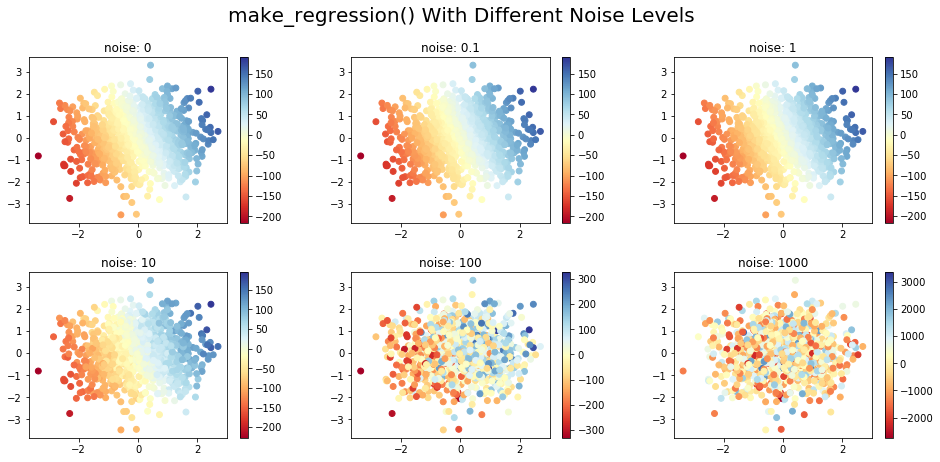
plt.suptitle('make_regression() With Different Noise Levels',fontsize=20)
plt.show()
Здесь мы создали пул из 1000 образцов с двумя функциями (классами). В зависимости от уровня шума (0..1000) мы можем увидеть, насколько сгенерированные данные существенно различаются на диаграмме рассеяния:
Семейство функций make_friedman
Существует три версии функции make_friedman?() (замените на ?значение из {1,2,3}).
Эти функции генерируют целевую переменную, используя нелинейную комбинацию входных переменных, как подробно описано ниже:
make_friedman1(): Аргумент n_features этой функции должен быть не менее 5, следовательно, минимальное количество входных измерений 5. Здесь цель задается:
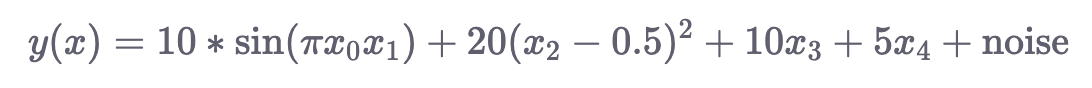
make_friedman2(): Сгенерированные данные имеют 4 входных измерения. Переменная response задается следующим образом:
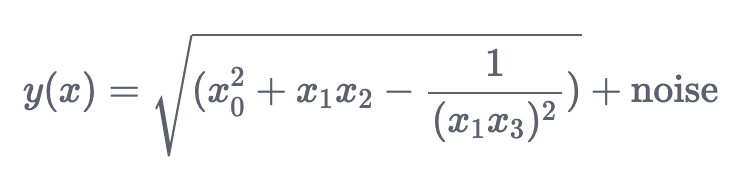
make_friedman3(): Сгенерированные данные в этом случае также имеют 4 измерения. Выходная переменная определяется следующим образом:
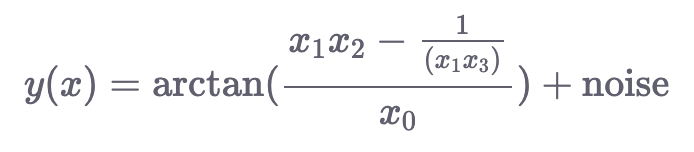
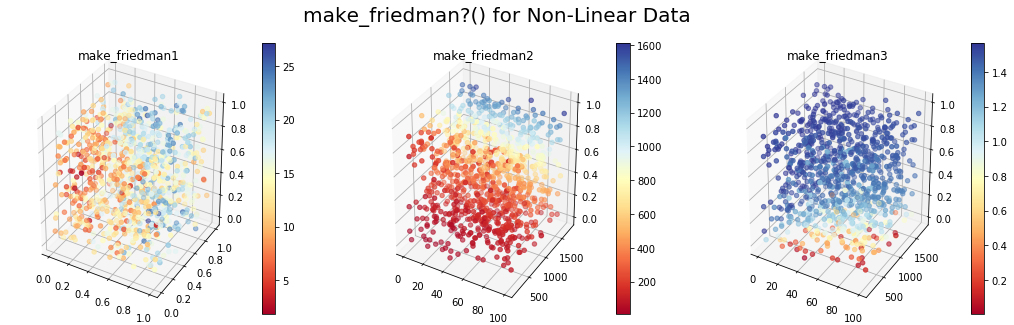
Приведенный ниже код генерирует наборы данных с использованием этих функций и отображает первые три функции в 3D, причем цвета меняются в зависимости от целевой переменной:
fig = plt.figure(figsize=(18,5))
x,y = dt.make_friedman1(n_samples=1000,n_features=5,random_state=rand_state)
ax = fig.add_subplot(131, projection='3d')
my_scatter_plot = ax.scatter(x[:,0], x[:,1],x[:,2], c=y, cmap=color_map)
fig.colorbar(my_scatter_plot)
plt.title('make_friedman1')
x,y = dt.make_friedman2(n_samples=1000,random_state=rand_state)
ax = fig.add_subplot(132, projection='3d')
my_scatter_plot = ax.scatter(x[:,0], x[:,1],x[:,2], c=y, cmap=color_map)
fig.colorbar(my_scatter_plot)
plt.title('make_friedman2')
x,y = dt.make_friedman3(n_samples=1000,random_state=rand_state)
ax = fig.add_subplot(133, projection='3d')
my_scatter_plot = ax.scatter(x[:,0], x[:,1],x[:,2], c=y, cmap=color_map)
fig.colorbar(my_scatter_plot)
plt.suptitle('make_friedman?() for Non-Linear Data',fontsize=20)
plt.title('make_friedman3')
plt.show()
Синтетические данные для классификации
Scikit-learn имеет простые и легкие в использовании функции для создания наборов данных для классификации в модуле sklearn.dataset. Давайте рассмотрим пару примеров.
make_classification() для задач классификации n-класса
Для задач классификации n-класса функция make_classification() имеет несколько вариантов:
class_sep: Указывает, должны ли различные классы быть более разбросанными и легче различатьn_features: Количество функцийn_redundant: Количество избыточных функцийn_repeated: Количество повторяющихся функцийn_classes: Общее количество классов
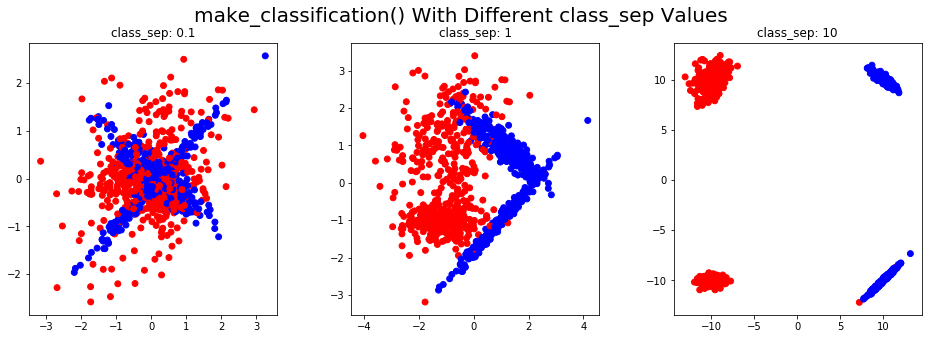
Создадим набор данных классификации для двумерных входных данных. У нас будут разные значения class_sep для задачи двоичной классификации. Точки одного цвета относятся к одному классу. Стоит отметить, что эта функция также может генерировать несбалансированные классы:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for class_sep,plt_ind in zip([0.1,1,10],plt_ind_list):
x,y = dt.make_classification(n_samples=1000,
n_features=2,
n_repeated=0,
class_sep=class_sep,
n_redundant=0,
random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x[:,0],
x[:,1],
c=y,
vmin=min(y),
vmax=max(y),
s=35,
cmap=color_map_discrete)
plt.title('class_sep: '+str(class_sep))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_classification() With Different class_sep Values',fontsize=20)
plt.show()
make_multilabel_classification() для задач классификации Multi-Label
Функция make_multilabel_classification() генерирует данные для задач классификации с несколькими метками. У него есть различные опции, наиболее заметная из которых n_label - установка среднего количества меток на точку данных.
Давайте рассмотрим 4-х классную задачу с несколькими метками, при которой целевой вектор меток преобразуется в одно значение для визуализации. Точки раскрашены в соответствии с десятичным представлением двоичного вектора меток. Код поможет вам увидеть, как использование другого значения для n_label меняет классификацию сгенерированной точки данных:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for label,plt_ind in zip([2,3,4],plt_ind_list):
x,y = dt.make_multilabel_classification(n_samples=1000,
n_features=2,
n_labels=label,
n_classes=4,
random_state=rand_state)
target = np.sum(y*[8,4,2,1],axis=1)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x[:,0],
x[:,1],
c=target,
vmin=min(target),
vmax=max(target),
cmap=color_map)
plt.title('n_labels: '+str(label))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_multilabel_classification() With Different n_labels Values',fontsize=20)
plt.show()
Синтетические данные для кластеризации
Для кластеризации sklearn.datasets предлагается несколько вариантов. Здесь мы будем охватывать функции make_blobs() и make_circles().
make_blobs()
Функция make_blobs() генерирует данные из изотропных гауссовских распределений. В качестве аргумента можно указать количество функций, количество центров и стандартное отклонение каждого кластера.
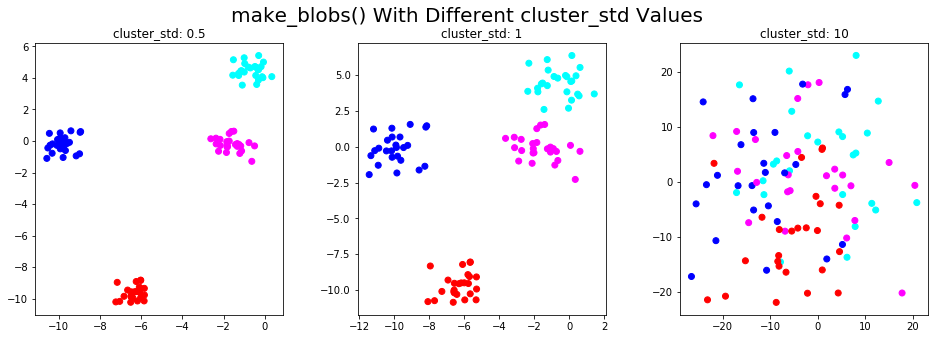
Здесь мы проиллюстрируем эту функцию в 2D и покажем, как точки данных меняются с разными значениями параметра cluster_std:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for std,plt_ind in zip([0.5,1,10],plt_ind_list):
x, label = dt.make_blobs(n_features=2,
centers=4,
cluster_std=std,
random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x[:,0],
x[:,1],
c=label,
vmin=min(label),
vmax=max(label),
cmap=color_map_discrete)
plt.title('cluster_std: '+str(std))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_blobs() With Different cluster_std Values',fontsize=20)
plt.show()
make_circles()
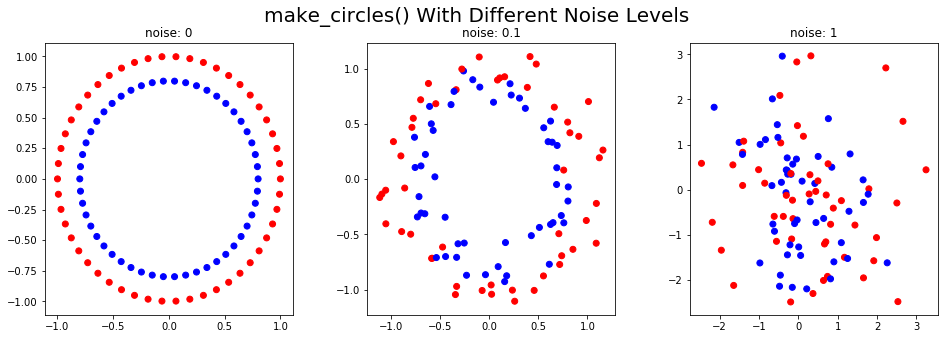
Функция make_circles() генерирует две концентрических окружности с тем же центром, один внутри другого.
Используя параметр шума, к сгенерированным данным можно добавить искажения. Этот тип данных полезен для оценки алгоритмов кластеризации на основе сходства. В приведенном ниже коде показаны синтетические данные, сгенерированные при разных уровнях шума:
fig,ax = plt.subplots(nrows=1, ncols=3,figsize=(16,5))
plt_ind_list = np.arange(3)+131
for noise,plt_ind in zip([0,0.1,1],plt_ind_list):
x, label = dt.make_circles(noise=noise,random_state=rand_state)
plt.subplot(plt_ind)
my_scatter_plot = plt.scatter(x[:,0],
x[:,1],
c=label,
vmin=min(label),
vmax=max(label),
cmap=color_map_discrete)
plt.title('noise: '+str(noise))
fig.subplots_adjust(hspace=0.3,wspace=.3)
plt.suptitle('make_circles() With Different Noise Levels',fontsize=20)
plt.show()
Генерация выборок, полученных из входного набора данных
Есть много способов создания дополнительных выборок данных из существующего набора данных. Здесь мы проиллюстрируем очень простой метод, который сначала оценивает плотность данных ядра с использованием гауссова ядра, а затем генерирует дополнительные выборки из этого распределения.
Чтобы визуализировать только что сгенерированные образцы, давайте посмотрим на набор данных Olivetti Faces, который можно получить через sklearn.datasets.fetch_olivetti_faces(). В наборе данных есть 10 разных изображений лиц 40 разных людей.
Вот что мы будем делать:
- Получить данные о лицах
- Сгенерируйте модель плотности ядра из данных
- Используйте плотность ядра для генерации новых выборок данных
- Покажите оригинальные и синтетические лица.
# Fetch the dataset and store in X
faces = dt.fetch_olivetti_faces()
X= faces.data
# Fit a kernel density model using GridSearchCV to determine the best parameter for bandwidth
bandwidth_params = {'bandwidth': np.arange(0.01,1,0.05)}
grid_search = GridSearchCV(KernelDensity(), bandwidth_params)
grid_search.fit(X)
kde = grid_search.best_estimator_
# Generate/sample 8 new faces from this dataset
new_faces = kde.sample(8, random_state=rand_state)
# Show a sample of 8 original face images and 8 generated faces derived from the faces dataset
fig,ax = plt.subplots(nrows=2, ncols=8,figsize=(18,6),subplot_kw=dict(xticks=[], yticks=[]))
for i in np.arange(8):
ax[0,i].imshow(X[10*i,:].reshape(64,64),cmap=plt.cm.gray)
ax[1,i].imshow(new_faces[i,:].reshape(64,64),cmap=plt.cm.gray)
ax[0,3].set_title('Original Data',fontsize=20)
ax[1,3].set_title('Synthetic Data',fontsize=20)
fig.subplots_adjust(wspace=.1)
plt.show()

Показанные здесь исходные лица представляют собой образцы 8 лиц, выбранных из 400 изображений, чтобы получить представление о том, как выглядит исходный набор данных. Мы можем сгенерировать столько новых точек данных, сколько захотим, используя функцию sample().
В этом примере было создано 8 новых образцов. Обратите внимание, что синтетические лица, показанные здесь, не обязательно соответствуют лицу человека, показанного над ним.
Выводы
В этой статье мы познакомились с несколькими методами генерации синтетических наборов данных для различных задач. Синтетические наборы данных помогают нам оценивать наши алгоритмы в контролируемых условиях и устанавливать базовый уровень для показателей производительности.
Python имеет широкий спектр функций, которые можно использовать для создания искусственных данных. Важно понимать, какие функции и API можно использовать для ваших конкретных требований.