Тесты статистической проверки принадлежности нормальному распределению Python
Нормальное распределение — это тип распределения, который, вероятно, наиболее часто упоминается и используется статистиками. Вероятно, это первое распределение, которое вы будете изучать на уроках статистики. Что это за раздача, собственно? Его также называют распределением Гаусса, и оно представляет собой распределение случайно сгенерированных переменных, напоминающее колоколообразную кривую. Он характеризуется средним значением и стандартным отклонением. Эти два значения определяют конкретную форму распределения, хотя общая колоколообразная форма не изменится так сильно. Например, небольшое стандартное отклонение относительно среднего дает крутой график, а большое стандартное отклонение дает плоский график.
Какое отношение это распределение имеет к нашим проектам по науке о данных? Это важно, потому что многие статистические тесты, модели машинного обучения и статистические теории требуют, чтобы переменная или переменные следовали этому распределению. Следовательно, нам нужны способы убедиться, что переменные или выборки следуют нормальному распределению. В этой статье я дам вам исчерпывающий обзор большинства тестов для проверки нормальности и их реализации на Python.
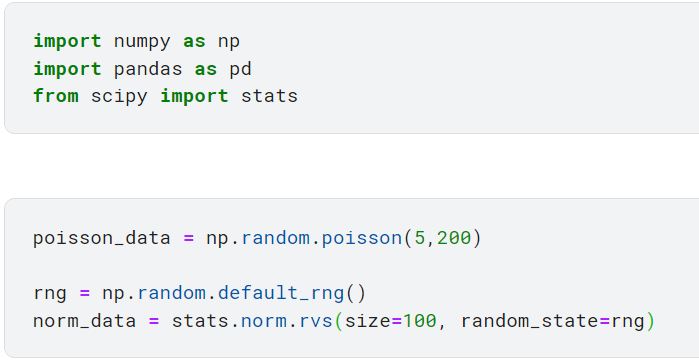
Прежде чем мы углубимся в каждый тест на нормальность, давайте сначала создадим поддельные образцы, которые будут использоваться для наших фрагментов кода. Одна выборка будет взята из нормального распределения, а другая будет взята из распределения Пуассона, которое является еще одним типом распределения, обычно используемым для подсчета данных (например, числа людей).
1. Тест Шапиро-Уилка
Этот тест, вероятно, является наиболее распространенным тестом на нормальность, который используют люди. Он вычисляет статистику W, которая проверяет, происходят ли случайные выборки из нормального распределения. Статистику W можно определить следующим образом:
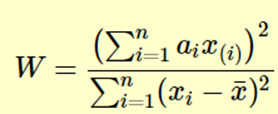
где x(i) — значения упорядоченной выборки.
H0 (нулевая гипотеза): выборка исходит из нормального распределения.
Xа (Альтернативная гипотеза): выборка не соответствует нормальному распределению.
Этот тест является параметрическим в том смысле, что существует предположение, которое должно быть выполнено для запуска этого теста. Это предположение состоит в том, что наблюдения в каждой выборке независимы и одинаково распределены (iid).
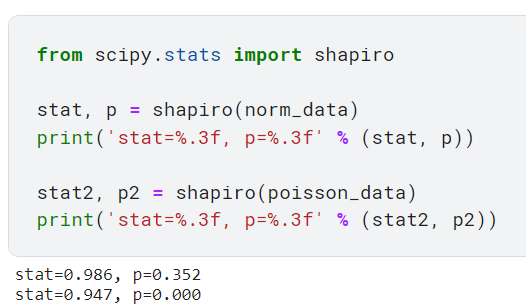
Если значение W мало, это свидетельствует об отклонении от нормы. Для этого теста класс scipy.stats предоставляет модуль под названием shapiro.
Следует также отметить, что если количество выборок превышает 5000, статистика теста W является точной, но значение p может быть неточным, согласно документации scipy.
2. Тест Колмогорова-Смирнова
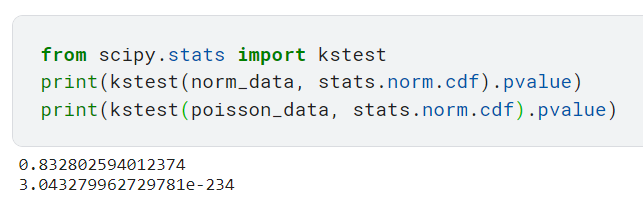
В отличие от теста Шапиро-Уилка, этот тест проверяет, насколько хорошо распределение выборочных данных соответствует некоторому теоретическому распределению, которое не ограничивается только нормальным распределением. Мы используем модуль kstest из класса scipy.stats.
Обратите внимание, что нулевая и альтернативная гипотезы меняются в зависимости от того, как мы определяем альтернативный аргумент в scipy.stats.kstest. Значение по умолчанию для этого аргумента — «двусторонний».
двусторонний (по умолчанию): нулевая гипотеза состоит в том, что два распределения идентичны, F(x)=G(x) для всех x; альтернатива в том, что они не идентичны.
меньше: нулевая гипотеза состоит в том, что F(x) >= G(x) для всех x; альтернатива состоит в том, что F (x) < G (x) по крайней мере для одного x.
больше: нулевая гипотеза состоит в том, что F(x) <= G(x) для всех x; альтернатива состоит в том, что F(x) > G(x) по крайней мере для одного x.
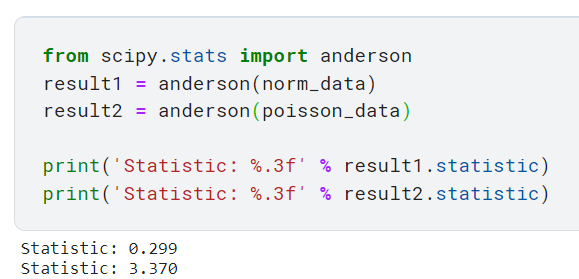
3. Тест Андерсона-Дарлинга (тест AD)
Этот тест проверяет, взят ли образец из определенного дистрибутива. На самом деле это модифицированная версия теста Колмогорова-Смирнова из предыдущего раздела. Распределения, с которыми этот тест может сравнить нарисованную выборку, — это нормальное, экспоненциальное, логистическое распределение и распределение Гамбеля. Некоторые люди могут быть незнакомы с распределением Гамбеля, но это тип распределения экстремальных значений, при котором распределение смещено влево (т. е. хвост длиннее вправо, а большинство точек данных сгруппировано слева).
Нулевая и альтернативная гипотезы следующие:
H0: Выборка берется из совокупности с определенным распределением.
Xа: Данные не поступают из определенного дистрибутива.
Класс scipy.stats предлагает модуль с именем anderson, который позволяет выполнять этот тест. Что интересно в этом модуле, так это то, что он предоставляет уже определенные критические значения для следующих уровней значимости для каждого вида распределения.
Hормальный / Экспоненциальный
→ 15%, 10%, 5%, 2,5%, 1%
Логистика
→ 25%, 10%, 5%, 2,5%, 1%, 0,5%
Гамбель
→ 25%, 10%, 5%, 2,5%, 1%
4. Тест Лиллиефорса
Это еще один тест на нормальность, основанный на тесте Колмогорова-Смирнова. Это специально используется для проверки нулевой гипотезы о том, что выборка происходит из нормально (или экспоненциально) распределенной совокупности, для которой ожидаемое значение и дисперсия распределения неизвестны.
Пакет statsmodels раньше предлагал модуль statsmodels.stats.diagnostic.lilliefors(), но, похоже, он устарел или испытывает некоторые проблемы.
Поскольку это тест, основанный на Колмогорове-Смирнове, возвращается также статистика Колмогорова-Смирнова и значение p.
5. Критерий К-квадрата Д'Агостино
Этот тест сочетает в себе тест на перекос и тест на эксцесс для проверки нормальности. Перекос — это значение, которое говорит нам, насколько распределение сосредоточено влево или вправо. Другими словами, это мера асимметрии распределения. Эксцесс похож на перекос, но отличается тем, что он говорит нам, какая часть распределения сосредоточена в хвосте. Объединяя эти две метрики, критерий Д'Агостино К-квадрат призван обеспечить большую надежность. Фактическая статистика, возвращаемая этим тестом, равна s² + k², где s — это z-оценка, возвращаемая проверкой перекоса, а k — z-оценка, возвращаемая проверкой эксцесса.
Нулевая и альтернативная гипотезы следующие:
H0: выборка исходит из нормального распределения.
Xа: Образец не из нормального распределения.

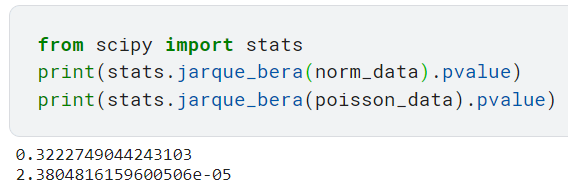
6. Тест Харке-Бера
Этот тест проверяет, взята ли выборка из нормального распределения, сосредоточив внимание на асимметрии и эксцессе выборки и соответствуют ли они таковым нормального распределения.
Он возвращает неотрицательную статистику, и если она далека от нуля, это говорит нам о том, что данные не следуют нормальному распределению. Обратите внимание, что этот тест работает только для достаточно большого количества выборок данных (> 2000), поскольку статистика теста асимптотически имеет распределение хи-квадрат с 2 степенями свободы, согласно документации Scipy.
Некоторые другие тесты на нормальность, которые не используются так часто, как приведенные выше:
Тест Мартинеса-Иглевича
Чи Пирсона — квадратичный критерий нормальности
Тест нормальности Шапиро — Франции
Критерий нормальности Крамера — фон Мизеса
Если вы пользователь R, есть несколько пакетов, которые позволяют вам выполнять те же тесты, что и выше.
Вывод
Несмотря на то, что существует много типов тестов нормальности, перечисленных выше, убедитесь, что вы понимаете, что происходит в фоновом режиме (например, математические формулировки), когда каждый из тестов является лучшим для использования (например, размер выборки) и его гибкость (например, позволяет нам проверить, следуют ли наши образцы другому типу распределения, отличному от нормального распределения)! Таким образом, вы сможете определить, какой тест использовать для вашей конкретной цели и случая.